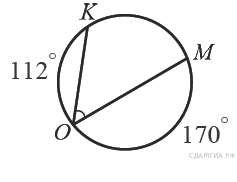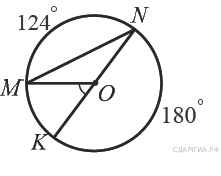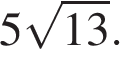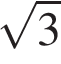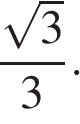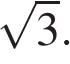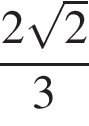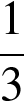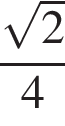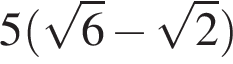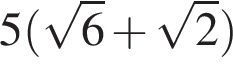Задание 17 номер 169850 - Большой телефонный справочник предприятий

Огэ по математике 169850

Задание 17 № 169847

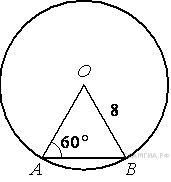
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на.

Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:

Задание 17 № 169848

Периметр равностороннего треугольника равен 30. Найдите его площадь, Делённую на.

Так как в равностороннем треугольнике все стороны равны, то сторона данного треугольника равна 10. Угол равностороннего треугольника равен 60°. Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:

Задание 17 № 169849

Высота равностороннего треугольника равна 10. Найдите его площадь, Делённую на

Высота равностороннего треугольника равна Таким образом, сторона равностороннего треугольника равна Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:

В открытом банке иррациональный ответ.

Задание 17 № 169850

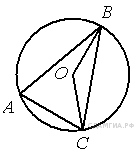
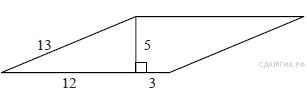
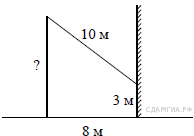
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, Делённую на

Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:

В открытом банке иррациональный ответ.

Задание 17 № 169851

Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.

Так как боковая сторона равнобедренного треугольника равна 5, его основание равно 6, а полупериметр: по формуле Герона имеем:

Приведём другое решение.

Найдя основание и боковые стороны равнобедренного треугольника, находим по теореме Пифагора высоту, она равна 4. Далее по формуле площади треугольника, находим, что она равна 12.

Задание 17 № 169850

Задание 17 № 169851

Периметр равнобедренного треугольника равен 16, а боковая сторона 5.

Oge. sdamgia. ru

29.04.2020 14:58:34

2020-04-29 14:58:34

Источники:

Https://oge. sdamgia. ru/test? theme=39

Презентация по геометрии по подготовке к экзамену (№ 16). » /> » /> .keyword { color: red; } Огэ по математике 169850

Презентация по геометрии по подготовке к экзамену (№ 16)

Презентация по геометрии по подготовке к экзамену (№ 16).

презентация по геометрии по подготовке к экзамену (№ 16).

Для выработки умений решать задачи по геометрии второй части в девятом классе необходимо, чтобы ученики хорошо знали теоретический материал, что обычно у школьников западает, так вот для этого можно составить презентации с разбором сложных задач с комментированием теоретических вопросов и когда они часто проговаривают их, знания остаются в памяти.

ГИА — 2016 Открытый банк заданий по математике

гиа - 2016 открытый банк заданий по математике

Открытый банк заданий
По математике.

Прямоугольный треугольник. Равносторонний треугольник

прямоугольный треугольник. равносторонний треугольник

Круг. Круговой сектор.

Вашему вниманию представлены тридцать шесть
Прототипов Задачи № 16
Открытого банка заданий по математике. ГИА – 2016.

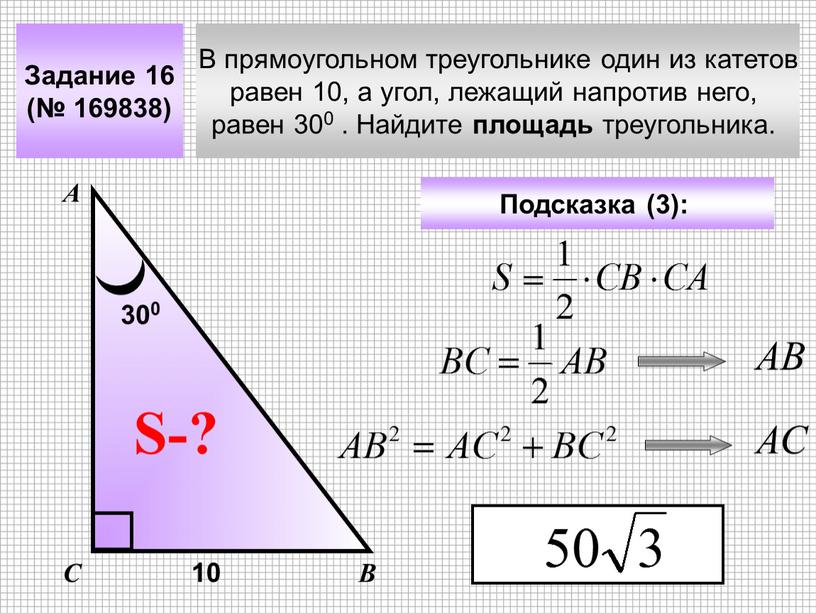
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 300

в прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 300

В прямоугольном треугольнике один из катетов
Равен 10, а угол, лежащий напротив него,
Равен 300 . Найдите Площадь треугольника.

Открытый банк заданий по математике.

Znanio. ru

26.07.2018 11:27:15

2018-07-26 11:27:15

Источники:

Https://znanio. ru/media/prezentatsiya_po_geometrii_po_podgotovke_k_ekzamenu__16-40752

Материал по математике для подготовки к ОГЭ » /> » /> .keyword { color: red; } Огэ по математике 169850

Материал по математике для подготовки к ОГЭ

нажмите, чтобы узнать подробности

Весь материал разбит на темы, включенные в КИМы ОГЭ-9 по математике.

Просмотр содержимого документа
«10Okrug_ixElementu»

Окружность, круг и их элементы

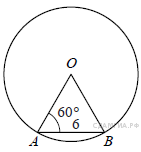
1. B 7 № 90. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

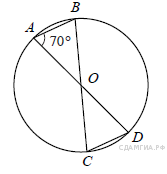
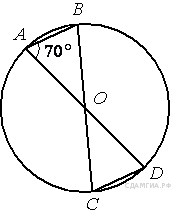
2. B 7 № 116. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.

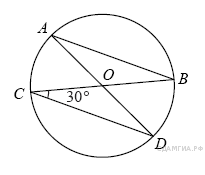
3. B 7 № 142. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

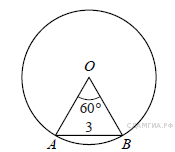
4. B 7 № 194. Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.

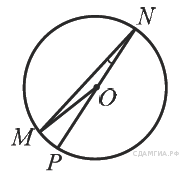
5. B 7 № 311319. Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

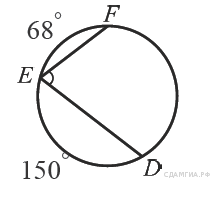
6. B 7 № 311331. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

7. B 7 № 311342. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.

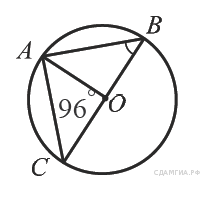
8. B 7 № 311354. Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера ∠AOC равна 96°.

9. B 7 № 311374. Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.

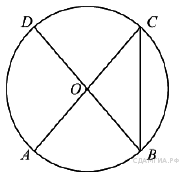
10. B 7 № 311386. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 112°. Найдите вписанный угол ACB. Ответ дайте в градусах.

11. B 7 № 311398. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.

12. B 7 № 311410. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

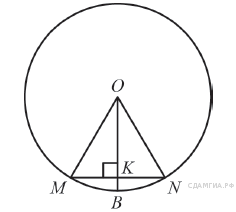
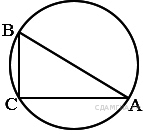
13. B 7 № 311464. Радиус OB окружности с центром в точке O пересекает хорду MN в её середине — точке K. Найдите длину хорды MN, если KB = 1 см, а радиус окружности равен 13 см.

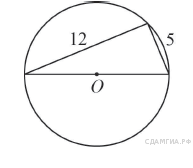
14. B 7 № 311479. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

15. B 7 № 311483. Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

16. B 7 № 311487. Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.

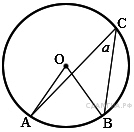
17. B 7 № 311488. Найдите величину (в градусах) вписанного угла Α, опирающегося на хорду AB, равную радиусу окружности.

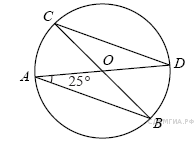
18. B 7 № 311494. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.

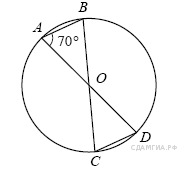
19. B 7 № 311497. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.

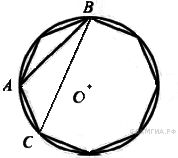
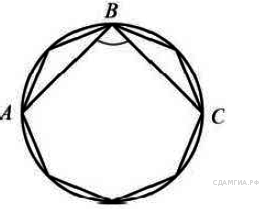
20. B 7 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

21. B 7 № 311507. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

22. B 7 № 311510. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.

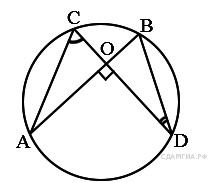
23. B 7 № 311517. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.

24. B 7 № 311523. Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.

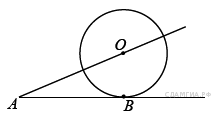
25. B 7 № 311681. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

26. B 7 № 311760. В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.

27. B 7 № 311816. В треугольнике ABC угол C равен 90°, BC = 20, = 0,5. Найдите AC.

28. B 7 № 311848. В треугольнике ABC угол C равен 90°, BC = 18, tgA = 3. Найдите AC.

29. B 7 № 311912.

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.

30. B 7 № 311956.

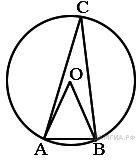
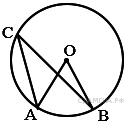
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.

31. B 7 № 314807. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.

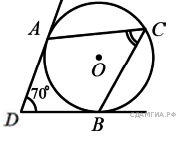
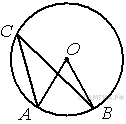
32. B 7 № 314811. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

33. B 7 № 314850. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70° . Найдите величину угла OCD.

34. B 7 № 314873. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах).

35. B 7 № 314956. Точка О — центр окружности, ∠BAC = 70° (см. рисунок). Найдите величину угла BOC (в градусах).

36. B 7 № 315006. Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.

37. B 7 № 316230. В треугольнике ABC угол C равен 90° , BC = 20, tgA = 0,5. Найдите AC.

38. B 7 № 316257. В треугольнике ABC угол C равен 90°, BC = 18, tgA = 3. Найдите AC.

39. B 7 № 316320. В треугольнике ABC угол C равен 90°, AC = 12 , tgA = 1,5. Найдите BC.

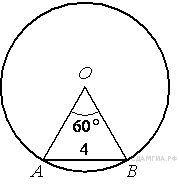
40. B 7 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

41. B 7 № 316372. Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Просмотр содержимого документа
«11PlogadiFigur»

Площади фигур

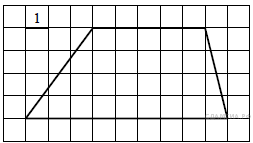
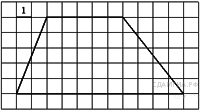
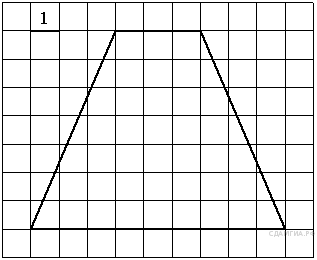
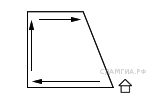
1. B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.

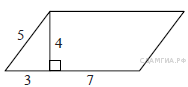
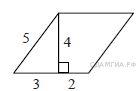
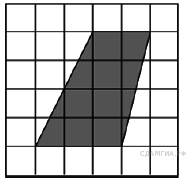
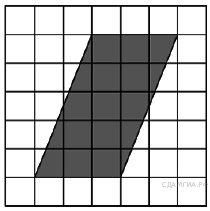
2. B 8 № 65. Найдите площадь параллелограмма, изображённого на рисунке.

3. B 8 № 91. Найдите площадь параллелограмма, изображённого на рисунке.

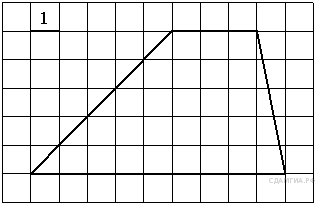
4. B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.

5. B 8 № 143. Найдите площадь трапеции, изображённой на рисунке.

6. B 8 № 195. Найдите площадь параллелограмма, изображённого на рисунке.

7. B 8 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.

8. B 8 № 169841. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.

9. B 8 № 169847. Сторона равностороннего треугольника равна 10. Найдите его площадь, Делённую на.

10. B 8 № 169848. Периметр равностороннего треугольника равен 30. Найдите его площадь, Делённую на.

11. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь, Делённую на

12. B 8 № 169850. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, Делённую на

13. B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.

14. B 8 № 169852. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника.

15. B 8 № 169853. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.

16. B 8 № 169854. В треугольнике одна из сторон равна 10, другая равна, а угол между ними равен 60°. Найдите площадь треугольника.

17. B 8 № 169855. В треугольнике одна из сторон равна 10, другая равна, а угол между ними равен 45°. Найдите площадь треугольника.

18. B 8 № 169856. В треугольнике одна из сторон равна 10, другая равна, а угол между ними равен 120°. Найдите площадь треугольника.

19. B 8 № 169857. В треугольнике одна из сторон равна 10, другая равна, а угол между ними равен 135°. Найдите площадь треугольника.

20. B 8 № 169858. В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.

21. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен. Найдите площадь треугольника.

22. B 8 № 169860. В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен. Найдите площадь треугольника.

23. B 8 № 169862. Сторона квадрата равна 10. Найдите его площадь.

24. B 8 № 169863. Периметр квадрата равен 40. Найдите площадь квадрата.

25. B 8 № 169864. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.

26. B 8 № 169865. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.

27. B 8 № 169866. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.

28. B 8 № 169867. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, Делённую на .

29. B 8 № 169868. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.

30. B 8 № 169869. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.

31. B 8 № 169870. Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба, Делённую на .

32. B 8 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, Делённую на .

33. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен. Найдите площадь ромба.

34. B 8 № 169873. Периметр ромба равен 24, а косинус одного из углов равен. Найдите площадь ромба.

35. B 8 № 169875. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.

36. B 8 № 169876. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, Делённую на .

37. B 8 № 169877. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, Делённую на .

38. B 8 № 169878. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен. Найдите площадь параллелограмма.

39. B 8 № 169879. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен. Найдите площадь параллелограмма.

40. B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен. Найдите площадь параллелограмма.

41. B 8 № 169881. Основания трапеции равны 18 и 12, одна из боковых сторон равна, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.

42. B 8 № 169882. Основания трапеции равны 18 и 10, одна из боковых сторон равна, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.

43. B 8 № 169883. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен. Найдите площадь трапеции.

44. B 8 № 169884. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен. Найдите площадь трапеции.

45. B 8 № 169885. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен. Найдите площадь трапеции.

46. B 8 № 169886. Радиус круга равен 1. Найдите его площадь, Деленную на π.

47. B 8 № 169887. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, Деленную на π.

48. B 8 № 169888. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6Π, а угол сектора равен 120°. В ответе укажите площадь, Деленную на π.

49. B 8 № 169889. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, Делённую на .

50. B 8 № 169890. В прямоугольном треугольнике один из катетов равен, острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, Делённую на .

51. B 8 № 169891. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, Делённую на .

52. B 8 № 169892. В прямоугольном треугольнике один из катетов равен, угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, Делённую на .

53. B 8 № 169893. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.

54. B 8 № 169894. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, Деленную на

55. B 8 № 169895. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, Деленную на

56. B 8 № 169896. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, Деленную на

57. B 8 № 169897. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.

58. B 8 № 169898. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны. Найдите площадь прямоугольника, Деленную на

59. B 8 № 169899. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, Деленную на

60. B 8 № 169900. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.

61. B 8 № 169901. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, Деленную на

62. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, Деленную на

63. B 8 № 169903. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, Деленную на

64. B 8 № 169904. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.

65. B 8 № 169905. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, Деленную на

66. B 8 № 169906. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.

67. B 8 № 169908. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, Деленную на

68. B 8 № 169909. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, Деленную на

69. B 8 № 169910. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.

70. B 8 № 169911. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь ромба, Деленную на

71. B 8 № 169912. Радиус круга равен 3, а длина ограничивающей его окружности равна 6Π. Найдите площадь круга. В ответ запишите площадь, Деленную на π.

72. B 8 № 169913. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6Π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, Деленную на π.

73. B 8 № 311332. В равнобедренном треугольнике. Найдите, если высота.

74. B 8 № 311375. В равнобедренном треугольнике. Найдите, если высота.

75. B 8 № 311387. В треугольнике угол равен 90°, . Найдите.

76. B 8 № 311399. В треугольнике угол равен 90°, . Найдите.

77. B 8 № 311411. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

78. B 8 № 311475. Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.

79. B 8 № 311480. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.

80. B 8 № 311498. В треугольнике угол прямой, . Найдите.

81. B 8 № 311500. В треугольнике угол прямой, . Найдите.

82. B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.

83. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.

84. B 8 № 311849. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.

85. B 8 № 311913. Найдите площадь параллелограмма, изображённого на рисунке.

86. B 8 № 311957.

Найдите площадь параллелограмма, изображённого на рисунке.

87. B 8 № 314870. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.

88. B 8 № 314876. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

89. B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

90. B 8 № 315000. Найдите площадь параллелограмма, изображённого на рисунке.

91. B 8 № 315074. Найдите площадь параллелограмма, изображённого на рисунке.

92. B 8 № 315084. Найдите площадь параллелограмма, изображённого на рисунке.

93. B 8 № 316231. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.

94. B 8 № 316258. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.

95. B 8 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.

96. B 8 № 316321. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.

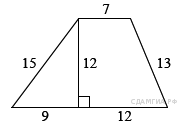
97. B 8 № 316347. Найдите площадь трапеции, изображённой на рисунке.

98. B 8 № 316373. Найдите площадь трапеции, изображённой на рисунке.

99. B 8 № 323297.

В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.

100. B 8 № 323430.

Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.

Просмотр содержимого документа
«12Figuru_na kvadratRecetke»

Фигуры на квадратной решётке

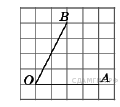
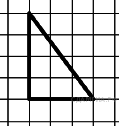
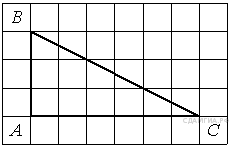
1. B 9 № 40. Найдите тангенс угла AOB, изображенного на рисунке.

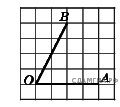
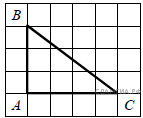
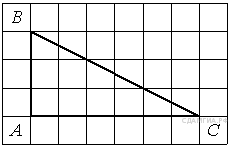
2. B 9 № 66. Найдите тангенс угла А треугольника ABC, изображённого на рисунке.

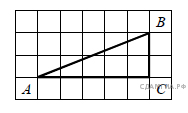
3. B 9 № 92. Найдите тангенс угла B треугольника ABC, изображённого на рисунке.

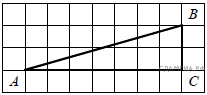
4. B 9 № 196. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.

5. B 9 № 311321. На рисунке изображена трапеция. Используя рисунок, найдите.

6. B 9 № 311333. На рисунке изображен ромб. Используя рисунок, найдите.

7. B 9 № 311344. На рисунке изображена трапеция. Используя рисунок, найдите.

8. B 9 № 311356. На рисунке изображен параллелограмм. Используя рисунок, найдите.

9. B 9 № 311366. На рисунке изображен параллелограмм. Используя рисунок, найдите.

10. B 9 № 311376. На рисунке изображен ромб. Используя рисунок, найдите.

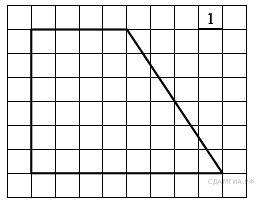
11. B 9 № 311388. На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.

12. B 9 № 311400. На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.

13. B 9 № 311485. На квадратной сетке изображён угол. Найдите.

14. B 9 № 311491. Найдите тангенс угла треугольника, изображённого на рисунке.

15. B 9 № 311495. Найдите тангенс угла треугольника, изображённого на рисунке.

16. B 9 № 311496. Найдите тангенс угла треугольника, изображённого на рисунке.

17. B 9 № 311683. Найдите тангенс угла AOB, изображенного на рисунке.

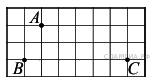
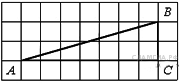
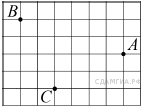
18. B 9 № 311762. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

19. B 9 № 311792. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

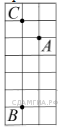
20. B 9 № 311850. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

21. B 9 № 311914.

Найдите синус острого угла трапеции, изображённой на рисунке.

22. B 9 № 311958.

На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённую из вершины прямого угла.

23. B 9 № 314836. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

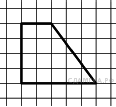
24. B 9 № 314837. Найдите площадь трапеции, изображённой на рисунке.

25. B 9 № 314996. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

26. B 9 № 315024. Найдите площадь трапеции, изображённой на рисунке.

27. B 9 № 315028. Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

28. B 9 № 315067. Найдите площадь трапеции, изображённой на рисунке.

29. B 9 № 316259. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

30. B 9 № 316285. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

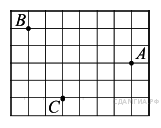
31. B 9 № 316322.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.

32. B 9 № 316348. Найдите тангенс угла, изображённого на рисунке.

33. B 9 № 316374. Найдите тангенс угла, изображённого на рисунке.

Просмотр содержимого документа
«13Geometric_Vuskazuvania»

Анализ геометрических высказываний

1. B 10 № 67. Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

2. B 10 № 93. Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

3. B 10 № 119. Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

4. B 10 № 145. Укажите номера верных утверждений.

1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

5. B 10 № 171. Укажите номера верных утверждений.

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

6. B 10 № 197. Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

7. B 10 № 169915. Какие из следующих утверждений верны?

1) Если угол равен 45°, то вертикальный с ним угол равен 45°.

2) Любые две прямые имеют ровно одну общую точку.

3) Через любые три точки проходит ровно одна прямая.

4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

8. B 10 № 169916. Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

9. B 10 № 169917. Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

10. B 10 № 169922. Какие из следующих утверждений верны?

1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

11. B 10 № 169923. Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

12. B 10 № 169924. Какие из следующих утверждений верны?

1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

13. B 10 № 169926. Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.

4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

14. B 10 № 169928. Какие из следующих утверждений верны?

1) Около всякого треугольника можно описать не более одной окружности.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

15. B 10 № 169929. Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

16. B 10 № 169930. Какие из следующих утверждений верны?

1) Окружность имеет бесконечно много центров симметрии.

2) Прямая не имеет осей симметрии.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Квадрат не имеет центра симметрии.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

17. B 10 № 169931. Какие из следующих утверждений верны?

1) Правильный шестиугольник имеет шесть осей симметрии.

2) Прямая не имеет осей симметрии.

3) Центром симметрии ромба является точка пересечения его диагоналей.

4) Равнобедренный треугольник имеет три оси симметрии.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

18. B 10 № 169932. Какие из следующих утверждений верны?

1) Центром симметрии прямоугольника является точка пересечения диагоналей.

2) Центром симметрии ромба является точка пересечения его диагоналей.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

19. B 10 № 169933. Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

20. B 10 № 169934. Какие из следующих утверждений верны?

1) Любые два прямоугольных треугольника подобны.

2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

3) Стороны треугольника пропорциональны косинусам противолежащих углов.

4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

21. B 10 № 169935. Какие из следующих утверждений верны?

1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

22. B 10 № 169936. Какие из следующих утверждений верны?

1) Если площади фигур равны, то равны и сами фигуры.

2) Площадь трапеции равна произведению суммы оснований на высоту.

3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.

4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

23. B 10 № 169938. Какие из следующих утверждений верны?

1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.

2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.

3) Площадь трапеции меньше произведения суммы оснований на высоту.

4) Площадь прямоугольного треугольника меньше произведения его катетов.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

24. B 10 № 311406. На рисунке изображён график функции. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

4) прямая пересекает график в точках и

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

25. B 10 № 311684. Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

26. B 10 № 311763. Укажите номера верных утверждений.

1) Через любую точку проходит не менее одной прямой.

2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

27. B 10 № 311851. Укажите номера верных утверждений.

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.

2) Через любые три точки проходит не более одной прямой.

3) Сумма вертикальных углов равна 180°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

28. B 10 № 311915. Укажите номера верных утверждений.

1) Площадь трапеции равна половине высоты, умноженной на разность оснований.

2) Через любые две точки можно провести прямую.

3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

29. B 10 № 311959. Укажите номера верных утверждений.

1) В любую равнобедренную трапецию можно вписать окружность.

2) Диагональ параллелограмма делит его углы пополам.

3) Площадь прямоугольного треугольника равна половине произведения его катетов.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

30. B 10 № 314814. Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

31. B 10 № 314818. Какие из данных утверждений верны? Запишите их номера.

1) Каждая из биссектрис равнобедренного треугольника является его медианой.

2) Диагонали прямоугольника равны.

3) У любой трапеции боковые стороны равны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

32. B 10 № 314894. Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.

2) Диагональ трапеции делит её на два равных треугольника.

3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

33. B 10 № 316233. Укажите номера верных утверждений.

1) Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

34. B 10 № 316286. Укажите номера верных утверждений.

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

35. B 10 № 316323. Укажите номера верных утверждений.

1) Любые три прямые имеют не более одной общей точки.

2) Если угол равен 120°, то смежный с ним равен 120°.

3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

36. B 10 № 316349. Укажите номера неверных утверждений.

1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

2) Диагонали ромба перпендикулярны.

3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

37. B 10 № 333015. Какие из следующих утверждений верны?

1) Через точку, не лежащую на данной прямой, можно провести прямую,

Параллельную этой прямой.

2) Если диагонали параллелограмма равны, то это ромб.

3) Для точки, лежащей на окружности, расстояние до центра окружности

38. B 10 № 333094. Какие из следующих утверждений верны?

1) Любой прямоугольник можно вписать в окружность.

2) Все углы ромба равны.

3) Треугольник со сторонами 1, 2, 4 существует.

39. B 10 № 333120. Какие из следующих утверждений верны?

1) Площадь треугольника меньше произведения двух его сторон.

2) Средняя линия трапеции равна сумме её оснований.

3) Если два угла одного треугольника равны двум углам другого треуголь-

Ника, то такие треугольники подобны.

40. B 10 № 333147. Какие из следующих утверждений верны?

1) Средняя линия трапеции равна сумме её оснований.

2) Диагонали ромба перпендикулярны.

3) Площадь треугольника меньше произведения двух его сторон.

Просмотр содержимого документа
«14Analiz_DiagramTablisGrafikov (1)»

Анализ диаграмм, таблиц, графиков

1. A 4 № 30. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?

1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.

2. A 4 № 56. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.

1) 026A
2) 002A
3) 038A
4) 016A

3. A 4 № 82. Студентка Цветкова выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

Отправление

На Киевский вокзал

Путь от вокзала до университета занимает 45 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студентке.

4. A 4 № 108. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Дети от 1 года до 14 лет

Какой вывод о суточном потреблении жиров 10-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 102 г жиров?

1) Потребление в норме.
2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы.
4) В таблице недостаточно данных.

5. A 4 № 134. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Дети от 1 года до 14 лет

Какой вывод о суточном потреблении углеводов 12-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 359 г углеводов?

6. A 4 № 160. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Дети от 1 года до 14 лет

Какой вывод о суточном потреблении жиров 8-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров?

7. A 4 № 311290. Дорожный знак, изображённый на рисунке, называется «Ограничение высоты». Его устанавливают перед мостами, тоннелями и прочими сооружениями, чтобы запретить проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную высоту.

Какому из данных транспортных средств этот знак запрещает проезд?

1) молоковозу высотой 3770 мм
2) пожарному автомобилю высотой 3400 мм
3) автотопливозаправщику высотой 2900 мм
4) автоцистерне высотой 3350 мм

8. A 4 № 311291. Дорожный знак, изображённый на рисунке, называется «Ограничение длины». Его устанавливают там, где запрещён проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную длину.

Какому из данных транспортных средств этот знак запрещает проезд?

1) бензовозу длиной 7600 мм
2) автомобилю Газель длиной 6330 мм
3) автотопливозаправщику длиной 10 200 мм
4) автоцистерне длиной 8250 мм

9. A 4 № 311292. Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 65,8 г.

Масса одного яйца, г

1) Высшая
2) Отборная
3) Первая
4) Вторая

10. A 4 № 311293. В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.

Время (мин. и сек.)

Какую отметку получит девочка, пробежавшая на лыжах 1 км за 6 минут 15 секунд?

11. A 4 № 311294. Бабушка, живущая в Краснодаре, отправила 1 сентября четыре посылки своим внукам, живущим в разных городах России. В таблице дано контрольное время в сутках, установленное для пересылки посылок наземным транспортом (без учёта дня приёма) между некоторыми городами России.

Пункт отправки

Пункт назначения

Архангельск

Какая из данных посылок не была доставлена вовремя?

1) пункт назначения — Белгород, посылка доставлена 10 сентября
2) пункт назначения — Астрахань, посылка доставлена 12 сентября
3) пункт назначения — Барнаул, посылка доставлена 15 сентября
4) пункт назначения — Архангельск, посылка доставлена 11 сентября

12. A 4 № 311295. Для квартиры площадью 50 м 2 заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.

Цвет потолка

Цена (в руб.) за 1 м (в зависимости от площади помещения)

До 10 м

От 11 до 30 м

От 31 до 60 м

Свыше 60 м

Какова стоимость заказа, если действует сезонная скидка в 10%?

1) 35 000 руб.
2) 3 500 руб.
3) 34 990 руб.
4) 31 500 руб.

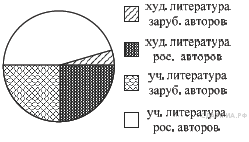
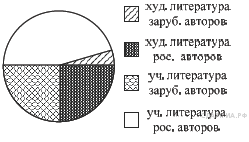
13. A 4 № 311296. Фонд школьной библиотеки, состоящей из учебной и художественной литературы российских и зарубежных авторов, представлен в виде диаграммы. Сколько примерно книг учебной литературы в библиотеке, если всего в библиотечном фонде 800 книг?

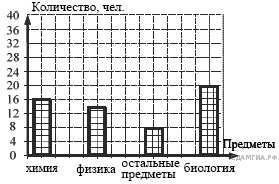
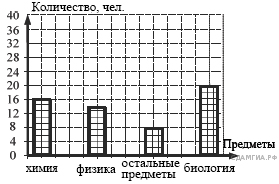
14. A 4 № 311297. Завуч школы подвел итоги по выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты представлены на диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ физику?

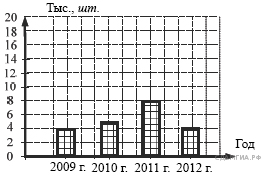
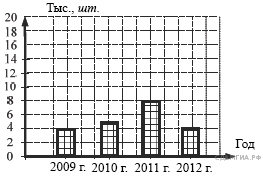
15. A 4 № 311298. На диаграмме показано количество посаженных деревьев и кустарников в г. Сочи за период с 2009 по 2012 гг. Определите, сколько всего было посажено зелёных насаждений за 2011 г. и 2012 г.?

1) 10 000
2) 4 000
3) 12 000
4) 8 000

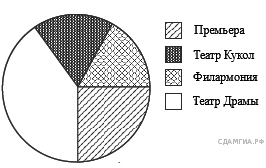
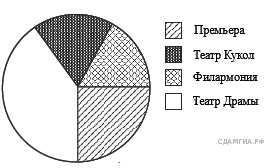
16. A 4 № 311299. На диаграмме показано количество школьников, посетивших театры г. Краснодара за 2010 г. Определите, сколько примерно зрителей посетили за этот период Филармонию, если во всех этих театрах школьников было 2000 человек.

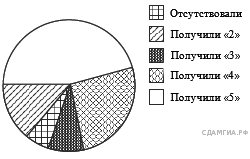
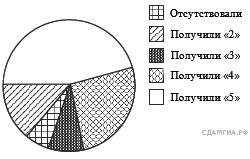
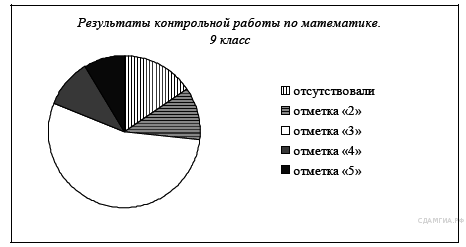
17. A 4 № 311300. Учитель математики подвел итоги контрольной работы по алгебре среди учащихся 9-х классов. Результаты представлены на диаграмме. Сколько примерно учащихся получили отметку «4» и «5», если всего в этих классах учатся 200 учащихся?

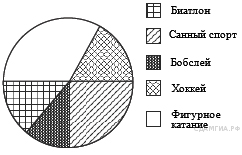
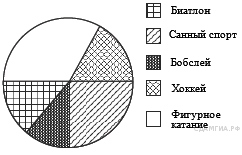
18. A 4 № 311301. Учащимся сочинских школ был задан вопрос: «По какому виду спорта вы хотели бы посетить соревнования на Зимней олимпиаде в Сочи?». Их ответы можно увидеть на диаграмме. Сколько примерно учащихся хотели бы посетить соревнования и по хоккею, и по санному спорту, если всего в опросе приняли участие 400 школьников?

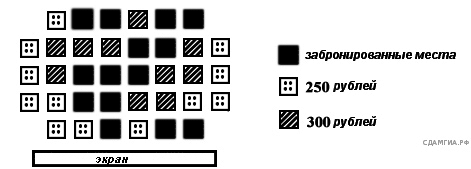
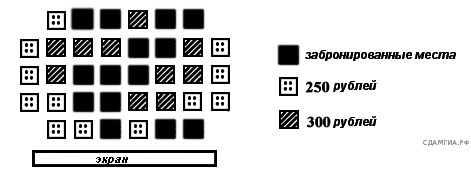
19. A 4 № 311423. На схеме зала кинотеатра отмечены разной штриховкой места с различной стоимостью билетов, а черным закрашены забронированные места на некоторый сеанс.

Сколько рублей заплатят за 5 билетов на этот сеанс пятеро друзей, если они хотят сидеть на одном ряду и выбирают самый дешевый вариант?

1) 1300
2) 1250
3) 1350
4) 1500

20. A 4 № 311425. В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах:

Орехи (за кг.)

Шоколад (за плитку)

Зефир (за кг.)

Лариса Кузьминична хочет купить 0,4 кг орехов, 5 плиток шоколада и 1,5 кг зефира. В каком магазине стоимость такой покупки будет наименьшей, если в «Камее» проходит акция: скидка 20% на орехи и зефир, а в «Машеньке» скидка 10% на все продукты?

1) В «Машеньке»
2) В «Лидии»
3) В «Камее»
4) Во всех магазинах стоимость покупки будет одинаковой

21. A 4 № 311427. В таблице представлены нормативы по технике чтения в 3 классе.

Количество прочитанных слов минуту

Первое полугодие

Второе полугодие

Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?

22. A 4 № 311429. Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Петрову.

1) 038А
2) 020У
3) 016А
4) 116С

23. A 4 № 311432. Учёный Комаров выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Комарову.

1) 032AB
2) 026A
3) 002A
4) 004A

24. A 4 № 311434. Студент Петров выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

Отправление от ст. Нара

Прибытие на Киевский вокзал

Путь от вокзала до университета занимает 40 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студенту.

25. A 4 № 311436. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Дети от 1 года до 14 лет

Какой вывод о суточном потреблении жиров женщиной можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 55 г. жиров?

26. A 4 № 311437. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Дети от 1 года до 14 лет

Какой вывод о суточном потреблении углеводов мужчиной можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 488 г. углеводов?

27. A 4 № 311675. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?

1) Отметка«5».
2) Отметка«4».
3) Отметка«3».
4) Норматив не выполнен.

28. A 4 № 311752. В таблице представлены нормативы по технике чтения в третьем классе.

Количество прочитанных слов в минуту

I и II четверти

III и IV четверти

Какую отметку получит третьеклассник, прочитавший в феврале 65 слов за минуту?

29. A 4 № 311901. В таблице приведены нормативы по прыжкам в длину с места для 11 класса.

Какую отметку получит мальчик, прыгнувший на 215 см?

30. A 4 № 311945. В таблице даны результаты олимпиад по истории и обществознанию в 10 «А» классе.

Балл по истории

Балл по обществознанию

Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 130 или хотя бы по одному предмету набрано не меньше 70 баллов. Сколько человек из 10 «А», набравших меньше 60 баллов по истории, получат похвальные грамоты?

31. A 4 № 314133. Студент Петров выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

32. A 4 № 314134. Бизнесмен Соловьёв выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Соловьёву.

1) 038А
2) 020У
3) 016А
4) 030А

33. A 4 № 314135. Учёный Комаров выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30.

В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

1) 032АВ
2) 026А
3) 002А
4) 004А

34. A 4 № 314136. Студент Сидоров выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:30. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

Отправление от ст. Нара

Путь от вокзала до университета занимает 35 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студенту.

35. A 4 № 314147. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

1) 026А
2) 002А
3) 038А
4) 016А

36. A 4 № 314199. Студентка Цветкова выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве

37. A 4 № 314202. Студентка Фиалкова выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 8:30. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

Путь от вокзала до университета занимает 40 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студентке.

38. A 4 № 314206. Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

1) 038А
2) 020У
3) 016А
4) 116С

39. A 4 № 316223. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.

Превышение скорости, км/ч

Размер штрафа, руб.

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

40. A 4 № 316250. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.

Превышение скорости, км/ч

Размер штрафа, руб.

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 112 км/ч на участке дороги с максимальной разрешённой скоростью 90 км/ч?

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

41. A 4 № 316276. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.

Превышение скорости, км/ч

Размер штрафа, руб.

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 103 км/ч на участке дороги с максимальной разрешённой скоростью 60 км/ч?

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

42. A 4 № 316313. В таблице представлены нормативы по технике чтения в третьем классе.

Количество прочитанных слов в минуту

I и II четверти

III и IV четверти

Какую отметку получит третьеклассник, прочитавший в ноябре 82 слова за минуту?

43. A 4 № 316339. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля (в л. с.*)

Налоговая ставка (в руб. за л. с. в год)

*л. с. − лошадиная сила

Сколько рублей должен заплатить владелец автомобиля мощностью 162 л. с. в качестве налога за один год?

44. A 4 № 316365. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля (в л. с.*)

Налоговая ставка (в руб. за л. с. в год)

*л. с. − лошадиная сила

Сколько рублей должен заплатить владелец автомобиля мощностью 185 л. с. в качестве налога за один год?

45. A 4 № 333084. Для квартиры площадью 135 м 2 заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.

Цвет потолка

Цена в рублях за 1 м 2 (в зависмости от площали помещения)

От 11 до 30 м 2

От 31 до 60 м 2

Какова стоимость заказа, если действует сезонная скидка в 20%?

1) 81 000 рублей
2) 64 800 рублей
3) 6480 рублей
4) 80 980 рублей

46. A 4 № 333110. В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,5 с.

Укажите номера дорожек, по которым бежали мальчики, получившие зачет.

1) I, IV
2) II, III
3) только III
4) только IV

47. A 4 № 333137. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года.

Размер штрафа, руб

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 105 км/ч на участке дороги с максимальной разрешённой скоростью 50 км/ч?

1) 500 рублей
2) 1000 рублей
3) 2000 рублей
4) 5000 рублей

Просмотр содержимого документа
«14Analiz_DiagramTablisGrafikov»

Анализ диаграмм, таблиц, графиков

1. A 4 № 30. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?

1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

1) 026A
2) 002A
3) 038A
4) 016A

Отправление

На Киевский вокзал

Дети от 1 года до 14 лет

Дети от 1 года до 14 лет

Какому из данных транспортных средств этот знак запрещает проезд?

Масса одного яйца, г

1) Высшая
2) Отборная
3) Первая
4) Вторая

10. A 4 № 311293. В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.

Время (мин. и сек.)

Какую отметку получит девочка, пробежавшая на лыжах 1 км за 6 минут 15 секунд?

Пункт отправки

Пункт назначения

Архангельск

Какая из данных посылок не была доставлена вовремя?

Цвет потолка

Цена (в руб.) за 1 м (в зависимости от площади помещения)

До 10 м

От 11 до 30 м

От 31 до 60 м

Свыше 60 м

Какова стоимость заказа, если действует сезонная скидка в 10%?

1) 35 000 руб.
2) 3 500 руб.
3) 34 990 руб.
4) 31 500 руб.

1) 10 000
2) 4 000
3) 12 000
4) 8 000

1) 1300
2) 1250
3) 1350
4) 1500

20. A 4 № 311425. В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах:

Орехи (за кг.)

Шоколад (за плитку)

Зефир (за кг.)

1) В «Машеньке»
2) В «Лидии»
3) В «Камее»
4) Во всех магазинах стоимость покупки будет одинаковой

21. A 4 № 311427. В таблице представлены нормативы по технике чтения в 3 классе.

Количество прочитанных слов минуту

Первое полугодие

Второе полугодие

Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

1) 038А
2) 020У
3) 016А
4) 116С

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

1) 032AB
2) 026A
3) 002A
4) 004A

Отправление от ст. Нара

Прибытие на Киевский вокзал

Дети от 1 года до 14 лет

27. A 4 № 311675. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?

1) Отметка«5».
2) Отметка«4».
3) Отметка«3».
4) Норматив не выполнен.

28. A 4 № 311752. В таблице представлены нормативы по технике чтения в третьем классе.

Количество прочитанных слов в минуту

I и II четверти

III и IV четверти

Какую отметку получит третьеклассник, прочитавший в феврале 65 слов за минуту?

29. A 4 № 311901. В таблице приведены нормативы по прыжкам в длину с места для 11 класса.

Какую отметку получит мальчик, прыгнувший на 215 см?

30. A 4 № 311945. В таблице даны результаты олимпиад по истории и обществознанию в 10 «А» классе.

Балл по истории

Балл по обществознанию

1) 038А
2) 020У
3) 016А
4) 030А

В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

1) 032АВ
2) 026А
3) 002А
4) 004А

Отправление от ст. Нара

1) 026А
2) 002А
3) 038А
4) 016А

1) 038А
2) 020У
3) 016А
4) 116С

Превышение скорости, км/ч

Размер штрафа, руб.

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

Превышение скорости, км/ч

Размер штрафа, руб.

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

Превышение скорости, км/ч

Размер штрафа, руб.

1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей

42. A 4 № 316313. В таблице представлены нормативы по технике чтения в третьем классе.

Количество прочитанных слов в минуту

I и II четверти

III и IV четверти

Какую отметку получит третьеклассник, прочитавший в ноябре 82 слова за минуту?

43. A 4 № 316339. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля (в л. с.*)

Налоговая ставка (в руб. за л. с. в год)

*л. с. − лошадиная сила

Сколько рублей должен заплатить владелец автомобиля мощностью 162 л. с. в качестве налога за один год?

44. A 4 № 316365. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля (в л. с.*)

Налоговая ставка (в руб. за л. с. в год)

*л. с. − лошадиная сила

Сколько рублей должен заплатить владелец автомобиля мощностью 185 л. с. в качестве налога за один год?

Цвет потолка

Цена в рублях за 1 м 2 (в зависмости от площали помещения)

От 11 до 30 м 2

От 31 до 60 м 2

Какова стоимость заказа, если действует сезонная скидка в 20%?

1) 81 000 рублей
2) 64 800 рублей
3) 6480 рублей
4) 80 980 рублей

Укажите номера дорожек, по которым бежали мальчики, получившие зачет.

1) I, IV
2) II, III
3) только III
4) только IV

Размер штрафа, руб

1) 500 рублей
2) 1000 рублей
3) 2000 рублей
4) 5000 рублей

Просмотр содержимого документа
«16Prost_Tekst_Zadaci»

Простейшие текстовые задачи

1. B 12 № 43. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?

2. B 12 № 69. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?

3. B 12 № 95. Альбом, который стоил 120 рублей, продаётся с 25%-ой скидкой. При покупке 5 таких альбомов покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?

4. B 12 № 121. Чайник, который стоил 800 рублей, продаётся с 5%-ой скидкой. При покупке этого чайника покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?

5. B 12 № 147. Набор полотенец, который стоил 200 рублей, продаётся с 3%-й скидкой. При покупке этого набора покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?

6. B 12 № 173. Пылесос, который стоил 3500 рублей, продаётся с 10%-й скидкой. При покупке этого пылесоса покупатель отдал кассиру 5000 рублей. Сколько рублей сдачи он должен получить?

7. B 12 № 199. Блюдце, которое стоило 40 рублей, продаётся с 10%-й скидкой. При покупке 10 таких блюдец покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?

8. B 12 № 137243. Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?

9. B 12 № 137244. Перед представлением в цирк для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано всех воздушных шариков, а в антракте – еще 12 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?

10. B 12 № 137245. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?

11. B 12 № 137246. Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?

12. B 12 № 137247. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?

13. B 12 № 137248. Акции предприятия распределены между государством и частными лицами в отношении 3:5. Общая прибыль предприятия после уплаты налогов за год составила 32 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?

Ответ укажите в рублях.

14. B 12 № 137249. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?

15. B 12 № 137250. Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?

16. B 12 № 137251. Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120% среднего веса. Сколько весит Сергей?

17. B 12 № 137252. В начале года число абонентов телефонной компании «Север» составляло 200 тыс. чел., а в конце года их стало 210 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?

18. B 12 № 137253. Тест по математике содержит 30 заданий, из которых 18 заданий по алгебре, остальные –– по геометрии. В каком отношении содержатся в тесте алгебраические и геометрические задания?

Варианты ответа

19. B 12 № 137254. Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?

20. B 12 № 137257. На счет в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет?

21. B 12 № 137258. Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой?

22. B 12 № 137259. Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько рублей стоил товар до распродажи?

23. B 12 № 137262. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?

24. B 12 № 137263. Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?

25. B 12 № 137264. В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20% от предыдущей цены. Сколько рублей будет стоить товар на двенадцатый день после поступления в продажу?

26. B 12 № 137265. Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120% среднего веса. Сколько килограммов весит Сергей?

27. B 12 № 311687. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?

28. B 12 № 311765. Поступивший в продажу в январе мобильный телефон стоил 3000 рублей. В марте он стал стоить 2790 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по март?

29. B 12 № 311795. Поступивший в продажу в январе мобильный телефон стоил 3000 рублей. В апреле он стал стоить 2160 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по апрель?

30. B 12 № 311821. Клубника стоит 180 рублей за килограмм, а клюква — 250 рублей за килограмм. На сколько процентов клубника дешевле клюквы?

31. B 12 № 311853. Виноград стоит 160 рублей за килограмм, а малина — 200 рублей за килограмм. На сколько процентов виноград дешевле малины?

32. B 12 № 311917. На многопредметной олимпиаде всех участников получили дипломы, остальных участников были награждены похвальными грамотами, а остальные 144 человека получили сертификаты об участии. Сколько человек участвовало в олимпиаде?

33. B 12 № 311961. На складе есть коробки с ручками двух цветов: чёрные и синие. Коробок с чёрными ручками 4, с синими — 11. Сколько всего ручек на складе, если чёрных ручек 640, коробки одинаковые и в каждой коробке находятся ручки только одного цвета?

34. B 12 № 314120. Кисть, которая стоила 240 рублей, продаётся с 25%-й скидкой. При покупке двух таких кистей покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?

35. B 12 № 314122. Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?

36. B 12 № 314125. Спортивный магазин проводит акцию: «Любая футболка по цене 300 рублей. При покупке двух футболок — скидка на вторую 60%». Сколько рублей придётся заплатить за покупку двух футболок?

37. B 12 № 314405. В течение августа помидоры подешевели на 50%, а затем в течение сентября подорожали на 70%. Какая цена меньше: в начале августа или в конце сентября — и на сколько процентов?

38. B 12 № 316235. Клубника стоит 180 рублей за килограмм, а клюква — 250 рублей за килограмм. На сколько процентов клубника дешевле клюквы?

39. B 12 № 316262. Виноград стоит 160 рублей за килограмм, а малина — 200 рублей за килограмм. На сколько процентов виноград дешевле малины?

40. B 12 № 316288. Черешня стоит 150 рублей за килограмм, а виноград — 160 рублей за килограмм. На сколько процентов черешня дешевле винограда?

41. B 12 № 316325. Поступивший в продажу в апреле мобильный телефон стоил 4000 рублей. В сентябре он стал стоить 2560 рублей. На сколько процентов снизилась цена на мобильный телефон в период с апреля по сентябрь?

42. B 12 № 316351. На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?

43. B 12 № 316377. На молочном заводе пакеты молока упаковываются по 15 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока вдвое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 32?

Просмотр содержимого документа
«17Praktic_ZadaciPOGeometrii»

Практические задачи по геометрии

1. B 13 № 44. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

2. B 13 № 70. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

3. B 13 № 96. От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.

4. B 13 № 148. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

5. B 13 № 200. От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.

6. B 13 № 132751. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?

7. B 13 № 132752. Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?

8. B 13 № 132753. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут?

9. B 13 № 132754. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?

10. B 13 № 132755. В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой — 6 м. Найдите расстояние (в метрах) между их верхушками.

11. B 13 № 132756. Колесо имеет 18 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.

12. B 13 № 132757. Сколько спиц в колесе, если угол между соседними спицами равен 18°?

13. B 13 № 132758. Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?

14. B 13 № 132759. Какой угол (в градусах) описывает минутная стрелка за 10 мин?

15. B 13 № 132760. Какой угол (в градусах) описывает часовая стрелка за 20 мин?

16. B 13 № 132761. На какой угол (в градусах) поворачивается минутная стрелка пока часовая проходит?

17. B 13 № 132764. Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

18. B 13 № 132765. Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.

19. B 13 № 132766. Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.

20. B 13 № 132767. Найдите периметр прямоугольного участка земли, площадь которого равна 800 м 2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.

21. B 13 № 132772. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?

22. B 13 № 311323. Определите, сколько необходимо закупить пленки для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.

23. B 13 № 311335. На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите длину пути (в м), если масштаб 1 см : 10 000 см.

24. B 13 № 311346. Определите, сколько необходимо закупить пленки для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.

25. B 13 № 311358. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см 2 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).

26. B 13 № 311368. Дизайнер Алина получила заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см 2 ) необходимо закупить Алине, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань она будет обклеивать отдельно (без загибов).

27. B 13 № 311378. На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см: 10000 см.

28. B 13 № 311390. Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 4 часа?

29. B 13 № 311402. Колесо имеет 5 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.

30. B 13 № 311414. Сколько всего осей симметрии имеет фигура, изображённая на рисунке?

31. B 13 № 311502. Склоны горы образуют с горизонтом угол, косинус которого равен 0,8. Расстояние по карте между точками A и B равно 10 км. Определите длину пути между этими точками через вершину горы.

32. B 13 № 311506. Склоны горы образуют с горизонтом угол, косинус которого равен 0,9. Расстояние по карте между точками A и B равно 18 км. Определите длину пути между этими точками через вершину горы.

33. B 13 № 311509. Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.

34. B 13 № 311513. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?

35. B 13 № 311516. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 4 м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5 м?

36. B 13 № 311519. Определите высоту дома, ширина фасада которого равна 8 м, высота от фундамента до крыши равна 4 м, а длина ската крыши равна 5 м.

37. B 13 № 311522. Определите высоту дома, ширина фасада которого равна 6 м, высота от фундамента до крыши равна 4 м, а длина ската крыши равна 5 м.

38. B 13 № 311524. Лестница соединяет точки и, расстояние между которыми равно 25 м. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите высоту (в метрах), на которую поднимается лестница.

39. B 13 № 311526. Обхват ствола секвойи равен 4,8 м. Чему равен его диаметр (в метрах)? Ответ округлите до десятых.

40. B 13 № 311527. Обхват ствола секвойи равен 6,3 м. Чему равен его диаметр (в метрах)? Ответ округлите до целого.

41. B 13 № 311688. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

42. B 13 № 311766. Мальчик прошёл от дома по направлению на восток 550 м. Затем повернул на север и прошёл 480 м. На каком расстоянии (в метрах) от дома оказался мальчик?

43. B 13 № 311854. Девочка прошла от дома по направлению на запад 20 м. Затем повернула на север и прошла 800 м. После этого она повернула на восток и прошла ещё 200 м. На каком расстоянии (в метрах) от дома оказалась девочка?

44. B 13 № 311918. Глубина бассейна составляет 2 метра, ширина — 10 метров, а длина — 25 метров. Найдите суммарную площадь боковых стен и дна бассейна (в квадратных метрах).

45. B 13 № 311962. Лестница соединяет точки A и B и состоит из 35 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).

46. B 13 № 314808. Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

47. B 13 № 314820. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

48. B 13 № 314833. От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.

49. B 13 № 314835. Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

50. B 13 № 314845. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.

51. B 13 № 314889. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?

52. B 13 № 314914. Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

53. B 13 № 314981. Сторона ромба равна 28, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

54. B 13 № 315016. Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?

55. B 13 № 315080. В треугольнике ABC угол C прямой, AC = 4 , CosA = 0,8 . Найдите AB.

56. B 13 № 315106. От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.

57. B 13 № 316236. Девочка прошла от дома по направлению на запад 340 м. Затем повернула на север и прошла 60 м. После этого она повернула на восток и прошла ещё 420 м. На каком расстоянии (в метрах) от дома оказалась девочка?

58. B 13 № 316263. Девочка прошла от дома по направлению на запад 20 м. Затем повернула на север и прошла 800 м. После этого она повернула на восток и прошла ещё 200 м. На каком расстоянии (в метрах) от дома оказалась девочка?

59. B 13 № 316289. Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?

60. B 13 № 316326. Мальчик прошёл от дома по направлению на восток 400 м. Затем повернул на север и прошёл 90 м. На каком расстоянии (в метрах) от дома оказался мальчик?

61. B 13 № 316352. Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.

62. B 13 № 316378. Длина стремянки в сложенном виде равна 1,11 м, а расстояние между её основаниями в разложенном виде составляет 0,72 м. Найдите высоту (в метрах) стремянки в разложенном виде.

Просмотр содержимого документа
«18Analiz_Diagram»

Анализ диаграмм

1. B 14 № 31. Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.

Какое из утверждений относительно результатов контрольной работы Неверно, если всего в школе 120 девятиклассников?

1) Более половины учащихся получили отметку «3».

2) Около четверти учащихся отсутствовали на контрольной работе или получили отметку «2».

3) Отметку «4» или «5» получила примерно шестая часть учащихся.

4) Отметку «3», «4» или «5» получили более 100 учащихся.

В ответ запишите номер выбранного утверждения.

2. B 14 № 57. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей. Какое из следующих утверждений Неверно?

1) Пользователей из России больше, чем пользователей с Украины.

2) Пользователей из Белоруссии больше, чем пользователей из Швеции.

3) Больше трети пользователей сети — из Украины.

4) Пользователей из России больше 4 миллионов.

В ответ запишите номер этого утверждения.

3. B 14 № 83. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. Какое из следующих утверждений Неверно?

1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.

2) Пользователей из Украины больше, чем пользователей Латвии.

3) Примерно две трети общего числа пользователей — из России.

4) Пользователей из Украины больше 3 миллионов.

В ответ запишите номер выбранного утверждения.

4. B 14 № 109. На диаграмме представлены семь крупнейших по площади территории (в млн км 2 ) стран мира. Какое из следующих утверждений Неверно?

1) Площадь территории Индии составляет

2) Площадь Китая больше площади Австралии.

3) Россия — крупнейшая по площади территории страна мира.

4) площадь Канады больше площади США на

В ответ запишите номер выбранного утверждения.

5. B 14 № 135. На диаграмме представлены семь крупнейших по площади территории (в млн км 2 ) стран мира. Какое из следующих утверждений Верно?

1) Площадь Австралии больше площади Китая.

2)Площадь России больше площади Бразилии более чем вдвое.

3) Площадь территории Индии составляет 4 млн км 2

4) Аргентина входит в семерку крупнейших по площади территории стран мира.

В ответе запишите номер выбранного утверждения.

6. B 14 № 161. На диаграмме представлены семь крупнейших по площади территории (в млн км 2 ) стран мира. Какое из следующих утверждений Верно?

1) Площадь России больше площади США на 10 млн км 2 .

2) Площадь Индии больше площади Австралии.

3) Афганистан входит в семёрку крупнейших по площади территории стран мира.

4) Площадь территории Бразилии составляет 8,5 млн км 2 .

В ответе запишите номер выбранного утверждения.

7. B 14 № 187. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей. Какое из следующих утверждений Неверно?

1) Пользователей из Беларуси меньше, чем пользователей из Украины.

2) Пользователей из России больше 4 миллионов.

3) Пользователей из Украины больше четверти общего числа пользователей.

4) Пользователей из Беларуси больше, чем пользователей из Финляндии.

В ответе запишите номер выбранного утверждения.

8. B 14 № 206046. На диаграмме показано содержание питательных веществ в сливочном мороженом. Определите по диаграмме, содержание каких веществ преобладает.

*-к прочему относятся вода, витамины и минеральные вещества.

11. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь, Делённую на

Просмотр содержимого документа «14Analiz_DiagramTablisGrafikov (1)»

После этого она по вер ну ла на во сток и про шла еще 100 м.

Multiurok. ru

02.09.2020 11:41:00

2020-01-10 13:06:44

Источники:

Https://multiurok. ru/files/material-po-matematike-dlia-podgotovki-k-oge. html

Источник

Сложность:

Задание 17 номер 169850

Среднее время решения: 3 мин. 23 сек.

ЕГЭ по математике 2022 задание 8: номер 170 | Ювелирное изделие состоит из …
35

Ювелирное изделие состоит из серебра и золота. В начале года серебро дорожает на $5%$, а золото — на $20%$ по сравнению с предыдущим годом, в результате чего стоимость ювелирного изделия увеличивается на $15%$. Какую часть ювелирного изделия составляет золото, если в предыдущем году $1$ г золота стоил в $18$ раз дороже $1$ г серебра? (Ответ дать в виде десятичной дроби.)

Объект авторского права ООО «Легион»

Вместе с этой задачей также решают:

Свежие подосиновики содержат $78%$ воды, а сушёные — $12%$. Сколько килограммов свежих подосиновиков требуется для получения $3$ кг сушёных грибов?

Имеется два раствора. Первый содержит $10%$ соли, второй — $20%$ соли. Из этих двух растворов получили третий раствор массой $ 50$ кг, содержащий $12%$ соли. На сколько килограммов масса в…

Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо здания вокзала, длина которого равна 150 метров, за 1 минуту. Найдите длину поезда в метрах.

От замка А к замку В, расстояние между которыми $20$ км, одновременно вылетели два почтовых голубя. Известно, что за час первый голубь пролетает на $20$ км меньше, чем второй. Найдите …

People in contemporary world can hardly imagine their lives without machines. Every day either a new gadget is invented or an old one is improved. Different people appreciate new inventions differently. Some suppose that sophisticated gadgets are really useful and necessary, while others find them absolutely awful as they influence people badly. As for me, I am pretty sure that gadgets make people`s lives easier.

Firstly, they do all kinds of dirty and hard work, as cleaning. Secondly, devices can save a lot of time as well as storage space. For instance, a computer disk can contain the same amount of information as several thick books.So, machines help people in different spheres.

However, opponents of this point of view are definitely sure that gadgets affect people negatively. People are reluctant to work due to the influence of machines. People become lazy and disorganized. They just expect their latest gadgets to do everything instead of them. Moreover, according to scientists, a great number of widespread devices produce radiation that can cause serious health problems. Furthermore, more and more people are becoming addicted to their modern gadgets, for instance computers, TVs or mobile phones. So, they neglect their home obligations, work or school and spend all their spare time in front of a laptop screen or a TV-set.

In conclusion, I firmly believe that in spite of all drawbacks, gadgets have, their benefits are much more considerable, as they save people`s time and let them enjoy life.

Перевод:

Современный человек едва ли может представить свою жизнь без машин. Ежедневно или появляются новые устройства, или улучшаются уже существующие. Люди по-разному относятся к новым изобретениям. Некоторые полагают, что сложные гаджеты на самом деле полезны и необходимо, в то время, как другие считают их ужасными из-за их отрицательного влияния на людей. Что касается меня, я абсолютно уверена в том, что новые устройства делают нашу жизнь легче.

Во-первых, они выполняют всю грязную и тяжелую работу, такую как уборка. Во-вторых, устройства экономят как время, так и место. Например, компьютерный диск может вмещать столько же информации, как несколько толстых книг. Итак, машины помогают людям в разных сферах деятельности.

Однако противники этой точки зрения абсолютно уверены в том, что новые изобретения отрицательно влияют на людей. Люди не хотят работать из-за влияния устройств. Они становятся ленивыми и неорганизованными. Они ждут, когда их последние изобретения сделают всё за них. Более того, по мнению ученых, многие широко распространенные гаджеты обладают излучением, которое может вызвать серьёзные проблемы со здоровьем. Кроме того, всё больше и больше людей становятся зависимыми от компьютера, телевизора или мобильного телефона. Они игнорируют свои домашние обязанности, учебу или работу и проводят всё своё время перед ноутбуком или экраном телевизора.

В заключение, я считаю, что, несмотря на все имеющиеся недостатки, достоинства гаджетов намного более занчительны, так как они экономят время и позволяют людям наслаждаться жизнью!

Источник

Задание № 17, ОГЭ, математика

Окружность. Круг. Часы. Земля. Колесо.

Раздел 1.

Найдите угол, который минутная стрелка описывает за 15 минут. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 25 минут. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 16 минут. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 4 минуты. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 23 минуты. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 12 минут. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 28 минут. Ответ дайте в градусах.

Найдите угол, который минутная стрелка описывает за 7 минут. Ответ дайте в градусах.

Раздел 2.

Какой угол (в градусах) описывает часовая стрелка за 2 часа 4 минуты?

Какой угол (в градусах) описывает часовая стрелка за 1 час 44 минуты?

Какой угол (в градусах) описывает часовая стрелка за 10 минут?

Какой угол (в градусах) описывает часовая стрелка за 4 часа 10 минут?

Какой угол (в градусах) описывает часовая стрелка за 3 часа 52 минуты?

Какой угол (в градусах) описывает часовая стрелка за 2 часа 48 минут?

Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?

Какой угол (в градусах) описывает часовая стрелка за 5 часов 58 минут?

Какой угол (в градусах) описывает часовая стрелка за 3 часа 30 минут?

Какой угол (в градусах) описывает часовая стрелка за 5 часов 30 минут?

Раздел 3.

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 20°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 24°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 25°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 29°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 9°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 21°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 28°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 5°?

На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 11°?

Раздел 4.

Найдите угол, который образуют минутная и часовая стрелки часов в 15:00. Ответ дайте в градусах

Найдите угол, который образуют минутная и часовая стрелки часов в 16:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 8:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 10:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 14:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 12:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 13:00. Ответ дайте в градусах.

Найдите угол, который образуют минутная и часовая стрелки часов в 7:00. Ответ дайте в градусах.

Раздел 5.

На сколько градусов повернётся Земля вокруг своей оси за 7 часов?

На сколько градусов повернётся Земля вокруг своей оси за 2 часа?

На сколько градусов повернётся Земля вокруг своей оси за 1 час?

На сколько градусов повернётся Земля вокруг своей оси за 5 часов?

На сколько градусов повернётся Земля вокруг своей оси за 8 часов?

На сколько градусов повернётся Земля вокруг своей оси за 6 часа?

На сколько градусов повернётся Земля вокруг своей оси за 7 часа?

Раздел 6.

За сколько часов Земля повернётся вокруг своей оси на 120⁰?

За сколько часов Земля повернётся вокруг своей оси на 45⁰?

За сколько часов Земля повернётся вокруг своей оси на 150⁰?

За сколько часов Земля повернётся вокруг своей оси на 75⁰?

За сколько часов Земля повернётся вокруг своей оси на 165⁰?

За сколько часов Земля повернётся вокруг своей оси на 90⁰?

Раздел 7.

На рисунке изображено колесо с пятью спицами.

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 12°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 10°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 40°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 9°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 15°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 45°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 18°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 30°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 24°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 14,4°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 36°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 60°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 20°?

Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 8°?

Раздел 8.

Колесо имеет 10 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 36 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 20 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 9 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 5 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 15 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 25 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 40 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 8 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 6 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 24 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 45 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Колесо имеет 30 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Теорема Пифагора.

Раздел 1.

Лестницу длиной 3 м прислонили к дереву. Найдите высоту, на которой находится её верхний конец, если нижний конец отстоит от ствола дерева на 1,8 м. Ответ дайте в метрах.

Лестницу длиной 3,7 м прислонили к дереву. Найдите высоту, на которой находится её верхний конец, если нижний конец отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.

Лестницу длиной 2 м прислонили к дереву. Найдите высоту, на которой находится её верхний конец, если нижний конец отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.

Лестницу длиной 2,5 м прислонили к дереву. Найдите высоту, на которой находится её верхний конец, если нижний конец отстоит от ствола дерева на 0,7 м. Ответ дайте в метрах.

Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м. Ответ дайте в метрах.

Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.

Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.

Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м. Ответ дайте в метрах.

Раздел 2.

Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 3 м. Длина троса равна 5 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Длина троса равна 10 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 3 м. Найдите длину троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 м от земли. Длина троса равна 4 м. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,8 м от земли. Длина троса равна 6 м. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Длина троса равна 3,9 м. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,8 м от земли. Длина троса равна 5 м. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 4,2 м. Длина троса равна 7 м. Найдите расстояние от земли до точки крепления троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,4 м от земли. Расстояние от основания флагштока

до места крепления троса на земле равно 3,3 м. Найдите длину троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса. Ответ дайте в метрах.

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 5 м. Найдите длину троса. Ответ дайте в метрах.

Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.

Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах.

Пожарную лестницу приставили к окну, расположенному на высоте 12 м от земли. Нижний конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.

Пожарную лестницу приставили к окну, расположенному на высоте 15 м от земли. Нижний конец лестницы отстоит от стены на 8 м. Какова длина лестницы? Ответ дайте в метрах.

Пожарную лестницу длиной 10 м приставили к окну третьего этажа дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.

Раздел 3.

От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.

От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.

От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода. Ответ дайте в метрах.

От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода. Ответ дайте в метрах.

От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м. Ответ дайте в метрах.

От столба высотой 9 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода. Ответ дайте в метрах.

Раздел 4.

Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?

Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 16 км/ч и 30 км/ч. Какое расстояние (в километрах) будет между ними через 1 час?

Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 21 км/ч и 28 км/ч. Какое расстояние (в километрах) будет между ними через 4 часа?

Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 18 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 5 часов?

Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 24 км/ч и 10 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?

Мальчик прошел от дома по направлению на восток 450 м. Затем повернул на север и прошел 240 м. На каком расстоянии (в метрах) от дома оказался мальчик?

Мальчик прошел от дома по направлению на восток 120 м. Затем повернул на север и прошел 50 м. На каком расстоянии (в метрах) от дома оказался мальчик?

Мальчик прошел от дома по направлению на восток 280 м. Затем повернул на север и прошел 450 м. На каком расстоянии (в метрах) от дома оказался мальчик?

Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Девочка прошла от дома по направлению на запад 420 м. Затем повернула на север и прошла 920 м. После этого она повернула на восток и прошла еще 420 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Подобие.

Раздел 1.

Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8,5 м. Тень человека равна 3,1 м. Какого роста человек (в метрах)?

Человек стоит на расстоянии 12 м от столба, на котором висит фонарь, расположенный на высоте 9,5 м. Тень человека равна 3 м. Какого роста человек (в метрах)?

Человек стоит на расстоянии 7,6 м от столба, на котором висит фонарь, расположенный на высоте 6 м. Тень человека равна 3,8 м. Какого роста человек (в метрах)?

Человек стоит на расстоянии 4,2 м от столба, на котором висит фонарь, расположенный на высоте 5 м. Тень человека равна 2,8 м. Какого роста человек (в метрах)?

Человек стоит на расстоянии 11,1 м от столба, на котором висит фонарь, расположенный на высоте 9 м. Тень человека равна 2,4 м. Какого роста человек (в метрах)?

На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м? На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).

Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).

Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?

На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?

Человек ростом 1,5 м стоит на расстоянии 13 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.

Человек ростом 1,9 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,6 м. Найдите длину тени человека в метрах.

Человек ростом 1,7 м стоит на расстоянии 9 м от столба, на котором висит фонарь на высоте 6,8 м. Найдите длину тени человека в метрах.

Человек ростом 1,8 м стоит на расстоянии 16 м от столба, на котором висит фонарь на высоте 16,2 м. Найдите длину тени человека в метрах.

Человек ростом 1,8 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 7,8 м. Найдите длину тени человека в метрах.

Человек ростом 1,5 м стоит на расстоянии 20 м от столба, на котором висит фонарь на высоте 4,5 м. Найдите длину тени человека в метрах.

Человек ростом 1,8 м стоит на расстоянии 13 м от столба, на котором висит фонарь на высоте 5,7 м. Найдите длину тени человека в метрах.

Человек ростом 1,6 м стоит на расстоянии 18 м от столба, на котором висит фонарь на высоте 6,4 м. Найдите длину тени человека в метрах.

Человек ростом 1,7 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 5,1 м. Найдите длину тени человека в метрах.

Раздел 2.

На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?

На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?

На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?

На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?

Раздел 3.

Проектор полностью освещает экран A высотой 140 см, расположенный на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 360 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 70 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 150 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 240 см, расположенный на расстоянии 300 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 80 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 110 см, расположенный на расстоянии 180 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 220 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 200 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 400 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 60 см, расположенный на расстоянии 110 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 210 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 140 см, расположенный на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 190 см, расположенный на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 100 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 150 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

Лестница. Ступеньки.

Лестница соединяет точки и и состоит из 50 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками и (в метрах).

Лестница соединяет точки и и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина — 28 см. Найдите расстояние между точками и (в метрах).

Лестница соединяет точки и и состоит из 50 ступеней. Высота каждой ступени равна 13 см, а длина — 84 см. Найдите расстояние между точками и (в метрах).

Лестница соединяет точки и и состоит из 20 ступеней. Высота каждой ступени равна 17,5 см, а длина — 60 см. Найдите расстояние между точками и (в метрах).

Лестница соединяет точки и и состоит из 35 ступеней. Высота каждой ступени равна 16 см, а длина — 30 см. Найдите расстояние между точками и (в метрах).

Лестница соединяет точки A и B. Высота каждой ступени равна 28 см, а длина — 96 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки A и B. Высота каждой ступени равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет 12,5 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки A и B. Высота каждой ступени равна 19,5 см, а длина — 40 см. Расстояние между точками A и B составляет 17,8 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки A и B. Высота каждой ступени равна 24 см, а длина — 70 см. Расстояние между точками A и B составляет 29,6 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки и . Высота каждой ступени равна 14 см, а длина — 48 см. Расстояние между точками и составляет 12,5 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки и . Высота каждой ступени равна 19,5 см, а длина — 40 см. Расстояние между точками и составляет 17,8 м. Найдите высоту, на которую поднимается лестница (в метрах).

Лестница соединяет точки A и B. Высота каждой ступени равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет 10 м. Найдите высоту, на которую поднимается лестница (в метрах).

Площадь.

Раздел 1.

Площадь прямоугольного земельного участка равна 11 га, ширина участка равна 100 м. Найдите длину этого участка в метрах.

Площадь прямоугольного земельного участка равна 20 га, ширина участка равна 200 м. Найдите длину этого участка в метрах.

Площадь прямоугольного земельного участка равна 18 га, ширина участка равна 240 м. Найдите длину этого участка в метрах.

Площадь прямоугольного земельного участка равна 10 га, ширина участка равна 100 м. Найдите длину этого участка в метрах.

Площадь прямоугольного земельного участка равна 13 га, ширина участка равна 260 м. Найдите длину этого участка в метрах.

Площадь прямоугольного земельного участка равна 6 га, ширина участка равна 200 м. Найдите длину этого участка в метрах.

Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1080 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

Картинка имеет форму прямоугольника со сторонами 20 см и 23 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1258 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

Картинка имеет форму прямоугольника со сторонами 23 см и 39 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1161 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

Картинка имеет форму прямоугольника со сторонами 29 см и 44 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 2106 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

Раздел 2.

Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?

Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?

Пол комнаты, имеющей форму прямоугольника со сторонами 5 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 40 см. Сколько потребуется таких дощечек?

Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 40 см. Сколько потребуется таких дощечек?

Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?

Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?

Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 4,4 м?

Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,8 м?

Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 3 м?

Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,2 м?

Разное

Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,2 м, высота большей опоры 2,7 м. Найдите высоту средней опоры.

Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры. Ответ дайте в метрах.

Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большой опоры. Ответ дайте
в метрах.

Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 2,2 м, высота большой опоры 2,5 м. Найдите высоту малой опоры. Ответ дайте в метрах.

Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота большой опоры 3,3 м. Найдите высоту малой опоры. Ответ дайте в метрах.

Ответы.

Раздел 4.

140

Подобие.

Раздел 1.

1,7

1,9

1,6

Раздел 2.

1,5

Раздел 3.

540

300

100

495

736

728

360

1600

385

570

420

300

Лестница. Ступеньки.

6,5

4,2

Площадь.

Раздел 1.

110

Раздел 2.

1440

4000

330

408

255

357

Разное

2,45

2,3

2,5

1,9

2,9

Источник

Источники:

Презентация по геометрии по подготовке к экзамену (№ 16)

Презентация по геометрии по подготовке к экзамену (№ 16).

ГИА — 2016 Открытый банк заданий по математике

Прямоугольный треугольник. Равносторонний треугольник

В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 300

Источники:

Материал по математике для подготовки к ОГЭ

Материал по математике для подготовки к ОГЭ

Просмотр содержимого документа «10Okrug_ixElementu»

Просмотр содержимого документа «11PlogadiFigur»

Просмотр содержимого документа «12Figuru_na kvadratRecetke»

Просмотр содержимого документа «13Geometric_Vuskazuvania»

Просмотр содержимого документа «14Analiz_DiagramTablisGrafikov (1)»

Просмотр содержимого документа «14Analiz_DiagramTablisGrafikov»

Просмотр содержимого документа «16Prost_Tekst_Zadaci»

Просмотр содержимого документа «17Praktic_ZadaciPOGeometrii»

Просмотр содержимого документа «18Analiz_Diagram»

Источники:

Вместе с этой задачей также решают:

Просмотр содержимого документа
«10Okrug_ixElementu»

Просмотр содержимого документа
«11PlogadiFigur»

Просмотр содержимого документа
«12Figuru_na kvadratRecetke»

Просмотр содержимого документа
«13Geometric_Vuskazuvania»

Просмотр содержимого документа
«14Analiz_DiagramTablisGrafikov (1)»

Просмотр содержимого документа
«14Analiz_DiagramTablisGrafikov»

Просмотр содержимого документа
«16Prost_Tekst_Zadaci»

Просмотр содержимого документа
«17Praktic_ZadaciPOGeometrii»

Просмотр содержимого документа
«18Analiz_Diagram»