Новый октябрьский тренировочный вариант (тренировочная работа) №37812191 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812191:
Ответы и решения:
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1).
Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Задание 1 № 413030 Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Ответ: 56,4
Задание 2 № 413031 Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Ответ: 8070
Задание 3 № 413032 Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
Ответ: 62,5
Задание 4 № 413033 Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Ответ: 9813
Задание 5 № 413034 Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Ответ: 13
Задание 7 № 314789 На координатной прямой отмечены числа а и с. Какое из следующих утверждений неверно? В ответе укажите номер выбранного варианта.
Ответ: 1
Задание 10 № 132734 В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Ответ: 0,2
Задание 14 № 393942 Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Ответ: 8
Задание 15 № 132774 Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 70
Задание 16 № 356618 Хорды AC и BD окружности пересекаются в точке P, BP=15, CP = 6, DP = 10. Найдите AP.
Ответ: 25
Задание 17 № 323957 Найдите площадь ромба, если его диагонали равны 14 и 6.
Ответ: 42
Задание 19 № 93 Укажите номера верных утверждений. 1) Существует квадрат, который не является прямоугольником. 2) Если два угла треугольника равны, то равны и противолежащие им стороны. 3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Ответ: 23
Задание 21 № 311600 Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Ответ: 400 км
Задание 23 № 339619 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Ответ: 42
Задание 24 № 340104 Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и T соответственно. Докажите, что BP = DT.
Задание 25 № 340129 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)
Обсуждение
gimmegun
12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06
Одной из причин может быть выбор фильтров
По спискам
и
По типу
при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры
Избранное
и
Все.
Если выбраны
Все
и
Все
, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры
Все
и
Все
.
Другой причиной может быть то, что задание выключено или забанено.
Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…
Для обсуждения вопроса/идеи необходима регистрация.
crsun148
Вопрос по математике:
Помогите номер 16 пожалуйста
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 2
kledincrdr988
730-это 100%
803-это 803:730*100%= 110%
110%-100%=10(%)-увеличивалось число жителей
wakns804
Было 730 жителей_это 10 %
803 это 803:730*100=110%
Значит 110-100=10%-Увеличилось число жителей
Ответ:на 10%
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
4
1 ответ:
0
0
236+580=816 км
1200-816=384 км
Ответ: между ними стало 384 км
Читайте также
1) 15*3=45 кустов рябины посадили до обеда
2)15+45=60 кустов рябины и акации посадили до обеда
3) 90-60=30 кустов акации и рябины осталось посадить после обеда
Ответ: 30 кустов
Он понимает что он слуга.
Ответ: В главе Княжна Мери Печорина показывают как хитрого и эгоистичного, наплевавшего на чувства окружающих человека. Однако не бывает идеально хороших или плохих людей. Печорин увивался за княжной Мери только по прозьбе Веры, к которой у него до сих пор остались чувства
Объяснение:
Про твою школу надо рассказать?
Ледуя своим «прогрессивным» идеям, Базаров пытается
относиться к женщинам с циничной насмешкой. Для него
«природа не храм, а мастерская, и человек в ней — работник. »
Красота, искусства, любовь для него — пустые слова.
Но природа берет своё, и он с ужасом убеждается, что
влюбился в Одинцову. Огромным усилием воли ему удаётся
преодолеть эту привязанность («лучше камни бить на мостовой,
чем позволить женщине завладеть хотя бы кончиком пальца»).
Но что-то в его душе надломилось, и его неосторожность при
вскрытии умершего и гибель от заражения были, может быть,
не случайны. Базаров был нигилист, т. е. отрицал всё, в том числе и любовь. Поэтому и с Одинцовой ничего у него не вышло. То есть отношение к женщинам было б<span>езразличное, он «лишний человек» и проецирует свои комплексы на окружающих ему женщинах, принося им одни несчастья.
</span><span> Аркадий Кирсанов вырос, имея перед глазами живой пример нежной и глубокой любви родителей. Именно поэтому он так возмущался, когда его друг — нигилист Базаров — высмеивал человеческие чувства, таинственность отношений мужчины и женщины, «загадочность» женского взгляда. Стоило ему отдалиться от Евгения, как потребность в близком и любящем его человеке стала ведущей, и Катя вошла в его жизнь долгожданным светом. В отношениях Аркадия и Кати Одинцовой И. С. Тургенев разоблачает нигилистские взгляды Аркадия. Катя заявляет, что переделает его и претворяет свои слова в жизнь. Кирсанов отказывается от своей прошлой идеологии. По сути, любовь Аркадия к Кате результат подчинения слабой натуры более сильной. Наиболее яркая история любви случилась в романе у Евгения Базарова. Умный, рассудительный, живущий головой, а не сердцем, он не оставлял в своей жизни места для чувств, поскольку считал их чепухой, выдумкой, неспособностью следовать своим убеждениям. Именно по этому любовь застала его врасплох, смяла, привела в отчаяние. Как мог он, Базаров, попасться на эту удочку, если всегда смеялся над этим чувством, которому просто не давал права на существование! Но оно пришло и сделало образ Базарова трагическим, поскольку, возвысив его, не только заставило усомниться в своих установках и убеждениях, но и сделало его более человечным. В обществе Одинцовой он резок, насмешлив, а наедине с собой открывает в себе романтика. Его раздражают собственные чувства. И когда они, наконец, выливаются, то приносят только страдания. Избранница отвергла Базарова, испугавшись его животной страсти и безкультурия чувств. Она не может пожертвовать своим порядком, ей нужна спокойная любовь. Тургенев подаёт жестокий урок своему герою. Но Базарова любовь не погубила, за счет своего характера он не сдался, жизнь на этом не закончилась.</span>
Для таблицы на рис. 13
постройте следующие виды сводных таблиц:
• по учебным
группам подведите итоги по каждому
предмету и виду занятий с привязкой
к преподавателю:
средний балл;
количество оценок;
минимальная
оценка;
максимальная
оценка;
• по каждому
преподавателю подведите итоги в разрезе
предметов и номеров учебных групп:
количество оценок;
средний балл;
структура
успеваемости.
Технология работы
1. Проведите
подготовительную работу:
-
откройте
созданную рабочую книгу Spisok
командой Файл, Открыть; -
вставьте новый
лист и назовите его Свод; -
выделите блок
ячеек исходного списка на листе Список,
начиная от имен полей и вниз до конца
записей таблицы, и скопируйте их на
лист Свод.
2. Создайте сводную
таблицу с помощью Мастера сводных таблиц
по шагам:
-
установите курсор
в области данных таблицы; -
выполните команду
Данные, Сводная таблица.
Этап
1 — выберите источник данных — текущую
таблицу, щелкнув по кнопке <в списке
или базе данных Ехсеl>
и по кнопке <Далее>.
Этап 2 — в строке
Диапазон должен быть отображен блок
ячеек списка (базы данных). Если
диапазон указан неверно, то надо его
стереть и с помощью мыши выделить нужный
блок ячеек.
Этап 3 — постройте
макет сводной таблицы так, как показано
на рис.3.50. Технология построения
будет одинаковой для всех структурных
элементов и будет состоять в следующем:
-
подведите курсор
к имени поля, находящегося в правой
стороне макета; -
нажмите левую
кнопку мыши и, удерживая ее нажатой,
перетащите элемент с именем поля в одну
из областей (Страница, Строка, Столбец,
Данные); -
отпустите кнопку
мыши, поле должно остаться в этой
области; -
после установки
поля в области Данные необходимо два
раза щелкнуть по нему правой кнопкой
мыши и в диалоговом окне «Вычисление
поля сводной таблицы» выбрать операцию
(функцию) над значением поля.
Этап 4 — выбор
места расположения — существующий
лист.
-
Выполните
автоформатирование полученной сводной
таблицы командой Формат, Автоформат. -
Внесите изменения
в исходные данные и выполните команду
Данные, Обновить данные. -
Повторите процесс
построения сводной таблицы для п.2
задания.
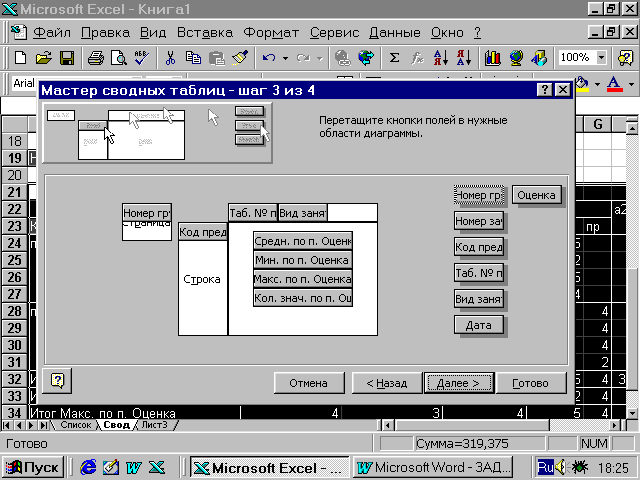
Рис. 18. Пример
макета сводной таблицы
Задание-17
Консолидация данных
по расположению и по категориям.
-
откройте
книгу Spisok,
вставьте два листа и переименуйте
их. -
Создайте на
листе Консол.распол. таблицу расчета
заработной платы (за январь). -
Скопируйте
созданную таблицу на тот же лист,
измените в ней данные. Эта таблица
будет отражать уровень заработной
платы за февраль. -
Выполните
консолидацию данных по расположению
и сравните результат с рис. 19. -
Скопируйте обе
таблицы (заработная плата за январь
и за февраль) с листа Консол.распол.
на лист Консол.категор и измените
вторую таблицу в соответствии с
рис.20.
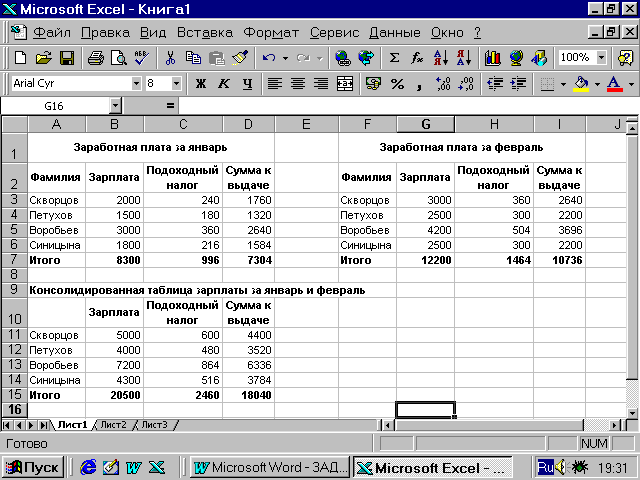
Рис.19. Пример
консолидации данных по расположению
-
Выполните
консолидацию данных по категориям и
сравните результат с рис. 20.
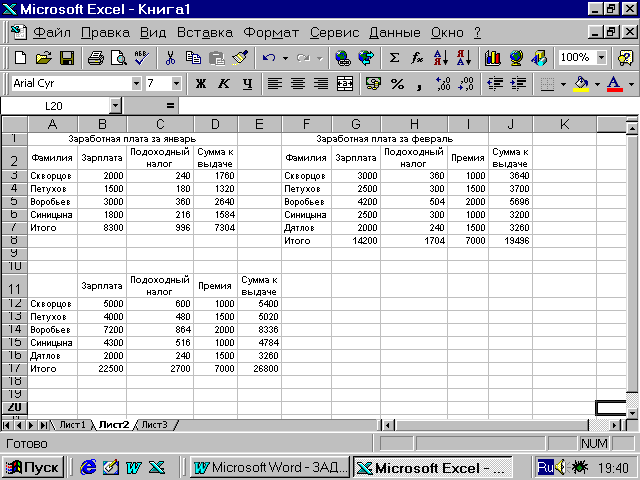
Рис.20. Пример
консолидации данных по категориям
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Условие
vk209029450
2020-01-22 19:31:30
Как решить задания под номером 16 и 17?
предмет не задан
251
О решение…
На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.
Что Вы можете сделать?
- Выставите данный вопрос вновь. Перейдите на главную страницу.
- Найдите похожую задачу. Используйте поиск.
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Прототипы заданий 16 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 16 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (окружность, круг и их элементы)
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 16 с ответамиИсточник: math100.ru → скачать |
| Прототипы задания 16 ОГЭ по математике (окружности) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 16 Автор: Е. А. Ширяева → теория → задания |
| Задания 16 — практика → Скачать вариант 1 → Скачать ответы 1 → Скачать вариант 2 → Скачать ответы 2 |
Решение типовых задач № 16 на ОГЭ по математике
Связанные страницы:
Задание 15 ОГЭ по математике — треугольники, четырёхугольники, многоугольники и их элементы
Задание 13 ОГЭ по математике — неравенства
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 14 ОГЭ по математике — задачи на прогрессии
Хорды AC и BD окружности пересекаются в точке P, BP = 15, CP = 6, DP = 10. Найдите AP.
ПОДЕЛИТЬСЯ
Новый октябрьский тренировочный вариант (тренировочная работа) №37812191 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812191:
Ответы и решения:
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1).
Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Задание 1 № 413030 Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Ответ: 56,4
Задание 2 № 413031 Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Ответ: 8070
Задание 3 № 413032 Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
Ответ: 62,5
Задание 4 № 413033 Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Ответ: 9813
Задание 5 № 413034 Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Ответ: 13
Задание 7 № 314789 На координатной прямой отмечены числа а и с. Какое из следующих утверждений неверно? В ответе укажите номер выбранного варианта.
Ответ: 1
Задание 10 № 132734 В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Ответ: 0,2
Задание 14 № 393942 Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Ответ: 8
Задание 15 № 132774 Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 70
Задание 16 № 356618 Хорды AC и BD окружности пересекаются в точке P, BP=15, CP = 6, DP = 10. Найдите AP.
Ответ: 25
Задание 17 № 323957 Найдите площадь ромба, если его диагонали равны 14 и 6.
Ответ: 42
Задание 19 № 93 Укажите номера верных утверждений. 1) Существует квадрат, который не является прямоугольником. 2) Если два угла треугольника равны, то равны и противолежащие им стороны. 3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Ответ: 23
Задание 21 № 311600 Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Ответ: 400 км
Задание 23 № 339619 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Ответ: 42
Задание 24 № 340104 Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и T соответственно. Докажите, что BP = DT.
Задание 25 № 340129 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:
Значит, им понадобится
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.
Площадь заказника равна:
Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения:
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:
Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из приведенных утверждений неверно?
1)
2)
3)
4)
Решение.
Заметим, что и Проверим все варианты ответа:
1) — неверно;
2) — верно;
3) — верно;
4) — верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения
1)
2)
3)
4)
Решение.
Последовательно получим:
Ответ: 1
9. Задание 9 № 338500
При каком значении значения выражений и равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение Решим его:
Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.
1) функция возрастает на промежутке
2)
3)
4) прямая пересекает график в точках и
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .
2) — неверно,
3) — верно, видно из графика.
4) Прямая пересекает график в точках и — верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .
Решение.
Выразим :
Подставляя, получаем:
Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:
Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:
Ответ: 377 мест.
15. Задание 15 № 340000
В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите
Решение.
Из прямоугольного треугольника по теореме Пифагора найдём
Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
Ответ: 0,2.
16. Задание 16 № 351463
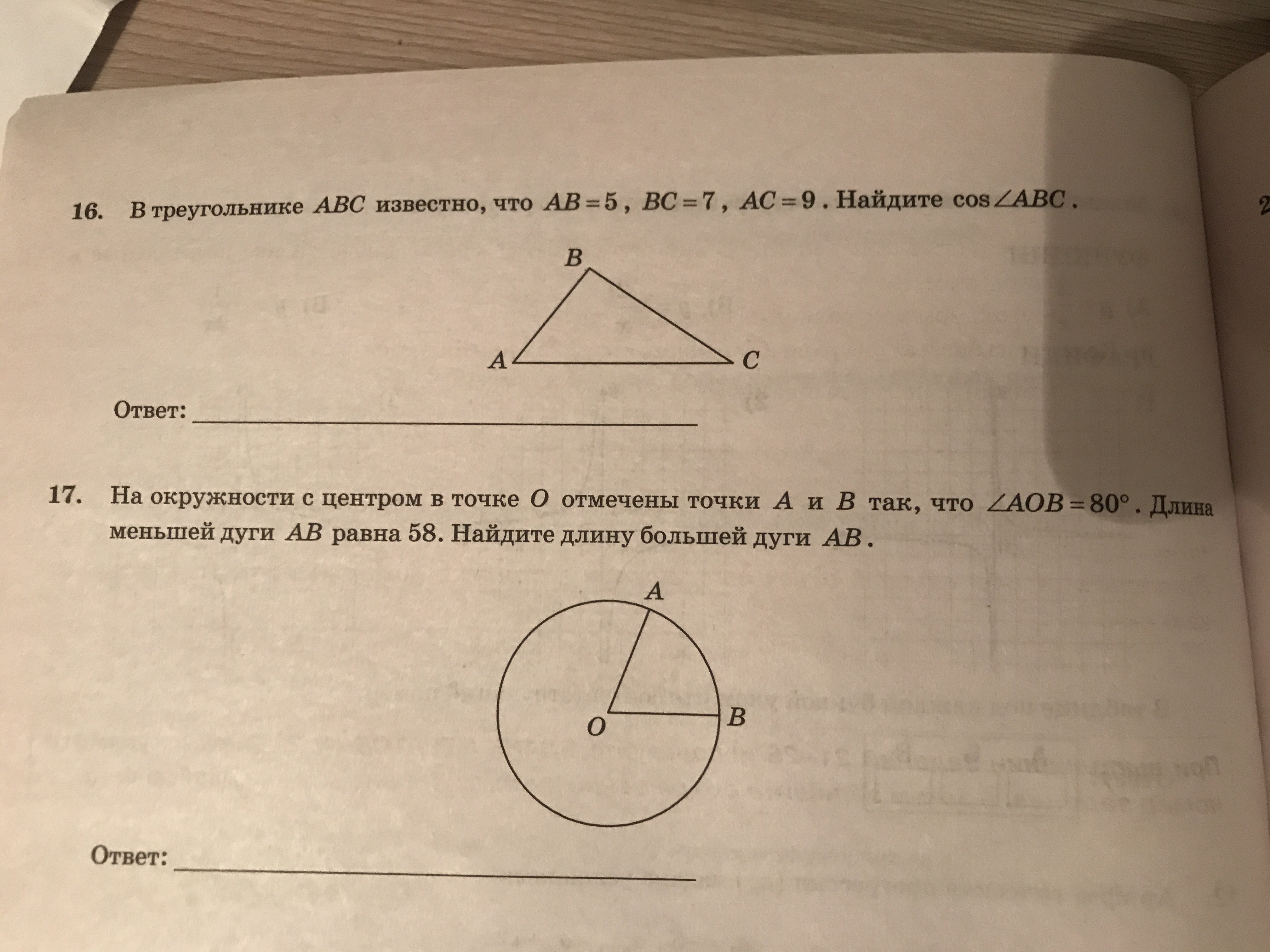
На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842
Найдите угол
Решение.
Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение
Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ
Ответ:
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:
График функции сводится к графику параболы с выколотой точкой
Выделим полный квадрат:
Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)
Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и
Ответ: 16.
24. Задание 24 № 155
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.
По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,
Площадь трапеции :
Площадь трапеции
Ответ: 9.
| 3568 | Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠BB1C1 = ∠BAH. б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1=9 и ∠BAC = 60° Решение | Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠BB1C1 = ∠BAH ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 16 Вариант МА2210209 | |
| 3532 | На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно. Около четырёхугольников AKND и BCNK также можно описать окружность. Косинус одного из углов четырёхугольника ABCD равен 0,25. а) Докажите, что четырёхугольник ABCD является равнобедренной трапецией. б) Найдите радиус окружности, описанной около четырёхугольника AKND, если радиус окружности, описанной около четырёхугольника ABCD, равен 8, AK:KB = 2:5, а BC < AD и BC = 4 Решение | На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 16 | |
| 3514 | Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F соответственно. Точка D — основание высоты, опущенной из вершины C. I и J — центры окружностей, вписанных в треугольники BCD и ACD. а) Докажите, что I и J лежат на отрезке EF. б) Найдите расстояние от точки C до прямой IJ, если AC=15, BC=20 Решение | Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 16 | |
| 3502 | В трапеции ABCD с меньшим основанием BC точки E и F — середины сторон ВC и AD соответственно. В каждый из четырёхугольников ABEF и ECDF можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Найдите радиус окружности, описанной около трапеции ABCD, если AB=7, а радиус окружности, вписанной в четырёхугольник ABEF, равен 2,5 Решение | В трапеции ABCD с меньшим основанием BC точки E и F — середины сторон ВC и AD соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 16 | |
| 3492 | Четырёхугольник ABCD со сторонами BC=7 и AB=CD=20 вписан в окружность радиусом R=16. а) Докажите, что прямые BC и AD параллельны. б) Найдите AD Решение | Четырёхугольник ABCD со сторонами BC=7 и AB=CD=20 вписан в окружность радиусом R=16 ! 36 вариантов ФИПИ Ященко 2023 Вариант 3 Задание 16 | |
| 3490 | Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки F и E так, что FE параллельно CD, a FC=ED. а) Докажите, что угол BCF равен углу AFE. б) Найдите площадь трапеции ABCD, если DE=5BF, FE=8 и площадь трапеции FCDE равна 27sqrt11 Решение | Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки F и E так, что FE параллельно CD, a FC=ED ! Досрочный ЕГЭ 2022 по математике 28.03.2022 Задание 16 | |
| 3477 | В параллелограмме ABCD угол ВАС вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE=CE. а) Докажите, что AL:BC=AB:BC. б) Найдите EL, если AC=21, tg /_BCA=0,4 Решение | В параллелограмме ABCD угол ВАС вдвое раза больше угла CAD ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 16 # ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 16 Санкт-Петербург, Центр # Задача-Аналог 3356 | |
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN Решение | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ Решение | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3460 | Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. а) Докажите, что прямые АС и BD параллельны. б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1 Решение | Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А ! Тренировочный вариант 397 от Ларина Задание 16 # Задача-Аналог 762 | |
Показать ещё…
Показана страница 1 из 34
Решение заданий варианта №16 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
![]()
Задание 1-5.
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт·ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт · ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт · ч электроэнергии в рублях в 2021 году.

В квартире у Петра Сергеевича установлен трёхтарифный счётчик, и в 2021 году Николай Андреевич оплачивал электроэнергию по трёхтарифному учёту.
На рисунке точками показан расход электроэнергии в квартире Петра Сергеевича по тарифным зонам за каждый месяц 2021 года. Для наглядности точки соединены линиями.
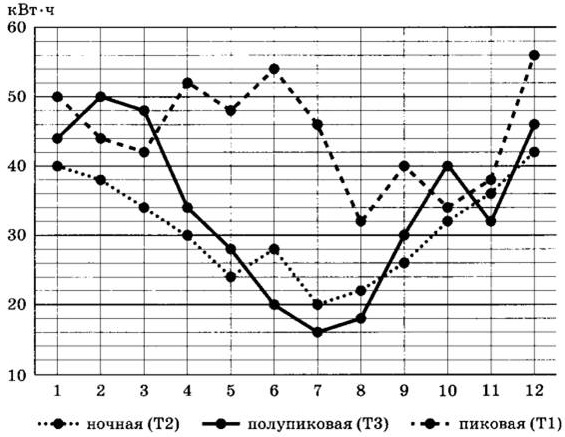
Задание 6.
Найдите значение выражения (frac{2}{15}+frac{5}{12})cdot frac{16}{11}.
Задание 7.
На координатной прямой точки А, В, С и D соответствуют числам -frac{1}{50}; frac{1}{50}; -frac{11}{15}; -frac{11}{50}.
![]()
Какой точке соответствует число -frac{11}{50}?
1) A 2) B 3) C 4) D
Задание 8.
Найдите значение выражения 9√7·2√2·√14.
Задание 9.
Решите уравнение x2 – 4 = 2x – 1.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,14. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
А) y=frac{1}{6x}
Б) y=-frac{6}{x}
В) y=frac{6}{x}
ГРАФИКИ
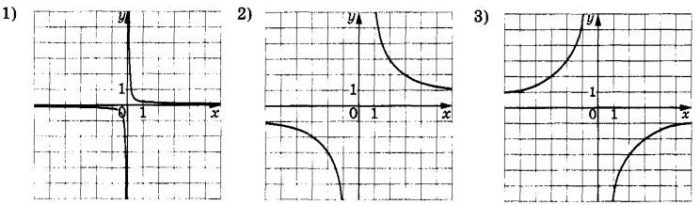
В таблице под буквой укажите соответствующий номер.
Задание 12.
Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи её поверхности вычисляется по формуле Е = mgh, где m – масса тела (в килограммах), g – ускорение свободного падения (в м/с2), a h – высота (в метрах), на которой находится это тело, относительно поверхности. Пользуясь этой формулой, найдите m (в килограммах), если g = 9,8 м/с2, h = 5 м, а E = 196 Дж.
Задание 13.
Укажите неравенство, решение которого изображено на рисунке.
![]()
1) x2 – 16 ≤ 0
2) x2 – 4x ≤ 0
3) x2 – 4x ≥ 0
4) x2 – 16 ≥ 0
Задание 14.
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.
![]()
Задание 15.
В треугольнике ABC угол С равен 90°, М – середина стороны АВ, АВ = 64, ВС = 44. Найдите СМ.
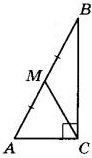
Задание 16.
Касательные в точках A и В к окружности с центром в точке О пересекаются под углом 56°. Найдите угол АВО. Ответ дайте в градусах.
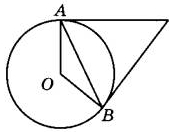
Задание 17.
Высота равнобедренной трапеции, проведённая из вершины С, делит основание AD на отрезки длиной 8 и 17. Найдите длину основания ВС.
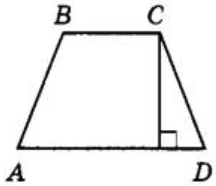
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
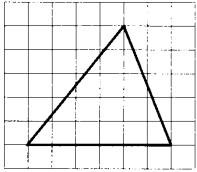
Задание 19.
Какое из следующих утверждений верно?
1) Диагонали ромба равны.
2) Отношение площадей подобных треугольников равно коэффициенту подобия.
3) В треугольнике против большего угла лежит большая сторона.
В ответ запишите номер выбранного утверждения.
ЧАСТЬ 2
![]()
Задание 20.
Решите систему уравнений begin{cases} x^{2}+y^{2}=65, \ xy=8. end{cases}
Задание 21.
Первый рабочий за час делает на 6 деталей больше, чем второй, и выполняет заказ, состоящий из 140 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Задание 22.
Постройте график функции y=frac{7x-6}{7x^{2}-6x}.
Определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
![]()
Задание 23.
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 14, DC = 30, АС = 39.
Задание 24.
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
Задание 25.
В равнобедренную трапецию, периметр которой равен 20, а площадь равна 20, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.










 пачек чая.
пачек чая.

 км.
км. руб.
руб.






 и
и  Проверим все варианты ответа:
Проверим все варианты ответа:






 значения выражений
значения выражений  и
и  равны?
равны? Решим его:
Решим его:

 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.



 пересекает график в точках
пересекает график в точках  и
и 
 и затем возрастает на
и затем возрастает на  .
. — неверно,
— неверно, 

 — верно, видно из графика.
— верно, видно из графика. пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика. , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
. :
:







 катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
 по теореме Пифагора найдём
по теореме Пифагора найдём 

 и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги. равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
 .
.


 часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 






 г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%. И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку. равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:
 с выколотой точкой
с выколотой точкой 

 сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)
 имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 


 следовательно, треугольники
следовательно, треугольники  равны. Так как
равны. Так как  =
=  треугольники
треугольники  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
 :
: 



