Решу огэ математика 356379
Задание 15 № 341708
Основания трапеции равны 3 и 13. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.
Задание 15 № 341708
Пусть KN средняя линия трапеции, где L точка пересечения с диагональю.
Oge. sdamgia. ru
27.04.2019 11:51:28
2019-04-27 11:51:28
Источники:
Https://oge. sdamgia. ru/problem? id=341708
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу огэ математика 356379
Решу огэ математика 356379
Решу огэ математика 356379
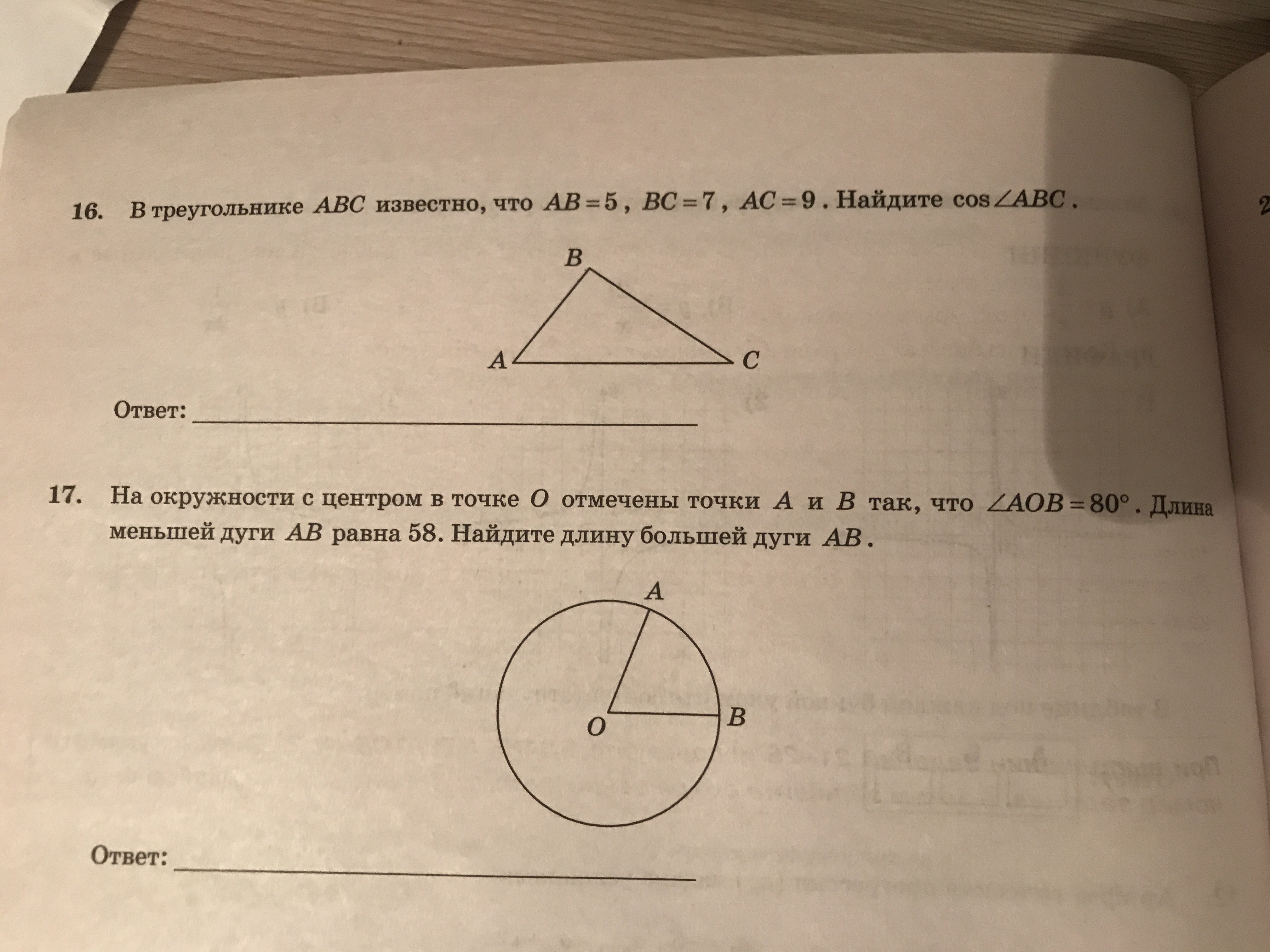
Задание 16 № 356478
Сторона равностороннего треугольника равна Найдите радиус окружности, описанной около этого треугольника.
Треугольник ABC правильный, значит, все его углы равны по 60°. По теореме синусов: значит
Приведем решение с использованием приведенной в справочных материалах к экзамену формулы, связывающей сторону равностороннего треугольника и радиус описанной окружности:
Задание 16 № 324868
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Заметим, что длины дуг относятся так же, как их градусные меры. Пусть первая дуга имеет градусную меру тогда вторая дуга имеет градусную меру а третья — Три дуги в сумме составляют окружность, поэтому получаем:
Поэтому меньшая дуга окружности равна Угол треугольника, опирающийся на эту дугу является вписанным, поэтому он равен половине дуги: Меньший угол треугольника лежит против меньшей стороны. Найдём радиус описанной окружности:
Задание 16 № 356478
Задание 16 № 324868
Поэтому меньшая дуга окружности равна Угол треугольника, опирающийся на эту дугу является вписанным, поэтому он равен половине дуги Меньший угол треугольника лежит против меньшей стороны.
Oge. sdamgia. ru
02.02.2020 22:48:40
2020-02-02 22:48:40
Источники:
Https://oge. sdamgia. ru/test? theme=35&sort=hard
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу огэ математика 356379
Решу огэ математика 356379
Решу огэ математика 356379
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
Объекты
| Коридор | Кладовая | Спальня | Гостиная |
Цифры
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Плитка для пола размером 40 см на 40 см продаётся в упаковках по 12 штук. Сколько упаковок плитки понадобится, чтобы выложить пол санузла?
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Найдите площадь санузла. Ответ дайте в квадратных метрах.
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
На сколько процентов площадь коридора больше площади кладовой?
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой, не превосходящую 85 см по высоте.
МодельВместимость барабана (кг)Тип загрузкиСтоимость (руб.)Стоимость подключения (руб.)Стоимость доставки (% от стоимости машины)Габариты (высота × ширина × глубина, см)
| А | 7 | Верт. | 28 000 | 1700 | Бесплатно | 85 × 60 × 45 |
| Б | 5 | Фронт. | 24 000 | 4500 | 10 | 85 × 60 × 40 |
| В | 5 | Фронт. | 25 000 | 5000 | 10 | 85 × 60 × 40 |
| Г | 6,5 | Фронт. | 24 000 | 4500 | 10 | 85 × 60 × 44 |
| Д | 6 | Фронт. | 28 000 | 1700 | Бесплатно | 85 × 60 × 45 |
| Е | 6 | Верт. | 27 600 | 2300 | Бесплатно | 89 × 60 × 40 |
| Ж | 6 | Верт. | 27 585 | 1900 | 10 | 89 × 60 × 40 |
| З | 6 | Фронт. | 20 000 | 6300 | 15 | 85 × 60 × 42 |
| И | 5 | Фронт. | 27 000 | 1800 | Бесплатно | 85 × 60 × 40 |
| К | 5 | Верт. | 27 000 | 1800 | Бесплатно | 85 × 60 × 40 |
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Слева от входа в квартиру находится санузел, а в противоположном конце коридора дверь в кладовую.
Math-oge. sdamgia. ru
07.07.2020 15:46:01
2020-07-07 15:46:01
Источники:
Https://math-oge. sdamgia. ru/test? id=37812193
Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)
Обсуждение
gimmegun
12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06
Одной из причин может быть выбор фильтров
По спискам
и
По типу
при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры
Избранное
и
Все.
Если выбраны
Все
и
Все
, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры
Все
и
Все
.
Другой причиной может быть то, что задание выключено или забанено.
Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…
Для обсуждения вопроса/идеи необходима регистрация.
2
ПОМОГИТЕ ПОЖАЛУЙСТА
задание номер 179
1 ответ:
0
0
1) <span> это разделы грамматики русского языка.
2) это члены предложения
3) буквы
4) знаки препинания
</span>
Читайте также
Не с наречием пишется слитно, т.к. можно заменить синонимом или близким по значению выражением
Всё, что сердцу дорого,
В песню так и просится.
И рассвет малиновый,
И под небом рощица.
Поглядишь с пригорочка —
Видно речку синюю,
Видно даль бескрайнюю,
<span>Что зовут Россиею.</span>
1. Зима — одно из времен года. 2. Во время зимних каникул я люблю проводить время с друзьями. 3. Мы катаемся на лыжам, коньках, санках, играем в снежки. 4. Иногда мы лепим снеговика. 5. В холодную зимнюю погоду я сижу дома и читаю книги.
Лес-подлежащее
Воздух,собиратель,источник-сказуемые,кстати,перед «собиратель» и «животворный» должна быть запятая
чистый,животворный,-дополнения
влаги,живого,всего-дополнения
Тетрадь по русскому языку
ученика(цы)класса 5 …
школы номер ….
ФИО….
пожалуйст прочитай то что я тебе передал плииииз
Для таблицы на рис. 13
постройте следующие виды сводных таблиц:
• по учебным
группам подведите итоги по каждому
предмету и виду занятий с привязкой
к преподавателю:
средний балл;
количество оценок;
минимальная
оценка;
максимальная
оценка;
• по каждому
преподавателю подведите итоги в разрезе
предметов и номеров учебных групп:
количество оценок;
средний балл;
структура
успеваемости.
Технология работы
1. Проведите
подготовительную работу:
-
откройте
созданную рабочую книгу Spisok
командой Файл, Открыть; -
вставьте новый
лист и назовите его Свод; -
выделите блок
ячеек исходного списка на листе Список,
начиная от имен полей и вниз до конца
записей таблицы, и скопируйте их на
лист Свод.
2. Создайте сводную
таблицу с помощью Мастера сводных таблиц
по шагам:
-
установите курсор
в области данных таблицы; -
выполните команду
Данные, Сводная таблица.
Этап
1 — выберите источник данных — текущую
таблицу, щелкнув по кнопке <в списке
или базе данных Ехсеl>
и по кнопке <Далее>.
Этап 2 — в строке
Диапазон должен быть отображен блок
ячеек списка (базы данных). Если
диапазон указан неверно, то надо его
стереть и с помощью мыши выделить нужный
блок ячеек.
Этап 3 — постройте
макет сводной таблицы так, как показано
на рис.3.50. Технология построения
будет одинаковой для всех структурных
элементов и будет состоять в следующем:
-
подведите курсор
к имени поля, находящегося в правой
стороне макета; -
нажмите левую
кнопку мыши и, удерживая ее нажатой,
перетащите элемент с именем поля в одну
из областей (Страница, Строка, Столбец,
Данные); -
отпустите кнопку
мыши, поле должно остаться в этой
области; -
после установки
поля в области Данные необходимо два
раза щелкнуть по нему правой кнопкой
мыши и в диалоговом окне «Вычисление
поля сводной таблицы» выбрать операцию
(функцию) над значением поля.
Этап 4 — выбор
места расположения — существующий
лист.
-
Выполните
автоформатирование полученной сводной
таблицы командой Формат, Автоформат. -
Внесите изменения
в исходные данные и выполните команду
Данные, Обновить данные. -
Повторите процесс
построения сводной таблицы для п.2
задания.
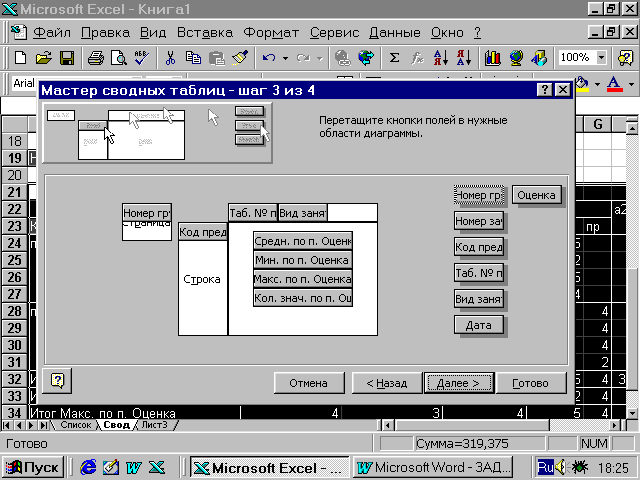
Рис. 18. Пример
макета сводной таблицы
Задание-17
Консолидация данных
по расположению и по категориям.
-
откройте
книгу Spisok,
вставьте два листа и переименуйте
их. -
Создайте на
листе Консол.распол. таблицу расчета
заработной платы (за январь). -
Скопируйте
созданную таблицу на тот же лист,
измените в ней данные. Эта таблица
будет отражать уровень заработной
платы за февраль. -
Выполните
консолидацию данных по расположению
и сравните результат с рис. 19. -
Скопируйте обе
таблицы (заработная плата за январь
и за февраль) с листа Консол.распол.
на лист Консол.категор и измените
вторую таблицу в соответствии с
рис.20.
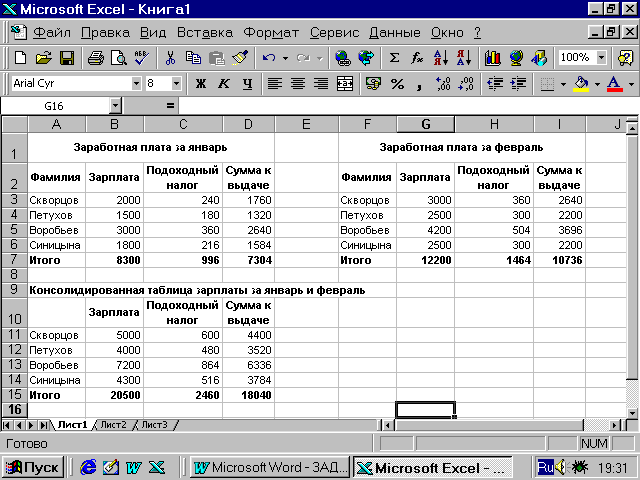
Рис.19. Пример
консолидации данных по расположению
-
Выполните
консолидацию данных по категориям и
сравните результат с рис. 20.
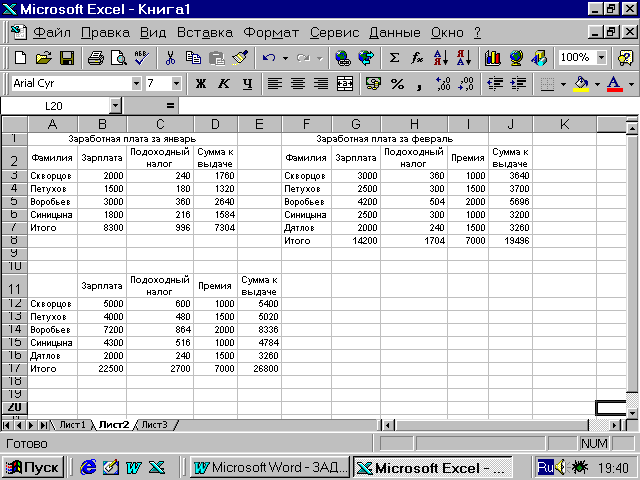
Рис.20. Пример
консолидации данных по категориям
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Условие
vk209029450
2020-01-22 19:31:30
Как решить задания под номером 16 и 17?
предмет не задан
245
О решение…
На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.
Что Вы можете сделать?
- Выставите данный вопрос вновь. Перейдите на главную страницу.
- Найдите похожую задачу. Используйте поиск.
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Практические задачи с ответами для задания №16 ОГЭ 2022 по математике для 9 класса, центральный и вписанный угол, касательная, хорда, секущая, радиус, окружность, описанная вокруг многоугольника решу ОГЭ онлайн на сайте.
Скачать задание 16 с ответами
Задание 16 ОГЭ 2022 математика 9 класс с ответами окружность:
1)Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 39°. Ответ дайте в градусах.
Ответ: 19,5
2)Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 64°. Ответ дайте в градусах.
Ответ: 32
3)Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 25°. Найдите угол AOD. Ответ дайте в градусах.
Ответ: 130
4)Отрезки AC и BD – диаметры окружности с центром О. Угол ACB равен 28°. Найдите угол AOD. Ответ дайте в градусах.
Ответ: 124
5)В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 40°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Ответ: 70
6)В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 38°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Ответ: 71
7)На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
Ответ: 54
8)На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что NBA = 42°. Найдите угол NMB. Ответ дайте в градусах.
Ответ: 48
9)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 56° и OAB = 15°. Найдите угол BCO. Ответ дайте в градусах.
Ответ: 41
10)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 62° и OAB = 53°. Найдите угол BCO. Ответ дайте в градусах.
Ответ: 9
11)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ABC = 76°. Найдите величину угла BOC. Ответ дайте в градусах.
Ответ: 104
12)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ABC = 57°. Найдите величину угла BOC. Ответ дайте в градусах.
Ответ: 123
13)Четырёхугольник ABCD вписан в окружность. Угол ABC равен 100°, угол CAD равен 31°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 69
14)Четырёхугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 29°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 76
15)Четырёхугольник ABCD вписан в окружность. Угол ABD равен 10°, угол CAD равен 62°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 72
16)Четырёхугольник ABCD вписан в окружность. Угол ABD равен 12°, угол CAD равен 71°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 83
17)На окружности с центром O отмечены точки A и B так, что AOB = 45°. Длина меньшей дуги AB равна 10. Найдите длину большей дуги
Ответ: 70
18)На окружности с центром O отмечены точки A и B так, что AOB = 30°. Длина меньшей дуги AB равна 12. Найдите длину большей дуги.
Ответ: 132
19)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 25°. Ответ дайте в градусах.
Ответ: 65
20)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 27°. Ответ дайте в градусах.
Ответ: 63
21)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 2,5. Найдите AC, если BC = 3.
Ответ: 4
22)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 12,5. Найдите AC, если BC = 7.
Ответ: 24
23)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC = 24.
Ответ: 18
24)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20,5. Найдите BC, если AC = 9.
Ответ: 40
25)Точка О – центр окружности, ACB = 75°. Найдите величину угла BOA (в градусах).
Ответ: 150
26)Точка О – центр окружности, ACB = 60°. Найдите величину угла BOA (в градусах).
Ответ: 120
27)Центральный угол AOB опирается на хорду AB длиной 11. При этом угол OAB равен 60°. Найдите радиус окружности.
Ответ: 11
28)Центральный угол AOB опирается на хорду AB длиной 17. При этом угол OAB равен 60°. Найдите радиус окружности.
Ответ: 17
29)Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол OAB. Ответ дайте в градусах.
Ответ: 60
30)Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 120
31)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 109° и OAB = 48°. Найдите угол BCO. Ответ дайте в градусах.
Ответ: 61
32)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 131° и OAB = 53°. Найдите угол BCO. Ответ дайте в градусах.
Ответ: 78
33)В угол C величиной 80° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Ответ: 100
34)В угол C величиной 73° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Ответ: 107
35)Касательные в точках A и B к окружности с центром O пересекаются под углом 60°. Найдите угол ABO. Ответ дайте в градусах.
Ответ: 30
36)Касательные в точках A и B к окружности с центром O пересекаются под углом 54°. Найдите угол ABO. Ответ дайте в градусах.
Ответ: 27
37)Хорды AC и BD окружности пересекаются в точке P, BP = 30, CP = 12, DP = 20 . Найдите AP.
Ответ: 50
38)Хорды AC и BD окружности пересекаются в точке P, BP = 4, CP = 12, DP = 24. Найдите AP.
Ответ: 6
39)На окружности отмечены точки A и B так, что меньшая дуга AB равна 142°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 71
40)На окружности отмечены точки A и B так, что меньшая дуга AB равна 96°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 48
41)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 12. Найдите AK.
Ответ: 6
42)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 27. Найдите AK.
Ответ: 9
43)Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 125°.
Ответ: 35
44)Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 135°.
Ответ: 45
45)Отрезок AB = 8 касается окружности радиуса 6 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Ответ: 4
46)Отрезок AB = 24 касается окружности радиуса 7 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Ответ: 18
47)К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 15, AO = 17.
Ответ: 8
48)К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8, AO = 10.
Ответ: 6
49)На отрезке AB выбрана точка C так, что AC = 7 и BC = 18. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Ответ: 24
50)На отрезке AB выбрана точка C так, что AC = 12 и BC = 8. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведѐнной из точки B к этой окружности.
Ответ: 16
51)Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 64°. Найдите величину угла OMK. Ответ дайте в градусах.
Ответ: 26
52)Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.
Ответ: 18
53)Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 9. Найдите диаметр окружности
Ответ: 30
54)Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 35. Найдите диаметр окружности.
Ответ: 74
55)Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 10.
Ответ: 20
56)Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 5.
Ответ: 2,5
57)Радиус круга равен 3. Найдите его площадь, деленную на π.
Ответ: 9
58)Радиус круга равен 5. Найдите его площадь, деленную на π.
Ответ: 25
59)Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 4 : 11. Найдите радиус окружности, если меньшая из сторон равна 16.
Ответ: 16
60)Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 7 : 8. Найдите радиус окружности, если меньшая из сторон равна 25.
Ответ: 25
61)В треугольнике ABC известно, что AC = 24, BC = 10, угол C равен 90°. Найдите радиус описанной окружности этого треугольника
Ответ: 13
62)В треугольнике ABC известно, что AC = 4, BC = 3, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
Ответ: 2,5
63)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите C, если A = 64°. Ответ дайте в градусах.
Ответ: 26
64)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите C, если A = 59°. Ответ дайте в градусах.
Ответ: 31
65)Радиус окружности с центром в точке O равен 65, длина хорды AB равна 126. Найдите расстояние от хорды AB до параллельной ей касательной k, если k и AB расположены по разные стороны от центра окружности.
Ответ: 81
66)Радиус окружности с центром в точке O равен 82, длина хорды AB равна 36. Найдите расстояние от хорды AB до параллельной ей касательной k, если k и AB расположены по разные стороны от центра окружности.
Ответ: 162
67)Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Ответ: 8
68)Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Ответ: 10
69)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.
Ответ: 3
70)Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠ABC = 107°. Найдите величину угла ВОС. Ответ дайте в градусах
Ответ: 73
71)Найдите площадь квадрата, описанного вокруг окружности радиуса 6.
Ответ: 144
72)Найдите площадь квадрата, описанного вокруг окружности радиуса 4.
Ответ: 64
Смотрите также на нашем сайте:
Задание 15 ОГЭ 2022 математика 9 класс с ответами
Прогрессии задание 14 ОГЭ 2022 математика 9 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
1. Задание 1 № 366577
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | сарай | баня | теплица |
| Цифры |
Прочитайте внимательно текст и выполните задание.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
2. Задание 2 № 366578
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Задание 3 № 366579
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
4. Задание 4 № 366581
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Задание 5 № 366582
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель | Прочее | Сред. расход | Стоимость газа / | |
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?
6. Задание 6 № 333006
Найдите значение выражения .
7. Задание 7 № 316336
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих неравенств верно?
1)
2)
3)
4)
8. Задание 8 № 401223
Сколько целых чисел расположено между и ?
9. Задание 9 № 333007
Решите уравнение .
10. Задание 10 № 325560
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
| Номер стрелка | Число выстрелов | Число попаданий |
| 1 | 42 | 28 |
| 2 | 70 | 20 |
| 3 | 54 | 45 |
| 4 | 46 | 42 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
11. Задание 11 № 34
Установите соответствие между графиками функций и формулами, которые их задают.
| А) | Б) | В) |
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А | Б | В |
12. Задание 12 № 311337
Длину окружности l можно вычислить по формуле , где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).
13. Задание 13 № 185
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
14. Задание 14 № 394427
Мощности пяти различных электромоторов составляют возрастающую геометрическую прогрессию. Мощность самого слабого электромотора — 5 кВт, а третьего по мощности — 20 кВт. Найдите мощность самого мощного электромотора, ответ дайте в кВт.
15. Задание 15 № 339495
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cosB.
16. Задание 16 № 356339
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
17. Задание 17 № 169878
Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
18. Задание 18 № 311958
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
19. Задание 19 № 340590
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
20. Задание 20 № 311588
Найдите значение выражения: при
21. Задание 21 № 338992
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
22. Задание 22 № 311576
Известно, что парабола проходит через точку и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
23. Задание 23 № 311548
Найдите величину угла AOE, если OE — биссектриса угла AOC, OD — биссектриса угла COB.
24. Задание 24 № 340387
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
25. Задание 25 № 339366
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 10 и MB = 18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.