Анализ геометрических высказываний
1. Задание 13 № 67. Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
2. Задание 13 № 93. Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
3. Задание 13 № 119. Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
4. Задание 13 № 145. Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
5. Задание 13 № 171. Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
6. Задание 13 № 197. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
7. Задание 13 № 169915. Какие из следующих утверждений верны?
1) Если угол равен 45°, то вертикальный с ним угол равен 45°.
2) Любые две прямые имеют ровно одну общую точку.
3) Через любые три точки проходит ровно одна прямая.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
8. Задание 13 № 169916. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
2) Любые две прямые имеют не менее одной общей точки.
3) Через любую точку проходит более одной прямой.
4) Любые три прямые имеют не менее одной общей точки.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
9. Задание 13 № 169917. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
10. Задание 13 № 169922. Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
11. Задание 13 № 169923. Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной окружности.
2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.
3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.
4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
12. Задание 13 № 169924. Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника равна 180°.
2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
3) Диагонали квадрата делят его углы пополам.
4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
13. Задание 13 № 169926. Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. Задание 13 № 169928. Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
15. Задание 13 № 169929. Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
16. Задание 13 № 169930. Какие из следующих утверждений верны?
1) Окружность имеет бесконечно много центров симметрии.
2) Прямая не имеет осей симметрии.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Квадрат не имеет центра симметрии.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
17. Задание 13 № 169931. Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей симметрии.
2) Прямая не имеет осей симметрии.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Равнобедренный треугольник имеет три оси симметрии.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
18. Задание 13 № 169932. Какие из следующих утверждений верны?
1) Центром симметрии прямоугольника является точка пересечения диагоналей.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
19. Задание 13 № 169933. Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
20. Задание 13 № 169934. Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
3) Стороны треугольника пропорциональны косинусам противолежащих углов.
4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
21. Задание 13 № 169935. Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
22. Задание 13 № 169936. Какие из следующих утверждений верны?
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
23. Задание 13 № 169938. Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
24. Задание 13 № 311684. Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
25. Задание 13 № 311763. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
26. Задание 13 № 311851. Укажите номера верных утверждений.
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
2) Через любые три точки проходит не более одной прямой.
3) Сумма вертикальных углов равна 180°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
27. Задание 13 № 311915. Укажите номера верных утверждений.
1) Площадь трапеции равна половине высоты, умноженной на разность оснований.
2) Через любые две точки можно провести прямую.
3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
28. Задание 13 № 311959. Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
29. Задание 13 № 314814. Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
30. Задание 13 № 314818. Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
31. Задание 13 № 314894. Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
32. Задание 13 № 316233. Укажите номера верных утверждений.
1) Смежные углы равны.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним равен 108°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
33. Задание 13 № 316286. Укажите номера верных утверждений.
1) Если угол равен 47°, то смежный с ним равен 153°.
2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Через любую точку проходит ровно одна прямая.
34. Задание 13 № 316323. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
35. Задание 13 № 316349. Укажите номера неверных утверждений.
1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
2) Диагонали ромба перпендикулярны.
3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
36. Задание 13 № 341332. Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
37. Задание 13 № 341358. Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2) В тупоугольном треугольнике все углы тупые.
3) Средняя линия трапеции равна полусумме её оснований.
38. Задание 13 № 341384. Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
39. Задание 13 № 341410. Какое из следующих утверждений верно?
1) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
40. Задание 13 № 341499. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
3) Все диаметры окружности равны между собой.
41. Задание 13 № 341525. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Сумма углов любого треугольника равна 360 градусам.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
42. Задание 13 № 341676. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
43. Задание 13 № 341710. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы равны.
В ответе запишите номер выбранного утверждения.
Новый октябрьский тренировочный вариант (тренировочная работа) №37812183 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812183:
На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы (сторона каждой клетки на плане равна 20 м). Въезд и выезд осуществляются через единственные ворота. При входе на территорию хозяйства слева от ворот находится кукурузное поле. Рядом с ним расположен яблоневый сад.
Также имеется цех по переработке овощей и фруктов, расположенный рядом с полем, засеянным капустой. При входе справа от ворот находится стоянка для грузовиков и сельхозтехники. На территории стоянки расположен склад готовой продукции. Участок с теплицами, в которых выращивают клубнику, граничит с яблоневым садом и капустным полем. К хозяйству подведено электричество.
Задание 1 № 368428 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Ответ: 2763
Задание 2 № 368429 Урожайность кукурузы в этом хозяйстве в среднем составила 4 тонны с одного гектара земли. Цех по переработке выпускает банки консервированной кукурузы массой нетто основного продукта 280 грамм каждая. Какое максимальное количество банок кукурузы выпустил цех?
Ответ: 17142
Задание 3 № 368430 Найдите суммарную площадь участков земли, занятых под сельскохозяйственные культуры. Ответ дайте в гектарах.
Ответ: 6,44
Задание 4 № 368431 По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).
Ответ: 440
Задание 5 № 368432 Собственник хозяйства рассматривает два варианта водоснабжения: централизованное или автономное из артезианской скважины. Цены на оборудование и стоимость его установки, данные о расходе воды и её стоимости даны в таблице. Обдумав оба варианта, собственник решил оборудовать автономное водоснабжение. Через сколько часов непрерывной работы водоснабжения экономия от использования автономного водоснабжения вместо централизованного компенсирует разность в стоимости установки оборудования и монтажа?
Ответ: 1600
Задание 10 № 132740 У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Ответ: 0,75
Задание 12 № 311528 Площадь треугольника можно вычислить по формуле , где — сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону , если площадь треугольника равна , а высота равна 14 м.
Ответ: 4
Задание 14 № 393958 Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
Ответ: 35000
Задание 15 № 323376 Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.
Ответ: 28
Задание 16 № 311331 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
Ответ: 71
Задание 17 № 169913 Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите площадь, деленную на π.
Ответ: 27
Задание 19 № 341384 Какие из следующих утверждений верны? 1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2) Средняя линия трапеции параллельна её основаниям. 3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Ответ: 23
Задание 21 № 314431 При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
Ответ: 2/1
Задание 24 № 340341 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Задание 25 № 78 Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Ответ: 0,6
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
-
Тренировочный вариант №22 ОГЭ 2022 по математике 9 класс с ответами
-
Пробный вариант №211004 ОГЭ 2022 по математике 9 класс 100 баллов с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
3,815
просмотров
Текст этой презентации
Слайд 1

Разбор и решение задания №9 ОГЭ по математике
Выполнила: ученица 9 класса Ж
Новикова Анастасия
Слайд 2

Цель работы:
Научиться решать задание №9 из ОГЭ модуля «Геометрия»
Подкорректировать усвоенные знания, умения и навыки.
Слайд 3

Так как задания №9 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей.
Слайд 4

Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Слайд 5

Медиана:
Слайд 6
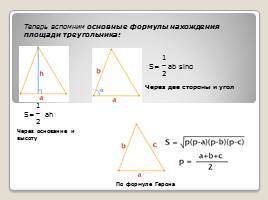
Теперь вспомним основные формулы нахождения площади треугольника:
1
2
ah
S=
S=
1
2
ab sinα
Через основание и высоту
Через две стороны и угол
По формуле Герона
Слайд 7
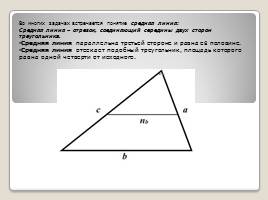
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия параллельна третьей стороне и равна её половине.
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Слайд 8
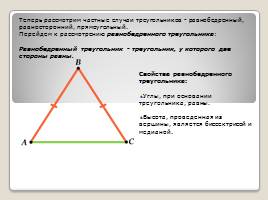
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника: Равнобедренный треугольник — треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника: Углы, при основании треугольника, равны. Высота, проведенная из вершины, является биссектрисой и медианой.
Слайд 9
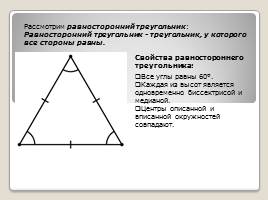
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
Все углы равны 60°.
Каждая из высот является одновременно биссектрисой и медианой.
Центры описанной и вписанной окружностей совпадают.
Свойства равностороннего треугольника:
Слайд 10

Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов прямой.
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Сумма острых углов треугольника равна 90:
Катет, лежащий против угла, равен половине гипотенузы.
Две высоты прямоугольного треугольника совпадают с его катетами.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Слайд 11
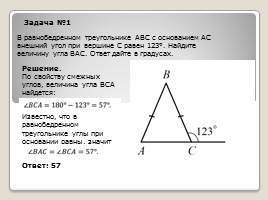
В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
Задача №1
Решение. По свойству смежных углов, величина угла ВСА найдется: Известно, что в равнобедренном треугольнике углы при основании равны, значит Ответ: 57
Слайд 12
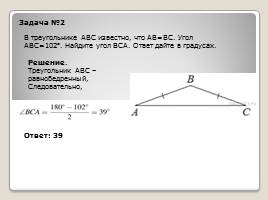
Задача №2
В треугольнике ABC известно, что АВ=ВС. Угол АВС=102. Найдите угол ВСА. Ответ дайте в градусах.
Решение.
Треугольник АВС – равнобедренный, Следовательно,
Ответ: 39
Слайд 13

Задача №3
В треугольнике ABC АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
Решение.
Треугольник АВС – равнобедренный, поэтому медиана, проведенная к основанию, является биссектрисой и высотой. Из прямоугольного треугольника АВМ по теореме Пифагора найдем ВМ:
Ответ: 9
Слайд 14

Задача №4
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет. Следовательно,
S = ½ • 15 • 4 = 30
Ответ:30
Слайд 15

Задача №5
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Решение
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18 Ответ: 18.
Прототипы заданий 16 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 16 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (окружность, круг и их элементы)
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 16 с ответамиИсточник: math100.ru → скачать |
| Прототипы задания 16 ОГЭ по математике (окружности) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 16 Автор: Е. А. Ширяева → теория → задания |
| Задания 16 — практика → Скачать вариант 1 → Скачать ответы 1 → Скачать вариант 2 → Скачать ответы 2 |
Решение типовых задач № 16 на ОГЭ по математике
Связанные страницы:
Задание 15 ОГЭ по математике — треугольники, четырёхугольники, многоугольники и их элементы
Задание 13 ОГЭ по математике — неравенства
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 14 ОГЭ по математике — задачи на прогрессии
Оценка 5
Подготовка к тестированию
Задание № 16 основного государственного экзамена модуль «Геометрия». В работе представлена презентация на тему :»Углы. смежные и вертикальные. Биссектриса угла». Задачи на вычисления углов. Подготовительная работа. Теория для повторения перед решением заданий 16 модуля «Геометрия». Задания можно дать для решения в 8 классе.
Скачать файл
Введите ваш emailВаш email
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 16 задания ОГЭ-2019 по математике.
14 ноября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 16
В равнобедренном треугольнике ABC с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
Решение
Треугольник АВС равнобедренный, поэтому угол ВАС равен углу ВСА. Но угол ВСА – смежный с углом в 123°. Следовательно
∠ВАС = ∠ВСА = 180° – 123° = 57°.
Ответ: 57°.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
| Задача №1
| Четырехугольник АВСD вписан в окружность. Угол АВС равен 38°, угол САD равен 33°. Найдите угол АВD. Ответ дайте в градусах. Дано: ∠АВС = 38°, ∠САD = 33°. Найти: ∠АВD. Решение: ∠DBC = ∠DAC = 38°, так как вписанные углы, опирающиеся на одну и ту же дугу DC. ∠АВD = ∠AВC — ∠DBC = 38° — 33° = 5° Ответ: 5. |
| Задача №2
| Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°. Дано: Sкруга = 69, угол кругового сектора равен 120°. Найти: Sсектора. Решение:
Ответ: 23. |
| Задача №3
| Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах. Дано: АВСD вписан в окружность, ∠А = 33°. Найти: ∠С. Решение: ∠C = 180° – ∠A = 180° – 33° = 147°, так как сумма противоположных углов вписанного четырехугольника равна 180°. Ответ: 147. |
| Задача №4
| Отрезки АС и BD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол АОD. Ответ дайте в градусах. Дано: АС и BD – диаметры окружности, ∠АСВ = 53°. Найти: ∠ АОD. Решение: 1)∠АCВ = 53° – вписанный угол, опирающийся на ᴗ АВ, поэтому ᴗ АВ = 53° 2 = 106°, так как вписанный угол измеряется половиной дуги, на которую он опирается. 2)BD – диаметр, значит ᴗ ВАD = 180°. 3) ∠ АОD – центральный угол, опирающийся на ᴗ АD, следовательно ∠ АОD = ᴗ АD = 180° – 106° = 74°. Ответ: 74. |
| Задача №5
| Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если АС = 9. Дано: АВ – d; r = 20,5; АС = 9. Найти: ВС. Решение: ∠C = 90°, так как угол, опирающийся на диаметр, r = 20,5, следовательно АВ = 20,5 2 = 41 По теореме Пифагора АВ2 = АС2 + ВС2 412 = 92 + ВС2 ВС2 = 1681 – 81 ВС2 = 1600 ВС = 40 Ответ: 40. |
| Задача №6
| Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах. Дано: ∠АВС = 61°, ∠ОАВ = 8°. Найти: ∠ ВСО. Решение: Проведем радиус ОВ, АО = ВО = СО = r. Треугольник АОВ – равнобедренный, значит ∠А = ∠АВО = 8°. Треугольник ВОС – равнобедренный, значит ∠ВСО = ∠ОВС= 61° – 8° = 53°. Ответ: 53. |
| Задача №7
| На окружности с центром О отмечены точки А и В так, что : ∠АОВ = 45°. Длина меньшей дуги равна 91. Найдите длину большей дуги. Дано: ∠АОВ = 45°, длина меньшей дуги равна 91. Найти: длину большей дуги. Решение:
Ответ: 637. |
| Задача №
| Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах. Дано: АВСD вписана в окружность, АD || ВС, ∠А = 77°. Найти: ∠С. Решение: ∠C = 180° – ∠A = 180° – 77° = 103°, так как сумма противоположных углов вписанного четырехугольника равна 180°. Ответ: 103. |
| Задача №9
| Четырехугольник АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найдите АD. Дано: АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найти: АD. Решение: АD + ВС = АВ + СD, так как суммы противоположных сторон описанного четырехугольника равны. АD + 12 = 8 + 13 АD = 21 – 12 АD = 9 Ответ: 9. |
| Задача №10
| Треугольник АВС вписан в окружность с центром О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°. Дано: треугольник АВС вписан в окружность, ∠АОВ = 73°. Найти: ∠АСВ. Решение: ∠ АОВ = 73° – центральный угол, опирающийся на ᴗ АВ, следовательно ᴗ АВ = 73°. ∠АСВ = 73° : 2 = 36, 5° , так как вписанный угол измеряется половиной дуги, на которую он опирается. Ответ: 36,5. |
| Задача №11
| Радиус окружности, вписанной в трапецию, равен 12. Найти высоту этой трапеции. Дано: трапеция вписана в окружность, r = 12. Найти: h. Решение: Высота трапеции равна диаметру вписанной окружности, поэтому h = 2 r = 2 12 = 24 . Ответ: 24. |
| Задача №12
| Сторона АВ треугольника АВС проходит через центр описанной около него окружности . Найдите ∠ А, если ∠В = 44°. Ответ дайте в градусах. Дано: треугольник АВС вписан в окружность, ∠В = 44 °. Найти: ∠А. Решение: ∠C = 90°, так как угол, опирающийся на диаметр, По теореме о сумме углов треугольника ∠А = 180° – (90° + 44°) = 46° Ответ: 46. |
| Задача №13
| Четырехугольник АВСD вписан в окружность. Угол АВD равен 37°, а угол САD равен 58°. Найдите угол АВС. Ответ дайте в градусах. Дано: АВСD вписан в окружность, ∠АВD = 37°, ∠САD = 58°. Найти: ∠АВС. Решение: Вписанный угол измеряется половиной дуги, на которую он опирается. ∠АВD = 37° – вписанный угол, опирающийся на ᴗ АD, поэтому ᴗ АD = 37° 2 = 74°. ∠САD = 58° – вписанный угол, опирающийся на ᴗ СD, поэтому ᴗ СD = 58° 2 = 116°. 3) ᴗ АDС = ᴗ АD + ᴗ DС = 74° + 116° = 190°, значит ∠АВС = 190° : 2 = 95°. Ответ: 95. |
| Задача №14
| Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠АВС = 107°. Найдите величину угла ВОС. Ответ дайте в градусах. Дано: АВС вписан в окружность, АВ = ВС, ∠АВС = 107°. Найти: ∠ВОС. Решение: Треугольник АВС равнобедренный, поэтому в нем углы при основании равны, то есть ∠А = ∠АСВ = (180° – 107°) : 2 = 36,5°. ∠ВАС = 36,5° – вписанный угол, опирающийся на ᴗ ВС, поэтому ᴗ ВС = 36,5° 2 = 73°. ∠ ВОС – центральный угол, опирающийся на ᴗ ВС, следовательно ∠ ВОС = ᴗ ВС = 73°. Ответ: 73. |
| Задача №15
| Радиус окружности, вписанной в равносторонний треугольник, равен 6. Найдите высоту этого треугольника. Дано: треугольник АВС описан около окружности, r = 6. Найти: h. Решение: В равностороннем треугольнике любая высота является медианой и биссектрисой и все они пересекаются в одной точке, которая является центром вписанной и описанной окружности. Медианы треугольника точкой пересечения делятся в отношении 2: 1, считая от вершины, значит h = 6 3 = 18. Ответ: 18. |
| Задача №16
| Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причем АВ = 2, АК = 4. Найдите АС. Дано: АК – касательная, АС – секущая, АВ = 2, АК = 4 Найти: АС. Решение: АК2 = АВ АС 42 = 2 АС АС = 16 : 2 АС = 8 Ответ: 8. |
| Задача №17
| Касательные в точках А и В к окружности с центром О пересекаются под углом 82°. Найдите угол АВО. Ответ дайте в градусах. Дано: касательные в точках А и В пересекаются под углом 82°. Найти: ∠АВО. Решение: Обозначим точку пересечения касательных буквой С . Отрезки касательных СА и СВ равны, значит треугольник АСВ равнобедренный, следовательно ∠САВ = ∠СВА = (180° – 82°) : 2 = 49°. Радиус окружности, проведенный в точку касания, перпендикулярен касательной, поэтому ∠АВС = 90°. ∠АВО = 90° – 49° = 41° Ответ: 41. |