{
Шестнадцатеричная система — 52e58.
Двоичная система — 1010010111001011000.
Посмотрите так же как пишутся десятичные цифры 83, 83, 94, 919, 23, 489, 955, 426, 2850, 8000, 4464, 75024, 63426, 989439, 617627 в различных системах счисления.
Число 339544 в других системах счисления:
2 — 1010010111001011000, 3 — 122020202201, 4 — 1102321120, 5 — 41331134, 6 — 11135544, 7 — 2612632, 8 — 1227130, 9 — 566681, 10 — 339544, 11 — 212117, 12 — 1445b4, 13 — bb71a, 14 — 8ba52, 15 — 6a914, 16 — 52e58, 17 — 411f3, 18 — 343ha, 19 — 2b9ae, 20 — 228h4, 21 — 1fdjg, 22 — 19jbi, 23 — 14kji, 24 — 10dbg, 25 — li6j, 26 — j87a, 27 — h6kj, 28 — fd2g, 29 — dqlc, 30 — ch84, 31 — bca1, 32 — abio.
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Объяснение:
решение во вложении
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
1)16*6=96
2)96:3=32
Пошаговое объяснение:
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
32 пакета.
Пошаговое объяснение:
В одном ящике 16кг,а в 6 таких ящиках
1) 6*16=96 кг моркови всего привезли.
В одном пакете 3кг.
2) 96:3=32 пакета с морковью.
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
5 минут
Объяснение:
Смотри фото
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Можно лучший ответ?)))
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Пусть 3 1/3 часа -3 часа 20 минут(200 минут) — первый насос
Пусть 1 1/2 раза — представим, как 1,5 раз — второй насос
3 часа 20 минут * 1,5 раза = 300 (мин)
300 — 200 = 100 (мин) или 1 ч. 40 мин.- откачают воду оба насоса
ответ: за 1 ч. 40 мин.
Обвести кружком
номер правильного ответа:
-
Больной ,находящийся
в сопоре :
-
на вопросы отвечает
и реагирует на уколы -
на вопросы не
отвечает, на уколы реагирует -
на вопросы не
отвечает, на уколы не реагирует
Установить
соответствие:
2. Патология
Вынужденное положение
1. Менингит
А. ортопноэ
2. Сердечная
недостаточность Б. С приведенными к
животу
ногами
3. Гидроторакс
В. Лягавой собаки
4. Острый живот
Г. На больном боку
.Д.
Молящегося муллы
Ответ : 1…, 2…, 3…,
4… .
Обвести кружком
номера всех правильных ответов:
3.Акроцианозом
называется синюшность:
-
губ
-
лица
-
мочек ушей
-
кончика носа
-
шеи и верхней
части грудной клетки -
ногтей
Дополнить:
4.У больного
,находящегося в лежачем положении, отеки
появляются сначала в области _____________.
5.Видимое на глаз
увеличение щитовидной железы называется
________.
Эталоны ответов
№ 15
15.1. 3.
15.2. 1 В , 2 А , 3 Г , 4 Б
.
15.3. 1,3,4,6.
15.4. крестца
15.5. зоб.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обозначим АВС. АС-основание. Проведем высоту с вершины В. Пункт пересечения обозначим Н. Значит АН=26/2=13 см, так как высота в равнобедренном треугольнике является медианой и биссектрисой. Треугольник АВН-прямоугольный. Угол АВН=60 градусов. Значит угол ВАН=30 градусов, с этого получается, что ВН в два раза меньше, чем АВ, потому что лежит против угла в 30 градусов. Пусть ВН-х см, тогда АВ=2х см. По теореме Пифагора 4х²=х²+169, 3х²=169, х=√169/3 =13/√3. S=1/2*26*13/√3=(169√3)/3 см².
В четырёх маленьких клетках 3*4=12 кроликов.
В пяти больших клетках 9*5=45 кроликов .
вроде так
Ответ:
Купили -8 рулонов обоев.
Длиной по 10м 50 см.
Израсходовали 3/4 части.
Ск. метров обоев осталось-?
10 м 50 см = 1050 см
1) 8*1050=8400 (см) или 84 (м) — обоев всего
2) 8400*3/4=252/4 (см) или 63 (м) — израсходовали
3) 84 — 63 = 21 (м) — осталось
ответ: 21 м обоев остался
Пошаговое объяснение:
км/ч — скорость вертолета
км/ч — скорость самолета
км — пролетел самолет за 5 часов
ОТВЕТ: 2175 км
Условие
15 номер задания
математика 10-11 класс
396
Все решения
Написать комментарий
lmevengore850
Вопрос по русскому языку:
Помогите пожалуйста задание номер 15
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
perve
Что именно помочь?
Это легко!
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Русский язык.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Русский язык — один из восточнославянских языков, национальный язык русского народа.
- ОГЭ по математике
Проверочная работа по геометрии. 4 варианта по 8 заданий с ответами. Многоугольники (параллелограмм, прямоугольник)
→ скачать pdf
→ скачать docx
Пример заданий:
Диагонали AC и BD параллелограмма ABCD пересекаются в точке О, АС=10, BD=22, AB=9. Найдите DO.
Связанные страницы:
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.
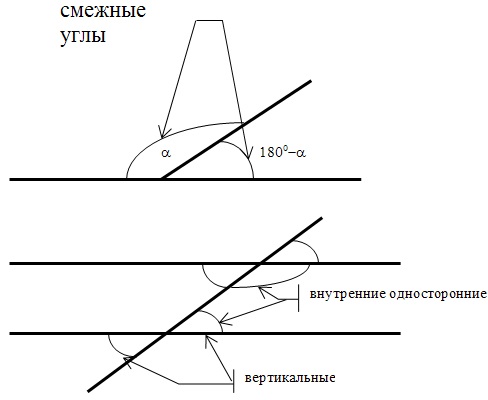
Вначале предлагаю рассмотреть углы на плоскости:
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
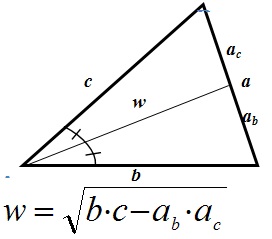 Медиана:
Медиана:
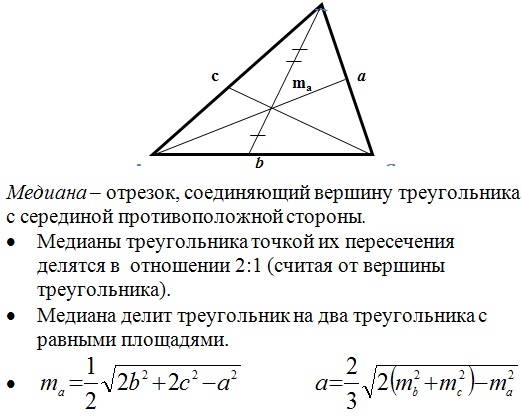
Теперь вспомним основные формулы нахождения площади треугольника:
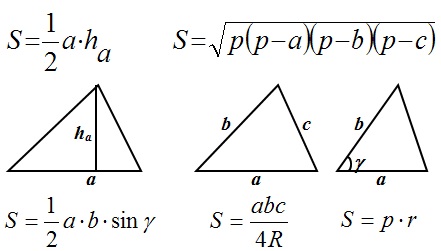
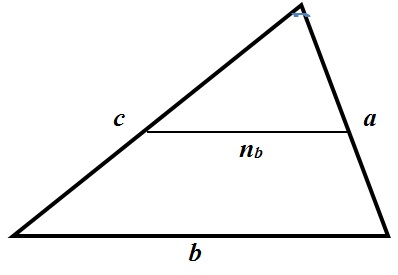
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник – треугольник, у которого две стороны равны.
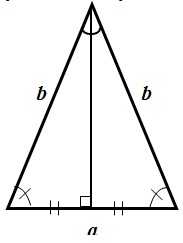
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник – треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
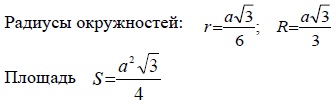 Прямоугольный треугольник:
Прямоугольный треугольник:

В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Для решения этого задания достаточно знать правило – сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 – 73 – 48 = 59
Ответ: 59
pазбирался: Даниил Романович | обсудить разбор | оценить
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия – это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC – третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Если в треугольнике две стороны равны – значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 – 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m – медиана в равностороннем треугольнике, а a – сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
pазбирался: Даниил Романович | обсудить разбор | оценить
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 – 23 = 67°
Ответ: 67
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Для решения необходимо вспомнить определение медианы.
Медиана – отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28
pазбирался: Даниил Романович | обсудить разбор | оценить
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор | оценить
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
pазбирался: Даниил Романович | обсудить разбор | оценить
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 – 123 = 57°
Из второго – что ∠BCA = ∠BAC = 57°
Ответ: 57
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор | оценить
Каталог заданий.
Действия с обыкновенными дробями
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 6 № 314127
Найдите значение выражения
Аналоги к заданию № 311234: 314127 32 311235 314128 314173 314175 314176 314177 314184 314186 … Все
Источник: Банк заданий ФИПИ
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 6 № 314264
Вычислите:
Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все
Источник: Банк заданий ФИПИ
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 6 № 314265
Вычислите:
Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все
Источник: Банк заданий ФИПИ
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 6 № 314288
Найдите значение выражения
Аналоги к заданию № 314282: 314288 333111 314283 314284 314285 314286 314287 314289 314290 314291 … Все
Источник: Банк заданий ФИПИ
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 6 № 333006
Найдите значение выражения .
Аналоги к заданию № 333006: 337375 353450 Все
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О категории
Неравенства и системы неравенств.
Практика (8)
Укажите неравенство, решение которого изображено на рисунке.
1)x^2+64>0
2)x^2-64>0
3)x^2-64<0
4)x^2+64<0
Решите систему неравенств
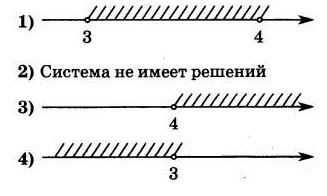
[m]left{ begin{array}{c} x > 3 4-x < 0 end{array} right.[/m]
На каком рисунке изображено множество её решений?
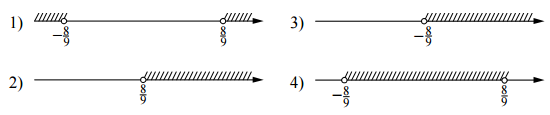
Укажите множество решений неравенства 81x^2>64
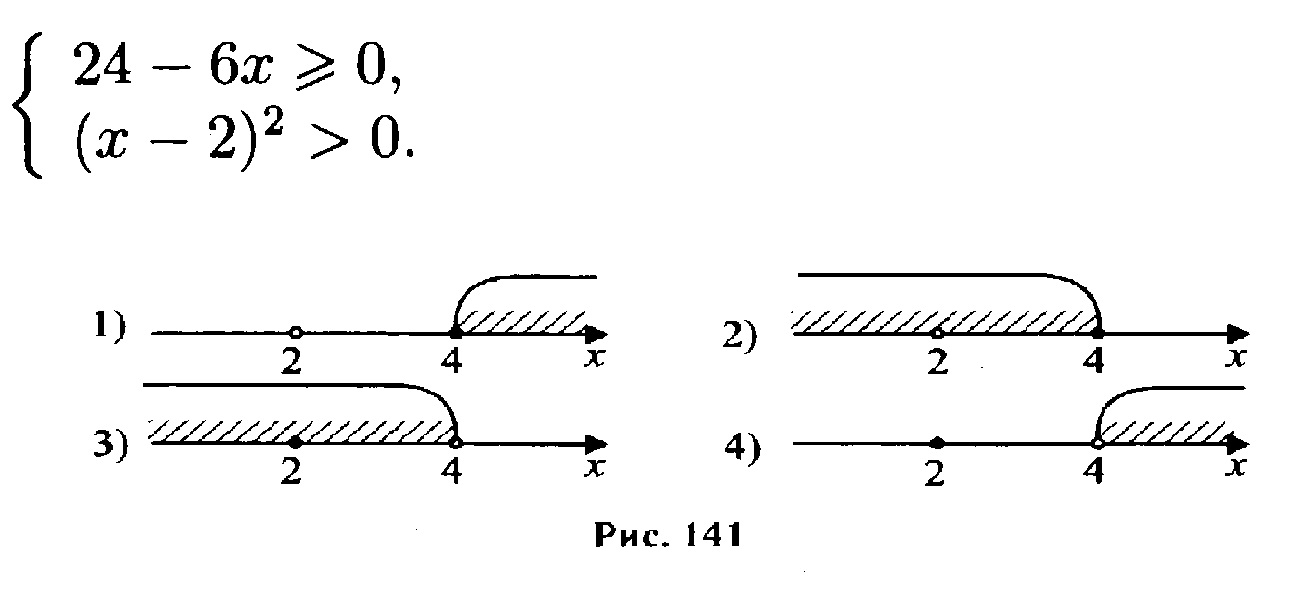
Решите систему неравенств. В ответе укажите номер координатной прямой (см. рис. 141), на которой изображено множество её решений.
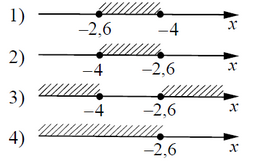
Решить систему неравенств [m]left{ begin{array}{c} x+2,6 ≤ 0 x+5 ≥ 1 end{array} right.[/m]
На каком рисунке изображено множество ее решений?
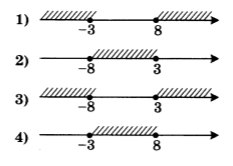
Решите неравенство (x+3)(x-8) ≥ 0
На каком рисунке изображено множество его решений?
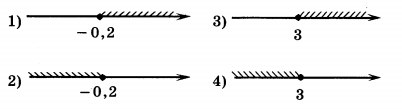
Укажите множество решений неравенства x+4 ≥ 4x-5.
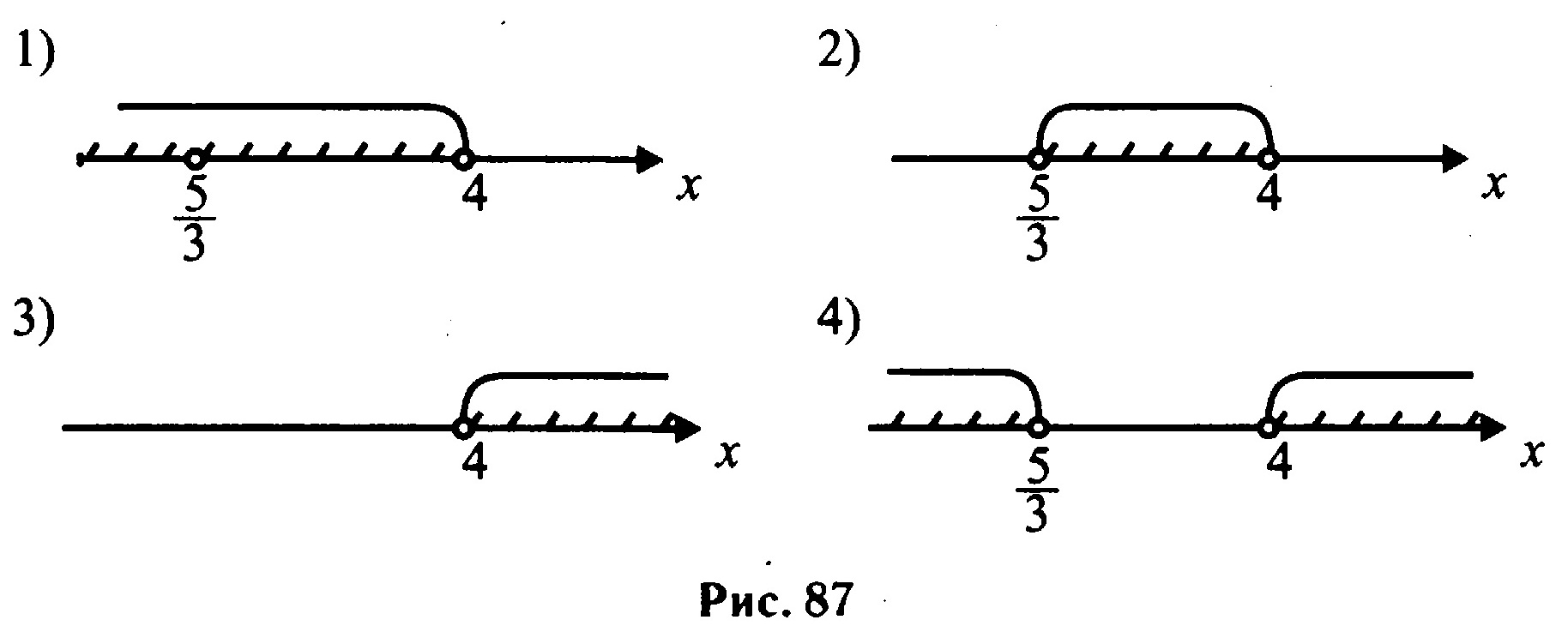
На какой из координатных прямых (см. рис. 87) изображено множество решений системы неравенств [m]left{ begin{array}{c} 3x-5>0 15-4x<-1 end{array} right.[/m]
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 15 задания ОГЭ-2019 по математике.
14 ноября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
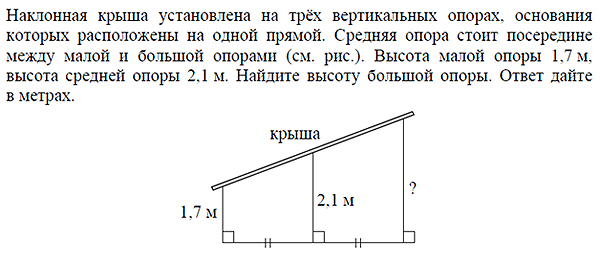
Задание 15
Решение
Фигура, изображенная на рисунке, является прямоугольной трапецией. Средняя опора есть не что иное, как средняя линия трапеции, длина которой вычисляется по формуле
где a, b – длины оснований. Составим уравнение:
b = 2,5.
Ответ: 2,5.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Простой способ вычислить проценты от X
Сколько будет %
от ?
15% от 339544 это: 50931.6
Процент от — Таблица для 339544
| Процент от | Разница |
|---|---|
| 1% от 339544 это 3395.44 | 336148.56 |
| 2% от 339544 это 6790.88 | 332753.12 |
| 3% от 339544 это 10186.32 | 329357.68 |
| 4% от 339544 это 13581.76 | 325962.24 |
| 5% от 339544 это 16977.2 | 322566.8 |
| 6% от 339544 это 20372.64 | 319171.36 |
| 7% от 339544 это 23768.08 | 315775.92 |
| 8% от 339544 это 27163.52 | 312380.48 |
| 9% от 339544 это 30558.96 | 308985.04 |
| 10% от 339544 это 33954.4 | 305589.6 |
| 11% от 339544 это 37349.84 | 302194.16 |
| 12% от 339544 это 40745.28 | 298798.72 |
| 13% от 339544 это 44140.72 | 295403.28 |
| 14% от 339544 это 47536.16 | 292007.84 |
| 15% от 339544 это 50931.6 | 288612.4 |
| 16% от 339544 это 54327.04 | 285216.96 |
| 17% от 339544 это 57722.48 | 281821.52 |
| 18% от 339544 это 61117.92 | 278426.08 |
| 19% от 339544 это 64513.36 | 275030.64 |
| 20% от 339544 это 67908.8 | 271635.2 |
| 21% от 339544 это 71304.24 | 268239.76 |
| 22% от 339544 это 74699.68 | 264844.32 |
| 23% от 339544 это 78095.12 | 261448.88 |
| 24% от 339544 это 81490.56 | 258053.44 |
| 25% от 339544 это 84886 | 254658 |
| 26% от 339544 это 88281.44 | 251262.56 |
| 27% от 339544 это 91676.88 | 247867.12 |
| 28% от 339544 это 95072.32 | 244471.68 |
| 29% от 339544 это 98467.76 | 241076.24 |
| 30% от 339544 это 101863.2 | 237680.8 |
| 31% от 339544 это 105258.64 | 234285.36 |
| 32% от 339544 это 108654.08 | 230889.92 |
| 33% от 339544 это 112049.52 | 227494.48 |
| 34% от 339544 это 115444.96 | 224099.04 |
| 35% от 339544 это 118840.4 | 220703.6 |
| 36% от 339544 это 122235.84 | 217308.16 |
| 37% от 339544 это 125631.28 | 213912.72 |
| 38% от 339544 это 129026.72 | 210517.28 |
| 39% от 339544 это 132422.16 | 207121.84 |
| 40% от 339544 это 135817.6 | 203726.4 |
| 41% от 339544 это 139213.04 | 200330.96 |
| 42% от 339544 это 142608.48 | 196935.52 |
| 43% от 339544 это 146003.92 | 193540.08 |
| 44% от 339544 это 149399.36 | 190144.64 |
| 45% от 339544 это 152794.8 | 186749.2 |
| 46% от 339544 это 156190.24 | 183353.76 |
| 47% от 339544 это 159585.68 | 179958.32 |
| 48% от 339544 это 162981.12 | 176562.88 |
| 49% от 339544 это 166376.56 | 173167.44 |
| 50% от 339544 это 169772 | 169772 |
| 51% от 339544 это 173167.44 | 166376.56 |
| 52% от 339544 это 176562.88 | 162981.12 |
| 53% от 339544 это 179958.32 | 159585.68 |
| 54% от 339544 это 183353.76 | 156190.24 |
| 55% от 339544 это 186749.2 | 152794.8 |
| 56% от 339544 это 190144.64 | 149399.36 |
| 57% от 339544 это 193540.08 | 146003.92 |
| 58% от 339544 это 196935.52 | 142608.48 |
| 59% от 339544 это 200330.96 | 139213.04 |
| 60% от 339544 это 203726.4 | 135817.6 |
| 61% от 339544 это 207121.84 | 132422.16 |
| 62% от 339544 это 210517.28 | 129026.72 |
| 63% от 339544 это 213912.72 | 125631.28 |
| 64% от 339544 это 217308.16 | 122235.84 |
| 65% от 339544 это 220703.6 | 118840.4 |
| 66% от 339544 это 224099.04 | 115444.96 |
| 67% от 339544 это 227494.48 | 112049.52 |
| 68% от 339544 это 230889.92 | 108654.08 |
| 69% от 339544 это 234285.36 | 105258.64 |
| 70% от 339544 это 237680.8 | 101863.2 |
| 71% от 339544 это 241076.24 | 98467.76 |
| 72% от 339544 это 244471.68 | 95072.32 |
| 73% от 339544 это 247867.12 | 91676.88 |
| 74% от 339544 это 251262.56 | 88281.44 |
| 75% от 339544 это 254658 | 84886 |
| 76% от 339544 это 258053.44 | 81490.56 |
| 77% от 339544 это 261448.88 | 78095.12 |
| 78% от 339544 это 264844.32 | 74699.68 |
| 79% от 339544 это 268239.76 | 71304.24 |
| 80% от 339544 это 271635.2 | 67908.8 |
| 81% от 339544 это 275030.64 | 64513.36 |
| 82% от 339544 это 278426.08 | 61117.92 |
| 83% от 339544 это 281821.52 | 57722.48 |
| 84% от 339544 это 285216.96 | 54327.04 |
| 85% от 339544 это 288612.4 | 50931.6 |
| 86% от 339544 это 292007.84 | 47536.16 |
| 87% от 339544 это 295403.28 | 44140.72 |
| 88% от 339544 это 298798.72 | 40745.28 |
| 89% от 339544 это 302194.16 | 37349.84 |
| 90% от 339544 это 305589.6 | 33954.4 |
| 91% от 339544 это 308985.04 | 30558.96 |
| 92% от 339544 это 312380.48 | 27163.52 |
| 93% от 339544 это 315775.92 | 23768.08 |
| 94% от 339544 это 319171.36 | 20372.64 |
| 95% от 339544 это 322566.8 | 16977.2 |
| 96% от 339544 это 325962.24 | 13581.76 |
| 97% от 339544 это 329357.68 | 10186.32 |
| 98% от 339544 это 332753.12 | 6790.88 |
| 99% от 339544 это 336148.56 | 3395.44 |
| 100% от 339544 это 339544 | 0 |
Как можно рассчитать 15% от 339544
В магазине товар стоит 339544₽, вам дали скидку 15% и вы хотите понять сколько вы сэкономили.
Решение:
Сэкономленная сумма = Цена товара * Скидка в процентах/ 100
Сэкономленная сумма = (15 * 339544) / 100
Сэкономленная сумма = 50931.6₽
Проще говоря, при покупке товара за 339544₽ и скидке в 15%, вы заплатите 288612.4₽ и при этом сэкономите 50931.6₽.
Для рассчета НДС от 339544₽, вы можете использовать Калькулятор НДС онлайн
Расчеты процентов: примеры
- 30 от 2000
- 30 от 1000
- 30 от 300
- 30 от 5000
- 56% от 273746
- 4% от 203629
- 94% от 294363
- 66% от 272598
- 20% от 203756
- 45% от 14073
- 86% от 286548
- 53% от 233
- 47% от 214203
- 27% от 361065
- 8% от 94063
- 1% от 60632
- 20 от 40
- 20 от 4000
- 40 от 200
- 12 от 40000
percent-calc.com © 2023