- ОГЭ по математике
Как решать задание 12 ОГЭ по математике? Материал для подготовки к ОГЭ.
Для выполнения задания 12 необходимо уметь осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами.
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.
Решение типовых задач № 12 на ОГЭ по математике
| Карточки для отработки задания 12 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 12 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 12 (презентация) Автор: Духина Марина Васильевна → скачать |
| Презентация: Решение заданий 12 ОГЭ математикаАвтор: Малявина Алена Сергеевна → скачать |
Связанные страницы:
Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №12. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Выразим сопротивление R:
R = P / I2
Подставим значения в полученную формулу:
R = 224 / 42 = 224 / 16 = 14 ом
Ответ: 14
pазбирался: Даниил Романович | обсудить разбор | оценить
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:
С = 6000 + 4100•n,
где n — число колец, установленных в колодце.
Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную формулу значение n = 7:
С = 6000 + 4100•7 = 6000 + 28700 = 34700
Ответ: 34700
pазбирался: Даниил Романович | обсудить разбор | оценить
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:
T = 2 • √l
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Выразим из формулы l, для этого возведем обе части в квадрат, получим:
T ² = 4 • l ,
тогда:
l = T ² / 4
Подставляя значения из условия, получаем:
l = 3 ² / 4 = 9 / 4 = 2,25
Ответ: 2,25
pазбирался: Даниил Романович | обсудить разбор | оценить
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой
tF = 1,8 • tC + 32,
где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?
Подставляем значение -25 в формулу:
tF = 1,8 • (-25) + 32 = -45 + 32 = -13
Ответ: -13
pазбирался: Даниил Романович | обсудить разбор | оценить
Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде
где F — сила взаимодействия в ньютонах, q1 и q2 — величины зарядов в кулонах, k — коэффициент пропорциональности в Н·м2/Кл2, а r — расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9·109 Н·м2/Кл2, q2=0,004 Кл, r=600 м, F=0,4 Н.
Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q1, а справа – все остальные величины, фигурирующие в начальной формуле.
Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:
Далее r2 из знаменателя слева переносим в числитель справа, а k и q2 из числителя слева – в знаменатель справа. Получим:
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).
Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:
Ответ: 0,004
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырёхугольника можно вычислить по формуле:
![]()
где d1 и d2 – длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1=13, sinα=3/13, а S=25,5.
Так как искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:
![]()
В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:
 Ответ: 17
Ответ: 17
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1 и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8=d1×16×252
В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251
Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
1 слайд
Урок алгебры в 9 классе Автор разработки: учитель математики МБОУ СШ №10 г. Павлово Леонтьева Светлана Ивановна Ни одна наука так не укрепляет веру в силу человеческого разума, как математика. Гуго Штейнгауз Урок опубликован на сайте: http://pavls1954.wixsite.com/1712
2 слайд
Приветствую вас на уроке алгебры Уроки №104-105 26.04.18г. Успехов в усвоении учебного материала Учитесь так, словно вы постоянно ощущаете нехватку своих знаний. Конфуций
3 слайд
1.Теория. Повторить материал по теме «Прогрессии» 2.Практика. ДР№50 на 26.04.18 Задания ОГЭ № 13 Проанализировать задания №11 (на прогрессии)
4 слайд
Карточка ответов в работе №2 от 26.04.2018 Карточка ответов в работе №1 от 26.04.2018___________________________ вариант ___ _ № вопроса1234567891011121314Оценка Ответ Баллы
5 слайд
Классная работа Подготовка к ОГЭ. Задания №12 26.04.18
6 слайд
Закрепить умение выполнять задания типа 12. Развивать умение анализировать, сравнивать, обобщать. Продолжить формирование культуры устной и письменной речи, умения оценивать уровень своих знаний. Цели урока:
7 слайд
1. Найти значение выражения при Ваш вариант решения Вариант 1 Задание №12
8 слайд
1. Найти значение выражения при
9 слайд
1. Найти значение выражения при
10 слайд
1.2 Найти значение выражения при Выполните самостоятельно, сверьте ответы Вариант 4 Задание №12
11 слайд
3 Найти значение выражения при Вариант 6 Задание №12 Предложите вариант решения
12 слайд
3 Найти значение выражения при Вариант 6 Задание №12
13 слайд
3 Найти значение выражения при Вариант 6 Задание №12
14 слайд
3 Найти значение выражения при Вариант 6 Задание №12
15 слайд
3 Найти значение выражения при Вариант 6 Задание №12
16 слайд
3 Найти значение выражения при Вариант 6 Задание №12
17 слайд
3 Найти значение выражения при Вариант 6 Задание №12
18 слайд
3 Найти значение выражения при Вариант 6 Задание №12
19 слайд
4 Найти значение выражения при Вариант 11 Задание №12 Прокомментируйте шаги решения, назовите НОЗ и дополнительные множители к слагаемым
20 слайд
4 Найти значение выражения при Вариант 11 Задание №12 Назовите слагаемые числителя
21 слайд
4 Найти значение выражения при Вариант 11 Задание №12
22 слайд
4 Найти значение выражения при Вариант 11 Задание №12
23 слайд
5 Найти значение выражения при Вариант 15 Задание №12 Прокомментируйте шаги решения, назовите НОЗ и дополнительные множители к слагаемым
24 слайд
5 Найти значение выражения при Вариант 15 Задание №12 Упростите выражение
25 слайд
5 Найти значение выражения при Вариант 15 Задание №12
26 слайд
5 Найти значение выражения при Вариант 15 Задание №12
27 слайд
5 Найти значение выражения при Вариант 15 Задание №12
28 слайд
6 Найти значение выражения при Вариант 19 Задание №12 Нужно ли дроби приводить к НОЗ? Что нужно сделать?
29 слайд
6 Найти значение выражения при Вариант 19 Задание №12
30 слайд
6 Найти значение выражения при Вариант 19 Задание №12
31 слайд
6 Найти значение выражения при Вариант 22 Задание №12
32 слайд
7 Найти значение выражения при Вариант 26 Задание №12 Укажите порядок преобразований
33 слайд
7 Найти значение выражения при Вариант 26 Задание №12
34 слайд
7 Найти значение выражения при Вариант 26 Задание №12
35 слайд
7 Найти значение выражения при Вариант 26 Задание №12
36 слайд
7 Найти значение выражения при Вариант 26 Задание №12
37 слайд
7 Найти значение выражения при Вариант 26 Задание №12
38 слайд
8 Найти значение выражения при Вариант 37 Задание №12
39 слайд
8 Найти значение выражения при Вариант 37 Задание №12
40 слайд
8 Найти значение выражения при Вариант 37 Задание №12
41 слайд
8 Найти значение выражения при Вариант 37 Задание №12
42 слайд
8 Найти значение выражения при Вариант 37 Задание №12
43 слайд
9 Найти значение выражения при Вариант 39 Задание №12 Что нужно сделать?
44 слайд
9 Найти значение выражения при Вариант 39 Задание №12
45 слайд
9 Найти значение выражения при Вариант 39 Задание №12
46 слайд
9 Найти значение выражения при Вариант 39 Задание №12
47 слайд
9 Найти значение выражения при Вариант 39 Задание №12
48 слайд
10 Найти значение выражения при Вариант 46 Задание №12
49 слайд
10 Найти значение выражения при Вариант 46 Задание №12
50 слайд
10 Найти значение выражения при Вариант 46 Задание №12
51 слайд
10 Найти значение выражения при Вариант 46 Задание №12
52 слайд
10 Найти значение выражения при Вариант 46 Задание №12
53 слайд
10 Найти значение выражения при Вариант 46 Задание №12
54 слайд
11. Решите неравенство и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта. Вариант 1 Задание №12
55 слайд
11. Решите неравенство и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
57 слайд
Какие задания выполняли на уроке? Подводим итоги урока
58 слайд
Проведите рефлексию — Материал урока был понятен и усвоен хорошо. — Были небольшие трудности. — Проявились ранние пробелы в знаниях, не все было понятно, нужно обратиться за консультацией к учителю или однокласснику. Оцените понимание материала. Поставьте средний балл.
59 слайд
1.Теория. Повторить материал по решению теме «Системы уравнений» 2.Практика. ДР№51 на 26.04.18 Задания ОГЭ № 12 Проанализировать задания 1-14 №11 (на прогрессии)- прорешать по типам заданий
Задание 12 № 338296
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
О категории
Числовые последовательности, арифметические, геометрические прогрессии
Практика (12)
Дана арифметическая прогрессия (a_(n)), в которой a_9=-22,2, a_(23)=-41,8. Найдите разность прогрессии.
Арифметическая прогрессия (а_(n)) задана условиями:
a_(1) = -9, a_(n+1) = a_(n)+4
Найдите сумму первых шести её членов.
Дана арифметическая прогрессия (а_(n)): -7; -5; -3; … . Найдите a_(16).
Дана арифметическая прогрессия (a_(n)), разность которой равна − 8,5, a_(1)=− 6,8. Найдите a_(11).
Последовательность (C_(n)) задана условиями C1=5, C_(n+1) = C_(n) − 4.
Найдите c6.
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Выписаны первые несколько членов геометрической прогрессии: − 1024; − 256; − 64; … Найдите сумму первых пяти её членов.
Даны 12 чисел. Первое число равно 25, а каждое следующее меньше предыдущего на 3. Найдите двенадцатое число из данных чисел.
Даны 7 чисел. Первое число равно 15, а каждое следующее на 3 меньше предыдущего. Найдите седьмое число из данных чисел.
Дана арифметическая прогрессия 6, 2, -2, … . Найдите сумму семи её членов, начиная с четвертого и заканчивая десятым.
Выписаны первые несколько членов геометрической прогрессии:
-158;-79;-39,5;….
Найдите её четвёртый член.
Дана арифметическая прогрессия -5, 2, 9, … . Найдите сумму шести её членов, начиная с четвертого и заканчивая десятым.
meavis957
Вопрос по алгебре:
Помогите, пожалуйста, номер 12
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
ustercagrama65
У=13х-13tgx-18
При к=0
х=0 ∈[0; π/4]
Этот х не входит в промежуток [0; π/4]
При х=0 у=13*0-13tg0-18= -18 — наибольшее
При х=π/4 у=
Ответ: -18
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
ответы по начерталке в I-EXAM.docx
Скачиваний:
269
Добавлен:
11.05.2015
Размер:
1.69 Mб
Скачать
-
Крепежные
детали, у которых на чертеже диаметр
стержней равны 2
мм и менее, изображают условно. -
В
стандартных крепежных резьбовых деталях
используется метрическая
резьба. -
К
деталям, которые крепятся к объекту
или сцепляются друг с другом при помощи
резьбового соединения относятся болт
и гайка -
Рабочая
длина болта- это длина болта
без головки -
Штампованное
или точеное кольцо, которое подкладывается
под гайку или головку бота называется
шайбой -
На
чертеже изображен болт

-
На
чертеже изображена крепежная деталь,
называемая
гайкой -
Правильное
изображение шлица на головке винта на
виде слева показано на рисунке

-
При
упрощенном изображении шлицы на головках
винтов изображают утолщенной
линией.
Задание №13
-
Деталь,
устанавливаемая в пазах соединяемых
деталей для предотвращения их
относительного перемещения при передаче
крутящего момента, называется шпонкой -
В
комплект шпоночного соединения входят:
вал, втулка,
шпонка -
Для
ограничения осевого перемещения деталей
применяют шплинты -
Изображенная
деталь называется

-
Деталь,
передающая движение от вала к втулке
и наоборот, называется шпилькой -
На
рисунке изображено соединение
клиновидной
шпонкой.
-
Условное
обозначение «Шпонка 12 х 8 х 60» означает,
что призматическая шпонка имеет
следующие размеры. Ширина-12мм,
высота-8мм, длинна-60мм -
Положение
прорезных и корончатых гаек фиксируется
посредством шплинта -
К
зубчатым соединениям относятся шлицевые
Задание №14
-
Соединения,
при разборке которых разрушаются
детали, их состовляющие, называются
неразъемными -
Неразъемные
соединения, основанные на использовании
сил молекулярного сцепления и получаемые
путем местного нагрева деталей до
расплавленного состояния, называются
сварным -
Вспомогательный
знак, для обозначения швов сварных
соединений «Усиление шва снять»
изображен на рисунке

-
При
обозначении сварного шва знак «Наплывы
и неровности шва обработать с плавны
переходом к основному металлу», изображен
на рисунке.. -
При
обозначении сварного шва соединения
трубы и фланца применяется
угловое расположение
деталей. -
При
наличии на чертеже нескольких одинаковых
сварных швов наносят обозначение одного
шва -
Клеевой
шов, как паяный, изображается на чертеже
сплошной линией толщиной 2S -
Соединение
сварное
не
является
разъемным. -
Соединение,
в котором отсутствует расплавление
или высокотемпературный нагрев
соединяемых деталей называется паяным
Вопрос №15
-
Данные
для обработки отверстий под установочные
винты, заклепки, штифты, производимые
при сборке изделий, помещают на
сборочном чертеже. -
Качество
поверхностей детали, точность размеров
формы, их допустимая шероховатость
задаются на чертеже условными
графическими знаками. -
На
детали, полученные сваркой,
допускается не
выполнять
чертежи. -
На
изделие, полученное разрезкой заготовки
на части, применяемые совместно,
разрабатывается один
чертеж. -
На
чертежах деталей применяют условные
обозначения (знаки, линии и
т.п.),установленные в государственных
стандартах без
указания номера стандарта. -
На
чертежах деталей, в которых в готовом
изделии центровые отверстия недопустимы,
указывают знак
К. -
На
чертежах деталей, выполняемых из
изделий-заготовок, элементы
изделия-заготовки, которые не подлежат
дополнительной обработке, изображают
линиями сплошными
тонкими -
Необходимость
придерживаться стандартизованных
величин при назначении линейных и
угловых размеров на чертеже позволяет
унифицировать
режущий и измерительный инструменты -
Оси
для цилиндрических деталей, обрабатываемых
на токарном станке, располагают
горизонтально.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подставим у:
наибольшее значение 4, при х = 0, у = -4
Ответ: 4
Опубликовано — 2 года назад | По предмету
Математика |
автор Аккаунт удален
Самые новые вопросы
Литература — 1 минута назад
Как повёл себя директор, когда узнал,что лидия михайловна играет в замеряшки. уроки французкого в.распутин
Литература — 3 минуты назад
О чем рассуждает раскольников перед совершением преступления? за что он осуждает себя? какое оправдание он ищет своему
Литература — 5 минут назад
Какой урок вынес для себя наш герой?из повести конь с розовой гривой в.п. астафьев
Литература — 7 минут назад
Мое впечатление о повести алые паруса
Литература — 9 минут назад
Какие из этих произведений могли бы войти в сборник «юмористические рассказы»? прыжок толстой что любит мишка драгунский
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:
Значит, им понадобится
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.
Площадь заказника равна:
Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения:
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:
Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из приведенных утверждений неверно?
1)
2)
3)
4)
Решение.
Заметим, что и Проверим все варианты ответа:
1) — неверно;
2) — верно;
3) — верно;
4) — верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения
1)
2)
3)
4)
Решение.
Последовательно получим:
Ответ: 1
9. Задание 9 № 338500
При каком значении значения выражений и равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение Решим его:
Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.
1) функция возрастает на промежутке
2)
3)
4) прямая пересекает график в точках и
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .
2) — неверно,
3) — верно, видно из графика.
4) Прямая пересекает график в точках и — верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .
Решение.
Выразим :
Подставляя, получаем:
Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:
Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:
Ответ: 377 мест.
15. Задание 15 № 340000
В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите
Решение.
Из прямоугольного треугольника по теореме Пифагора найдём
Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
Ответ: 0,2.
16. Задание 16 № 351463
На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842
Найдите угол
Решение.
Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение
Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ
Ответ:
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:
График функции сводится к графику параболы с выколотой точкой
Выделим полный квадрат:
Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)
Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и
Ответ: 16.
24. Задание 24 № 155
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.
По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,
Площадь трапеции :
Площадь трапеции
Ответ: 9.
Огэ по математике 338296
Задание 12 № 338296
Закон Менделеева-Клапейрона можно записать в виде PV = ΝRT, где P — давление (в паскалях), V — объём (в м 3 ), Ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если Ν = 68,2 моль, P = 37 782,8 Па, V = 6 м 3 .
Выразим температуру из закона Клапейрона-Менделеева: Подставляя, получаем:
Задание 12 № 338296
Задание 12 338296.
Oge. sdamgia. ru
09.12.2018 2:49:59
2018-12-09 02:49:59
Источники:
Https://oge. sdamgia. ru/problem? id=338296
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ по математике 338296
Огэ по математике 338296
Огэ по математике 338296
Задание 12 № 338394
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м 3 ), Ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 400 К, P = 13 296 Па, V = 4,9 м 3 .
Задание 12 № 338394
Закон Менделеева Клапейрона можно записать в виде PV νRT, где P давление в паскалях, V объём в м 3 , ν количество вещества в молях, T температура в градусах Кельвина, а R универсальная газовая постоянная, равная 8,31 Дж К моль.
Reshuoge. ru
16.09.2019 13:47:12
2019-09-16 13:47:12
Источники:
Https://reshuoge. ru/problem? id=338394
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ по математике 338296
Огэ по математике 338296
Огэ по математике 338296
Задание 12 № 311824
Чтобы перевести значение температуры по шкале Цельсия (T °C) в шкалу Фаренгейта (T °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Подставим в формулу значение переменной F:
Задание 12 № 311964
Из закона всемирного тяготения выразите массу M и найдите её величину (в килограммах), если и гравитационная постоянная
Выразим массу: Подставим значения переменных:
Задание 12 № 338296
Закон Менделеева-Клапейрона можно записать в виде PV = ΝRT, где P — давление (в паскалях), V — объём (в м 3 ), Ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если Ν = 68,2 моль, P = 37 782,8 Па, V = 6 м 3 .
Выразим температуру из закона Клапейрона-Менделеева: Подставляя, получаем:
Задание 12 № 338296
Задание 12 № 311964
Закон Менделеева-Клапейрона можно записать в виде PV νRT, где P давление в паскалях, V объём в м 3 , ν количество вещества в молях, T температура в градусах Кельвина, а R универсальная газовая постоянная, равная 8,31 Дж К моль.
Oge. sdamgia. ru
24.06.2020 0:44:24
2020-06-24 00:44:24
Источники:
Https://oge. sdamgia. ru/test? theme=27&sort=hard
В 12-ом задании мы сталкиваемся с прогрессиями — общими понятиями. Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые. Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.
Ответом в задании 12 является целое число или конечная десятичная дробь.
Теория к заданию №12
Начнем теоретическую справку об определениях прогрессий.
Арифметическая прогрессия:
Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.
an+1 = an + d
где d – разность прогрессии
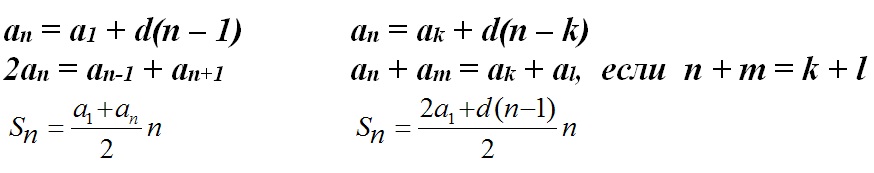
Геометрическая прогрессия:
Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.
bn+1 = bn q
где q – знаменатель прогрессии
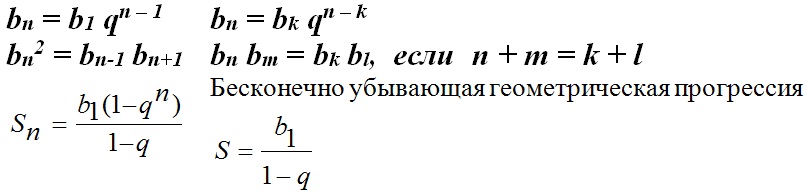
В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.
Разбор типовых вариантов задания №12 ОГЭ по математике.
Первый вариант задания (нахождение разности прогрессии)
Дана арифметическая прогрессия a(n) в которой
a (3) = 6,9
a (16) = 26,4
Найдите разность прогрессии.
Решение:
Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).
Находим разницу между значениями a (3) и a (16):
a (3) — a (16) = 26,4 — 6,9 = 19,5
Находим количество членов:
16 — 3 = 13
Находим разность прогрессии:
19,5 / 13 = 1,5
Ответ: 1,5
Второй вариант задания (нахождение неизвестного члена)
Выписано несколько последовательных членов геометрической прогрессии:
-1, x, -49, -343, ….
Найдите x.
Решение:
Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:
-343 / -49 = 7
Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.
x = -49 / 7 = -7
Ответ: -7
Третий вариант задания (нахождение n-ого члена)
Выписаны первые несколько членов арифметической прогрессии: 10, 6, 2, …
Найдите 101 член.
Решение:
Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:
an = a1 + (n-1) • d
В нашем случае:
a1 = 10
d = 6 — 10 = -4
Подставляем значения в формулу:
a101 = 10 + (101-1) • (-4) = -390
Ответ: -390
Демонстрационный вариант ОГЭ 2019
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение:
В данном задании нас проверяют на знание формулы арифметической прогрессии:
![]()
где n — номер члена прогрессии, d — разность, а а1 — первый член.
Решение:
Подставим в общую формулу известные из условия значения:
d = 4,
а1 = 6,
n = 15,
получим:
a15 = 6 + (15 — 1) • 4
вычислив, получаем значение 15 члена:
a15 = 62
Ответ: 62
Четвертый вариант задания (нахождение произвольного члена геометрической прогрессии)
Геометрическая прогрессия (bn) задана условиями:
b1=–2, bn+1=2bn.
Найдите b7.
Решение:
Искомый 7-й член прогрессии b7 будем искать по формуле:
b7=b1·q6. (1)
Здесь b1 по условию дано, а знаменатель q нет. Но его можно определить, исходя из определения этой величины. Согласно определению, q=bn+1/bn. Используя второе условие задачи, получим, что q=2.
Теперь используем 1-е условие задачи (b1=–2) и найдем искомую величину по формуле (1):
b7=–2·26=–2·64=–128.
Ответ: –128
Пятый вариант задания (нахождение суммы n членов геометрической прогрессии)
Выписаны первые три члена геометрической прогрессии: 1512; –252; 42; … Найдите сумму первых четырёх ее членов.
Решение:
Сумму произвольного кол-ва членов геометрич.прогрессии будем искать по формуле:
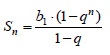
1-й член прогрессии известен из условия и равен b1=1512. Требуемое число членов n=4.
Знаменатель прогрессии найдем как частное двух соседних членов прогрессии (2-го и 1-го или 3-го и 2-го и т.д.). Найдем его так:
![]()
По условию b2=–252, b3=42, поэтому
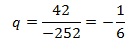
Отсюда получаем:
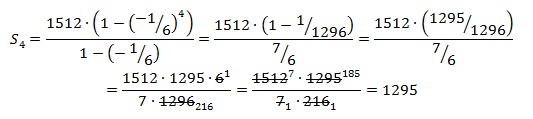
Ответ: 1295
Задание № 12.
Конституция РФ. Выбор позиций из списка.
Как выполнить задание № 12. РЕКОМЕНДАЦИИ.
Комментарий задания.
Задание № 1 включает в себя вопросы по теме: «Конституция РФ». Необходимо из списка выбрать положения Конституции РФ по определённым вопросам.
Алгоритм выполнения.
1.Внимательно прочитайте задание.
2.Из вопроса выделите главное – о каком конкретно положении Конституции идёт речь.
3.Внимательно вдумывайтесь в каждое предложение предполагаемого ответа.
4.Запишите ответ цифрами, ещё раз проверив его.
Общая рекомендация:
постоянно читайте статьи Конституции, запоминайте основные её положения; номера статей учить не нужно, это не требуется на ЕГЭ.
Разберём конкретный пример.
12.Что из перечисленного ниже относится к конституционным гарантиям местного самоуправления в Российской Федерации? Запишите цифры, под которыми они указаны.
1) право вносить проекты федеральных законов
2) право на судебную защиту
3) право на самоопределение
4) неподотчётность органам государственной власти
5) запрет на ограничение прав местного самоуправления
Пояснение.
Сначала чётко определяем, какова суть вопроса: обязанности органов местного самоуправления.
Разберём каждое высказывание.
1) право вносить проекты федеральных законов — нет, неверно, не имеют такого права.
Вспомним, кто имеет право вносит законодательную инициативу:
2) право на судебную защиту — да, верно.
Положение Конституции: «Местное самоуправление в Российской Федерации гарантируется правом на судебную защиту» (статья 133)
3) право на самоопределение — нет, неверно, не имеют такого права.
Самоопределение – это право самостоятельно определять круг полномочий, не являться частью публичной власти в стране. Местное самоуправление имеет право на самостоятельность деятельности, но только в рамках закона и чётко ограниченных Конституцией полномочий.
Не путайте понятия самостоятельность и самоопределение!
4) неподотчётность органам государственной власти — нет, неверно, не имеют такого права.
Органы местного самоуправления подотчётны органам государственной власти, обязаны действовать в соответствии с Конституцией РФ,
5) запрет на ограничение прав местного самоуправления — да, верно.
Положение Конституции:
«Местное самоуправление в Российской Федерации гарантируется на компенсацию дополнительных расходов, возникших в результате выполнения органами местного самоуправления во взаимодействии с органами государственной власти публичных функций, а также запретом на ограничение прав местного самоуправления, установленных Конституцией Российской Федерации и федеральными законами». (Статья 133).
Ответ: 25.
Вернутьсяк списку тестов по обществознанию ЕГЭ

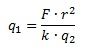
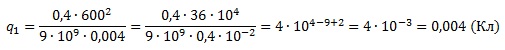 Ответ: 0,004
Ответ: 0,004

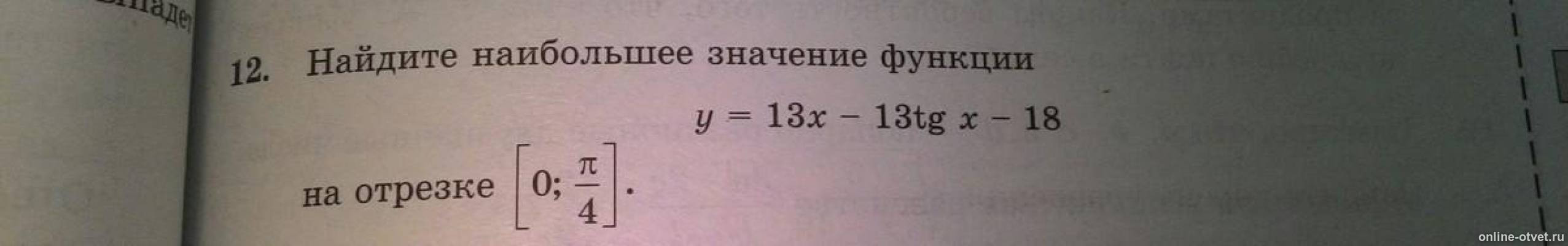









 пачек чая.
пачек чая.

 км.
км. руб.
руб.






 и
и  Проверим все варианты ответа:
Проверим все варианты ответа:






 значения выражений
значения выражений  и
и  равны?
равны? Решим его:
Решим его:

 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.



 пересекает график в точках
пересекает график в точках  и
и 
 и затем возрастает на
и затем возрастает на  .
. — неверно,
— неверно, 

 — верно, видно из графика.
— верно, видно из графика. пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика. , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
. :
:







 катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
 по теореме Пифагора найдём
по теореме Пифагора найдём 

 и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги. равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
 .
.


 часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 






 г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%. И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку. равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:
 с выколотой точкой
с выколотой точкой 

 сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)
 имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 


 следовательно, треугольники
следовательно, треугольники  равны. Так как
равны. Так как  =
=  треугольники
треугольники  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
 :
: 




