- ОГЭ по математике
Как решать задание 12 ОГЭ по математике? Материал для подготовки к ОГЭ.
Для выполнения задания 12 необходимо уметь осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами.
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.
Решение типовых задач № 12 на ОГЭ по математике
| Карточки для отработки задания 12 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 12 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 12 (презентация) Автор: Духина Марина Васильевна → скачать |
| Презентация: Решение заданий 12 ОГЭ математикаАвтор: Малявина Алена Сергеевна → скачать |
Связанные страницы:
Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №12. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Выразим сопротивление R:
R = P / I2
Подставим значения в полученную формулу:
R = 224 / 42 = 224 / 16 = 14 ом
Ответ: 14
pазбирался: Даниил Романович | обсудить разбор | оценить
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:
С = 6000 + 4100•n,
где n — число колец, установленных в колодце.
Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную формулу значение n = 7:
С = 6000 + 4100•7 = 6000 + 28700 = 34700
Ответ: 34700
pазбирался: Даниил Романович | обсудить разбор | оценить
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:
T = 2 • √l
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Выразим из формулы l, для этого возведем обе части в квадрат, получим:
T ² = 4 • l ,
тогда:
l = T ² / 4
Подставляя значения из условия, получаем:
l = 3 ² / 4 = 9 / 4 = 2,25
Ответ: 2,25
pазбирался: Даниил Романович | обсудить разбор | оценить
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой
tF = 1,8 • tC + 32,
где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?
Подставляем значение -25 в формулу:
tF = 1,8 • (-25) + 32 = -45 + 32 = -13
Ответ: -13
pазбирался: Даниил Романович | обсудить разбор | оценить
Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде
где F — сила взаимодействия в ньютонах, q1 и q2 — величины зарядов в кулонах, k — коэффициент пропорциональности в Н·м2/Кл2, а r — расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9·109 Н·м2/Кл2, q2=0,004 Кл, r=600 м, F=0,4 Н.
Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q1, а справа – все остальные величины, фигурирующие в начальной формуле.
Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:
Далее r2 из знаменателя слева переносим в числитель справа, а k и q2 из числителя слева – в знаменатель справа. Получим:
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).
Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:
Ответ: 0,004
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырёхугольника можно вычислить по формуле:
где d1 и d2 – длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1=13, sinα=3/13, а S=25,5.
Так как искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:
![]()
В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:
 Ответ: 17
Ответ: 17
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1 и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8=d1×16×252
В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251
Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 12 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 12
Решение
Вместо того чтобы сразу подставить числа в данное выражение, сначала упростим его, записав в виде рациональной дроби:
Ответ: 1,25.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Заец Мирослав Владимирович
учитель математики школы №1317 г. Москвы
Хотите сохранить материал на будущее? Отправьте себе на почту
{
Шестнадцатеричная система — 52888.
Двоичная система — 1010010100010001000.
Посмотрите так же как пишутся десятичные цифры 78, 4, 81, 814, 698, 545, 14, 43, 5459, 4572, 7271, 77279, 8088, 86363, 951434 в различных системах счисления.
Число 338056 в других системах счисления:
2 — 1010010100010001000, 3 — 122011201121, 4 — 1102202020, 5 — 41304211, 6 — 11125024, 7 — 2605405, 8 — 1224210, 9 — 564647, 10 — 338056, 11 — 210a94, 12 — 143774, 13 — bab44, 14 — 8b2ac, 15 — 6a271, 16 — 52888, 17 — 40dcb, 18 — 33h6g, 19 — 2b588, 20 — 2252g, 21 — 1fabj, 22 — 19ga4, 23 — 14i12, 24 — 10alg, 25 — lfm6, 26 — j624, 27 — h4jg, 28 — fb5c, 29 — dos3, 30 — cfig, 31 — bao1, 32 — aa48.
Число 338056 (триста тридцать восемь тысяч пятьдесят шесть) — шестизначное четное, делится на два, сорок две тысячи двести пятьдесят семь и само себя.
Т.е число 338056 делится на 2, 42257, 338056, и раскладывается на множители: 2:2:2:42257.
Проверка:
338056 : 2 = 169028
169028 : 2 = 84514
84514 : 2 = 42257
42257 : 42257 = 1
Сумма цифр в числе 338056 равна 25, а их умножение (отличных от нуля) — 2160.
Обратное число 338056 = 2.9580897839411E-6
Двоичная система счисления 3380562: 1010010100010001000
Проверка:
| 262144 | +262144 (218) | 1 |
| 131072 | 0 | |
| 65536 | +65536 (216) | 1 |
| 32768 | 0 | |
| 16384 | 0 | |
| 8192 | +8192 (213) | 1 |
| 4096 | 0 | |
| 2048 | +2048 (211) | 1 |
| 1024 | 0 | |
| 512 | 0 | |
| 256 | 0 | |
| 128 | +128 (27) | 1 |
| 64 | 0 | |
| 32 | 0 | |
| 16 | 0 | |
| 8 | +8 (23) | 1 |
| 4 | 0 | |
| 2 | 0 | |
| 1 | 0 |
Примеры:
338056 + 3447879 = 3785935
триста тридцать восемь тысяч пятьдесят шесть плюс три миллиона четыреста сорок семь тысяч восемьсот семьдесят девять равно три миллиона семьсот восемьдесят пять тысяч девятьсот тридцать пять
8378866 + 338056 = 8716922
восемь миллионов триста семьдесят восемь тысяч восемьсот шестьдесят шесть плюс триста тридцать восемь тысяч пятьдесят шесть равно восемь миллионов семьсот шестнадцать тысяч девятьсот двадцать два
494229 — 338056 = 156173
четыреста девяносто четыре тысячи двести двадцать девять минус триста тридцать восемь тысяч пятьдесят шесть равно сто пятьдесят шесть тысяч сто семьдесят три
338056 — 2785555 = -2447499
триста тридцать восемь тысяч пятьдесят шесть минус два миллиона семьсот восемьдесят пять тысяч пятьсот пятьдесят пять равно минус два миллиона четыреста сорок семь тысяч четыреста девяносто девять
Предыдущее число: 338055 (триста тридцать восемь тысяч пятьдесят пять), а следующее число — 338057 (триста тридцать восемь тысяч пятьдесят семь).
Вы ждали 0.01сек.
триста тридцать восемь тысяч пятьдесят шесть
На этой странице мы собрали информацию о том, как пишется число 338056 прописью.
Число 338056 правильно пишется — триста тридцать восемь тысяч пятьдесят шесть
С помощью нашего сервиса, Вы сможете узнать как пишется любое число словами. Просто введите число в форму и получите результат.
Посмотрите как пишутся другие чифры прописью 59, 55, 58, 71, 292, 406, 940, 624, 787, 3661, 4604
Свойства числа 338056
| Множители | 2 * 2 * 2 * 42257 | |
| Делители | 1, 2, 4, 8, 42257, 84514, 169028, 338056 | |
| Количество делителей | 8 | |
| Сумма делителей | 633870 | |
| Предыдущее целое | 338055 | |
| Следующее целое | 338057 | |
| Простое число? | NO | |
| Предыдущее простое | 338033 | |
| Следующее простое | 338119 | |
| 338056th простое число | 4839941 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1010010100010001000 | |
| Восьмеричная | 1224210 | |
| Двенадцатеричный | 143774 | |
| Шестнадцатиричная | 52888 | |
| Квадрат | 114281859136 | |
| Квадратный корень | 581.42583361939 | |
| Натуральный логарифм | 12.730966841215 | |
| Десятичный логарифм | 5.528988648433 | |
| Синус | 0.97800558173116 | |
| Косинус | -0.208578719199 | |
| Тангенс | -4.6889039566786 |
Математические настройки для вашего сайта
Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2022
numberempire.com
Все права защищены
Опубликовано — 2 года назад | По предмету
Математика |
автор Аккаунт удален
Самые новые вопросы
Литература — 1 минута назад
Как повёл себя директор, когда узнал,что лидия михайловна играет в замеряшки. уроки французкого в.распутин
Литература — 3 минуты назад
О чем рассуждает раскольников перед совершением преступления? за что он осуждает себя? какое оправдание он ищет своему
Литература — 5 минут назад
Какой урок вынес для себя наш герой?из повести конь с розовой гривой в.п. астафьев
Литература — 7 минут назад
Мое впечатление о повести алые паруса
Литература — 9 минут назад
Какие из этих произведений могли бы войти в сборник «юмористические рассказы»? прыжок толстой что любит мишка драгунский
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Задание 14. Вычисление по формуле
1. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах ![]() . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
. Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
Решение.
Подставим в формулу значение переменной :
![]()
Ответ: 183.
Ответ: 183
202
183
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1303.
2. Площадь параллелограмма ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и
— стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и ![]() .
.
Решение.
Подставим в формулу известные значения величин: ![]()
Ответ: 60.
Ответ: 60
311326
60
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)
3. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле ![]() , где
, где ![]() — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
— число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
Решение.
Подставим количество колец в формулу для расчета стоимости. Имеем:
![]()
Ответ: 50 500.
Ответ: 50500
311533
50500
Источник: ГИА-2013. Математика. Экзамен. Вариант 17
4. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
Решение.
Найдём какое расстояние прошёл человек, подставим длину шага и число шагов в формулу:
![]()
Ответ: 1,28
Ответ: 1,28
338071
1,28
5. Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение.
Найдем расстояние, на котором находится наблюдатель от места удара молнии:
![]()
Ответ: 3.
Ответ: 3
338396
3
6. Из формулы центростремительного ускорения a = ω2R найдите R (в метрах), если ω = 4 с−1 и a = 64 м/с2.
Разные задачи
1. Период колебания математического маятника ![]() (в секундах) приближенно можно вычислить по формуле
(в секундах) приближенно можно вычислить по формуле ![]() , где
, где ![]() — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
— длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение.
Подставим в формулу значение ![]() :
: ![]()
Ответ: 2,25.
Ответ: 2,25
46
2,25
Источник: Демонстрационная версия ГИА—2013 по математике.
2. Радиус описанной около треугольника окружности можно найти по формуле ![]() , где
, где ![]() — сторона треугольника,
— сторона треугольника, ![]() — противолежащий этой стороне угол, а
— противолежащий этой стороне угол, а ![]() — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите
— радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите ![]() , если , а .
, если , а .
Решение.
Выразим из формулы ![]() :
:
Подставляя, получаем:
Ответ: 0,4.
Ответ: 0,4
311534
0,4
Источник: ГИА-2013. Математика. Московская обл. Пробные варианты(1 вар)
3. Длину биссектрисы треугольника, проведённой к стороне ![]() , можно вычислить по формуле . Вычислите , если .
, можно вычислить по формуле . Вычислите , если .
Решение.
Выразим из данной формулы :
Подставляя, получаем:
Ответ: 0,8.
Ответ: 0,8
311536
0,8
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
4. За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за t минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Линейные уравнения
1. Длину окружности ![]() можно вычислить по формуле , где
можно вычислить по формуле , где ![]() — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать
— радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).
Решение.
Выразим радиус из формулы длины окружности:
Подставляя, получаем:
Ответ: 13.
Ответ: 13
311337
13
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)
2. Площадь ромба ![]() можно вычислить по формуле , где
можно вычислить по формуле , где — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ
, если диагональ
равна 30 м, а площадь ромба 120 м2.
Решение.
Подставим в формулу известные величины:
Ответ: 8.
Ответ: 8
311348
8
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 3)
3. Площадь треугольника ![]() можно вычислить по формуле , где
можно вычислить по формуле , где ![]() — сторона треугольника,
— сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
, если площадь треугольника равна , а высота
равна 14 м.
Решение.
Выразим сторону ![]() из формулы площади треугольника:
из формулы площади треугольника:
Подставляя, получаем:
Ответ: 4.
Ответ: 4
311528
4
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
4. Площадь трапеции ![]() можно вычислить по формуле , где
можно вычислить по формуле , где ![]() — основания трапеции,
— основания трапеции, — высота (в метрах). Пользуясь этой формулой, найдите высоту
, если основания трапеции равны
и
, а её площадь .
Решение.
Выразим высоту трапеции из формулы площади:
Подставляя, получаем:
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
311530
4
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
5. Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле , где ![]() и
и — катеты, а
— гипотенуза треугольника. Пользуясь этой формулой, найдите
, если и
.
Решение.
Подставим в формулу известные значения величин:
Ответ: 3,2.
Ответ: 3,2
311535
3,2
Источник: ГИА-2013. Математика. Московская обл. Пробные варианты(2 вар)
6. Объём пирамиды вычисляют по формуле , где — площадь основания пирамиды,
— её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Решение.
Выразим высоту пирамиды из формулы для ее объема:
Подставляя, получаем:
Ответ: 8.
Ответ: 8
311541
8
Источник: ГИА-2013. Математика. Тренировочная работа № 3. (1 вар)
7. Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а
![]() угол между ними. Вычислите
угол между ними. Вычислите ![]() , если .
, если .
Решение.
Выразим ![]() :
:
Подставляя, получаем:
Ответ: 0,4.
Ответ: 0,4
311543
0,4
Источник: ГИА-2012. Математика. Диагностическая работа № 1(2 вар)
8. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Решение.
Подставим в формулу значение переменной :
Ответ: −14,4.
Ответ: -14,4
311824
-14,4
9. Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле где — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
Решение.
Выразим радиус окружности: Подставим значения переменных ![]() и
и
Ответ: 5.
Ответ: 5
311920
5
10. Из закона всемирного тяготения выразите массу и найдите её величину (в килограммах), если
и гравитационная постоянная
Решение.
Выразим массу: Подставим значения переменных:
Ответ: 1000.
Ответ: 1000
311964
1000
11. Полную механическую энергию тела (в джоулях) можно вычислить по формуле где — масса тела (в килограммах),
— его скорость (в м/с),
— высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а
— ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите
(в метрах), если а
Решение.
Выразим высоту: Подставим значения переменных:
Ответ: 5.
Ответ: 5
316355
5
12. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.
Решение.
Выразим сопротивление из формулы для мощности:
Подставляя, получаем:
Ответ: 6.
Ответ: 6
316914
6
13. Закон Кулона можно записать в виде где — сила взаимодействия зарядов (в ньютонах),
и
— величины зарядов (в кулонах),
— коэффициент пропорциональности (в Н·м2/Кл2 ), а
— расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда
(в кулонах), если Н·м2/Кл2, Кл, м, а Н.
Решение.
Выразим заряд из закона Кулона:
Подставляя, получаем:
Ответ: 0,004.
Ответ: 0,004
318530
0,004
14. Закон всемирного тяготения можно записать в виде где — сила притяжения между телами (в ньютонах),
и
— массы тел (в килограммах),
— расстояние между центрами масс (в метрах), а
— гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела
(в килограммах), если Н, кг, а
м.
Решение.
Выразим заряд из закона всемирного тяготения:
Подставляя, получаем:
Ответ: 4000.
Ответ: 4000
338056
4000
15. Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187 Дж, I = 9 A, R = 3 Ом.
Решение.
Выразим время из формулы Джоуля-Ленца: Подставляя, находим:
Ответ: 9.
Ответ: 9
338089
9
16. Площадь четырёхугольника можно вычислить по формуле где и
— длины диагоналей четырёхугольника,
![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали если
a
Решение.
Выразим длину диагонали из формулы для площади четырёхугольника:
Подставляя, получаем:
Ответ: 4.
Ответ: 4
338238
4
17. Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.

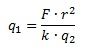
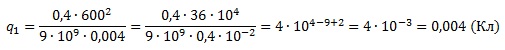 Ответ: 0,004
Ответ: 0,004