1)
Постройте аналогичную модель
для
сетевого
графика, приведенного на листе з12
Вашего
рабочего файла.
2) Убедитесь в
правильности ее функционирования,
задавая различные варианты исходных
данных. Основные результаты рекомендуется
нанести непосредственно на график.
11. Вычисление обратной матрицы
Известно,
что при расчете межотраслевого баланса
потребуется, как и в ряде других расчетов,
вычислять обратную матрицу. В Excel есть
функция МОБР,
единственным
аргументом которой является блок ячеек,
содержащих исходную матрицу. В приведенном
примере такому блоку присвоено имя
Исходная_матрица.
Но эта функция возвращает результат в
виде массива, размещенного в одной
ячейке. Поэтому, чтобы сформировать
обратную матрицу, необходимо использовать
один из приведенных ниже способов.
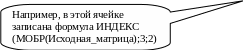
Первый
способ основан на использовании функции
ИНДЕКС,
которая в списке функций находится
в категории
Ссылки и
массивы.
В
качестве аргументов этой функции надо
указать функцию МОБР
вместе с ее аргументом, а также индексы
строки и столбца. Пример выполнения
таких вычислений приведен ниже (рис.
11.1). Можно рекомендовать следующий
порядок ввода этих формул. Сначала
вызвать функцию ИНДЕКС,
выбирая первый из возможных списков
аргументов (первым аргументом в этом
списке будет массив). При запросе на
ввод массива щелкните по любой пустой
ячейке, а в поля для номеров строки и
столбца введите по единице. В результате
получится ноль, но достаточно в записанном
выражении выделить временно введенную
пустую ячейку и вызвать функцию МОБР,
указав в качестве ее аргумента исходную
матрицу, чтобы получить элемент обратной
матрицы с заданными индексами. Копируем
эту ячейку в остальные ячейки столбца,
исправляем индексы, затем заполняем
остальные элементы матрицы.
Для
матрицы большей размерности такое
исправление индексов становится
трудоемким и можно применить второй
вариант выполнения вычислений. Если
ввести в соответствующие ячейки величины
индексов для строк и столбцов, то в
выражении для элемента a*11
обратной матрицы на позиции для индексов
надо указать ссылки на ячейки с единичными
значениями индексов. Сделаем абсолютными
адрес столбца для ячейки с индексом
строки и адрес строки для ячейки с
индексом столбца. Тогда при копировании
вычисленного элемента получим все
элементы обратной матрицы без
редактирования индексов.
Чтобы
убедиться в правильности вычислений,
присвоим ячейкам с полученным результатом
имя Обратная_матрица
и перемножим эти матрицы, используя
функцию МУМНОЖ
(рис. 11.1).
Должна получиться единичная матрица.
Так как все вычисления реализуются с
ограниченной точностью, то возможно
появление вместо нулей малых по абсолютной
величине значений.
Исходная матрица
Обратная матрица
Индексы
1 2 3
1
1
2 3 -2,167 0,8333 0,3333
2
3
4 5 1,8333 -0,167 -0,667
3
2 3
7 -0,167 -0,167 0,3333
Единичная матрица
1
0 0 -2,167 0,8333 0,3333
0
1 0 1,8333 -0,167 -0,667
0
0 1 -0,167 -0,167 0,3333
Рис. 11.1. Вычисление
обратной матрицы
Второй
способ основан на использовании формулы
массива, которая может выполнить
требуемые вычисления, а затем вернуть
всю группу значений. Для этого необходимо
предварительно выделить диапазон ячеек,
которые будут содержать результаты
вычислений, потом ввести формулу, но
вместо того, чтобы нажимать клавишу
ENTER
или щелкать по кнопке OK
в диалоговом окне мастера функций,
следует нажать клавиши
CTRL+SHIFT+ENTER.
При
вводе формулы массива Microsoft Excel
автоматически заключает ее в фигурные
скобки ({ }).
Для рассматриваемой задачи вычисления
обратной матрицы в каждой ячейке
выделенного диапазона будет одна и та
же формула {=МОБР(B44:D46)}.
В этом случае для ссылки на ячейки,
содержащие исходную матрицу, нельзя
использовать ни имя этой группы, ни
абсолютную адресацию.
Использование
формулы массива позволяет быстрее
ввести необходимые формулы, однако
запись становится менее наглядной,
поэтому ниже используется функция
ИНДЕКС.
Задание №12 решу ОГЭ 2022 математика 9 класс расчёты по формулам 50 тренировочных заданий с ответами и решением, сборник заданий составлен из всех возможных заданий ОГЭ 2022 по математике.
скачать задание №12 с ответами
Решу задание №12 ОГЭ математика 9 класс задания с ответами:

Некоторые задания (ответы выше)
1)Чтобы перевести значение температуры по шкале Цельсия (t, °C) в шкалу Фаренгейта (t, °F), пользуются формулой 1,8 32 F c t t, где C – градусы Цельсия, F – градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует 23º по шкале Цельсия?
2)Чтобы перевести значение температуры по шкале Цельсия (t, °C) в шкалу Фаренгейта (t, °F), пользуются формулой 1,8 32 F c t t, где C – градусы Цельсия, F – градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует 35º по шкале Цельсия?
3)Чтобы перевести значение температуры по шкале Цельсия (t, °C) в шкалу Фаренгейта (t, °F), пользуются формулой 5 32 9 с F t t, где C – градусы Цельсия, F – градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 149º по шкале Фаренгейта?
4)Чтобы перевести значение температуры по шкале Цельсия (t, °C) в шкалу Фаренгейта (t, °F), пользуются формулой 5 32 9 с F t t, где C – градусы Цельсия, F – градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 68º по шкале Фаренгейта?
5)Центростремительное ускорение при движении по окружности (в 2 м с/ ) можно вычислить по формуле 2 a R, где ω – угловая скорость (в с -1), а R – радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 8,5 с -1, а центростремительное ускорение равно 650,25 2 м с/ . Ответ дайте в метрах.
6)Центростремительное ускорение при движении по окружности (в 2 м с/ ) можно вычислить по формуле 2 a R , где ω – угловая скорость (в с -1), а R – радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 0,5 с -1, а центростремительное ускорение равно 1,75 2 м с/ . Ответ дайте в метрах.
7)Мощность постоянного тока (в ваттах) вычисляется по формуле 2 P I R , где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R, если мощность составляет 15,75 Вт, а сила тока равна 1,5 А. Ответ дайте в омах.
8)Мощность постоянного тока (в ваттах) вычисляется по формуле 2 P I R , где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R, если мощность составляет 541,5 Вт, а сила тока равна 9,5 А. Ответ дайте в омах.
9)В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С n 6500 4100 , где n – число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец.
10)В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С n 6500 4100 , где n – число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 10 колец.
11)В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С n 6500 4000 , где n – число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец.
12)В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С n 6500 4000 , где n – число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец
13)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле, где t – длительность поездки, выраженная в минутах (t > 5). Пользуясь этой формулой, рассчитайте стоимость 16-минутной поездки.
14)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле, где t – длительность поездки, выраженная в минутах (t > 5). Пользуясь этой формулой, рассчитайте стоимость 9-минутной поездки.
15)Площадь четырёхугольника можно вычислить по формуле, где d1 и d2 – длины диагоналей четырёхугольника,ь– угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1 = 14, sin 1 12, a S = 8,75.
16)Площадь четырёхугольника можно вычислить по формуле, где d1 и d2 – длины диагоналей четырёхугольника, – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 7, sin 2 7, a S = 4.
17)Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние S по формуле S n l , где n – число шагов, l – длина шага. Какое расстояние прошёл человек, если l = 70 см, n = 1400? Ответ выразите в километрах.
18)Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние S по формуле S n l , где n – число шагов, l – длина шага. Какое расстояние прошёл человек, если l = 50 см, n = 1200? Ответ выразите в километрах.
19)Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T l 2 , где l – длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунд.
20)Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T l2 , где l – длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 6 секунд.
Задание №9 ОГЭ 2022 по математике 9 класс с ответами
Задание 8 решу ОГЭ 2022 математика 9 класс 130 задач ответы с решением
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
В 12-ом задании мы сталкиваемся с прогрессиями — общими понятиями. Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые. Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.
Ответом в задании 12 является целое число или конечная десятичная дробь.
Теория к заданию №12
Начнем теоретическую справку об определениях прогрессий.
Арифметическая прогрессия:
Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.
an+1 = an + d
где d – разность прогрессии
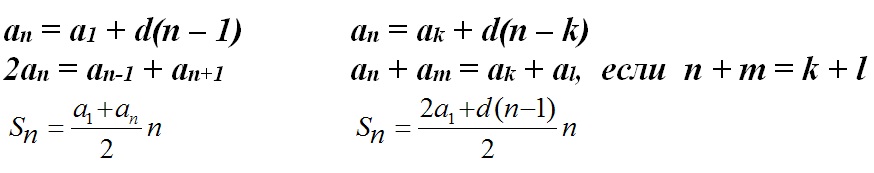
Геометрическая прогрессия:
Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.
bn+1 = bn q
где q – знаменатель прогрессии
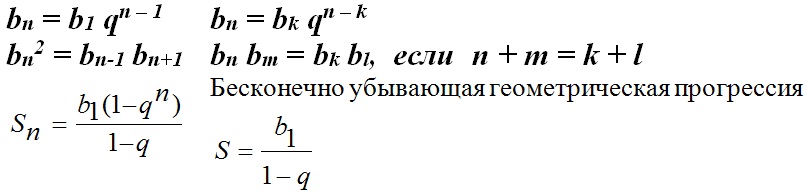
В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.
Разбор типовых вариантов задания №12 ОГЭ по математике.
Первый вариант задания (нахождение разности прогрессии)
Дана арифметическая прогрессия a(n) в которой
a (3) = 6,9
a (16) = 26,4
Найдите разность прогрессии.
Решение:
Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).
Находим разницу между значениями a (3) и a (16):
a (3) — a (16) = 26,4 — 6,9 = 19,5
Находим количество членов:
16 — 3 = 13
Находим разность прогрессии:
19,5 / 13 = 1,5
Ответ: 1,5
Второй вариант задания (нахождение неизвестного члена)
Выписано несколько последовательных членов геометрической прогрессии:
-1, x, -49, -343, ….
Найдите x.
Решение:
Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:
-343 / -49 = 7
Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.
x = -49 / 7 = -7
Ответ: -7
Третий вариант задания (нахождение n-ого члена)
Выписаны первые несколько членов арифметической прогрессии: 10, 6, 2, …
Найдите 101 член.
Решение:
Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:
an = a1 + (n-1) • d
В нашем случае:
a1 = 10
d = 6 — 10 = -4
Подставляем значения в формулу:
a101 = 10 + (101-1) • (-4) = -390
Ответ: -390
Демонстрационный вариант ОГЭ 2019
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение:
В данном задании нас проверяют на знание формулы арифметической прогрессии:
![]()
где n — номер члена прогрессии, d — разность, а а1 — первый член.
Решение:
Подставим в общую формулу известные из условия значения:
d = 4,
а1 = 6,
n = 15,
получим:
a15 = 6 + (15 — 1) • 4
вычислив, получаем значение 15 члена:
a15 = 62
Ответ: 62
Четвертый вариант задания (нахождение произвольного члена геометрической прогрессии)
Геометрическая прогрессия (bn) задана условиями:
b1=–2, bn+1=2bn.
Найдите b7.
Решение:
Искомый 7-й член прогрессии b7 будем искать по формуле:
b7=b1·q6. (1)
Здесь b1 по условию дано, а знаменатель q нет. Но его можно определить, исходя из определения этой величины. Согласно определению, q=bn+1/bn. Используя второе условие задачи, получим, что q=2.
Теперь используем 1-е условие задачи (b1=–2) и найдем искомую величину по формуле (1):
b7=–2·26=–2·64=–128.
Ответ: –128
Пятый вариант задания (нахождение суммы n членов геометрической прогрессии)
Выписаны первые три члена геометрической прогрессии: 1512; –252; 42; … Найдите сумму первых четырёх ее членов.
Решение:
Сумму произвольного кол-ва членов геометрич.прогрессии будем искать по формуле:
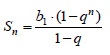
1-й член прогрессии известен из условия и равен b1=1512. Требуемое число членов n=4.
Знаменатель прогрессии найдем как частное двух соседних членов прогрессии (2-го и 1-го или 3-го и 2-го и т.д.). Найдем его так:
![]()
По условию b2=–252, b3=42, поэтому
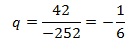
Отсюда получаем:
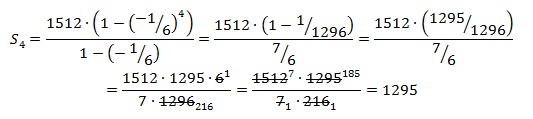
Ответ: 1295