Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 11
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
В задаче идет речь об арифметической прогрессии с первым членом a1 = 6 и разностью d = 4. Формула общего члена
an = a1 + d · (n – 1) = 6 + 4 · 14 = 62.
Ответ: 62.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Слайд 1
« Теория и практика по заданию 11 м атериалов ОГЭ » ГБОУ Школа №543 Московского района Санкт-Петербурга 2020 Учитель математики высшей категории Чагина Юлия Анатольевна Подготовка к ОГЭ по математике
Слайд 2
Теория В задачах 11 материалов ОГЭ проверяются навыки работы с тремя видами функций: Линейная у= кх + b График — прямая Квадратичная у=а + b х+с График — парабола Обратная пропорциональная зависимость у= График — гипербола
Слайд 3
Линейная функция Задается уравнением вида у= кх + b . Графиком функции является прямая. Коэффициенты к и b определяют расположение прямой на координатной плоскости.
Слайд 4
Коээфициент к: Определяет в какой координатной плоскости располагается прямая: к>0 Прямая находится в первой и третьей координатной четверти I Ш к
Слайд 5
Коэффициент B : Определяет смещение прямой вверх или вниз вдоль оси ординат ( Оу ) b >0 Прямая смещается вверх вдоль оси Оу на b единиц b { b
Слайд 6
Определите знак коэффициентов b и к у данной прямой Прямая проходит через I и III координатные четверти, значит коэффициент к>0 I III Прямая смещена вниз на четыре единицы вдоль оси ординат, значит b
Слайд 7
Определите знак коэффициентов b и к у данной прямой Прямая проходит через II и IV координатные четверти, значит коэффициент к 0 b {
Слайд 8
кВАДРАТИЧНАЯ функция Задается уравнением вида у=а + b х+с Графиком функции является парабола. Коэффициенты а , b и с определяют расположение прямой на координатной плоскости.
Слайд 9
Коээфициент а : Определяет направление ветвей параболы: а >0 Ветви параболы направлены вверх а
Слайд 10
Коээфициент В: Определяет смещение параболы вправо или влево вдоль оси абсцисс (Ох) b >0 Парабола смещена влево вдоль оси абсцисс { b >0 b
Слайд 11
Определят положение точки пересечения параболы с осью ординат ( Оу ) Коээфициент с : с >0 Парабола пересекает ось Оу в положительном направлении с >0 с
Слайд 12
Определите знаки коэффициентов а, b и с данной параболы Ветви параболы направлены вверх, значит коэффициент а>0 Парабола смещена вправо вдоль оси абсцисс, значит коэффициент b
Слайд 13
На одном из рисунков изображен график функции у= . Укажите номер этого рисунка. 1 2 3 4 у= а>0 — ветви параболы направленны вверх b
Слайд 14
Функция ОбратноЙ пропорциональнОЙ ЗАВИСИМОСТИ Задается уравнением вида у= Графиком функции является гипербола. Коэффициент, к определяет расположение прямой на координатной плоскости.
Слайд 15
Коээфициент к: к >0 Определяет расположение ветвей гиперболы в координатных четвертях Ветви гиперболы находятся в первой и третьей координатной четверти I III к
Слайд 16
Установите соответствие между графиками функций и формулами, которые их задают. Ответ: 314
Теория
| 1. | Линейная функция | |
| 2. | Функция обратной пропорциональности и модуля | |
| 3. | Квадратичная функция | |
| 4. | Как решать задание ОГЭ |
Задания
| 1. | Промежутки возрастания и убывания Сложность: | 1 |
| 2. | Формула функции Сложность: | 1 |
| 3. | Координаты точки пересечения с осями координат Сложность: | 2 |
| 4. | Вычисление вершины параболы Сложность: | 2 |
| 5. | Точка пересечения графиков функций Сложность: | 4 |
| 6. | Область определения функции Сложность: | 4 |
Экзаменационные задания (Я+)
| 1. | Как на ОГЭ (1). Графики элементарных функций Сложность: | 1 |
| 2. | Как на ОГЭ (2). Графики элементарных функций Сложность: | 1 |
| 3. | Как на ОГЭ (3). Графики элементарных функций Сложность: | 1 |
| 4. | Как на ОГЭ (4). Графики элементарных функций Сложность: | 1 |
Тесты
| 1. | Тренировка по теме Графики элементарных функций Сложность: среднее | 13 |
Материалы для учителей
Номер варианта сайта alexlarin.net:
Условие:
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Решение:
Пусть первое число равно (x,) тогда из первого свойства имеем три числа, которые образуют арифметическую прогрессию: (x, x+d, x+2d.)
Согласно второму условию имеем три другие числа, образующие геометрическую прогрессию: (x, x+d, 3x+3d.) Из свойства прогрессии имеем ((x+d)q=3x+3d Rightarrow q=3.)
Ответ 3.
Сегодня 22.01.2022 04:07 свежие новости час назад
Прогноз на сегодня : Задание 11 339114 огэ . Развитие событий.
Актуально сегодня (22.01.2022 04:07): Задание 11 339114 огэ
РЕШУ ОГЭ math oge.sdamgia. Ключ math oge.sdamgia .Вячеслав страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата после этого выплат не было..
1. Задание 11 339114 огэ
2. Задание 11 339114 огэ математика
3. Задание 11 номер 339114 огэ по математике
4. Задание 11 339114 огэ по русскому
5. Задание 11 339114 огэ по математике
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
9041462618282665b80f0416d63c2cfc 82b5696afc26f1c6d71f5bb37055a944
Задание 11 339114 огэ
Задание 11 339114 огэ
Задание 11 339114 огэ
кино игра престолов 1 сезон 9 серия | weather forecast clock 30221 инструкция на русском | океанами стали минусовка | firmware mts phone | стиральная машина aquamatic 1000t инструкция по применению | Инструкция по охране труда при работе по уборке территории | скачать образец акт дератизации животноводческих помещений | firmware for se a1723 | test by test 5 класс чесова ответы | разборка зеркала приора старого образца |
Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
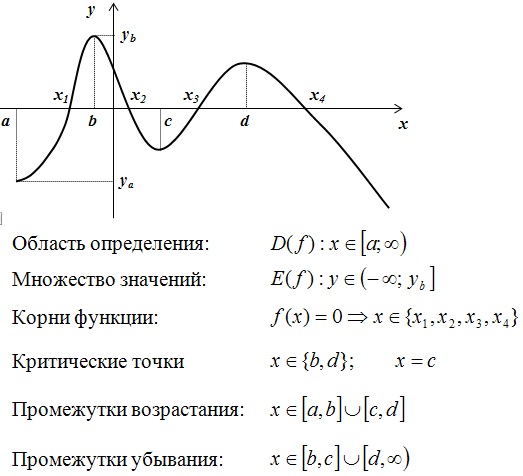
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
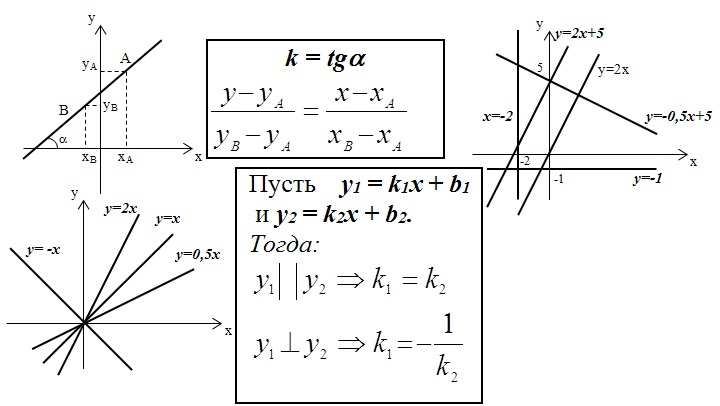
Рассмотрим случай квадратичной функции:
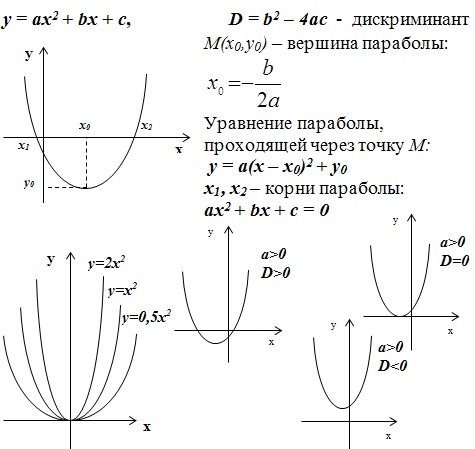
Также вспомним, что такое коренная функция и модуль:
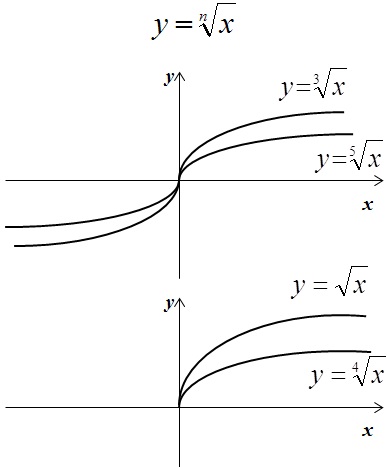

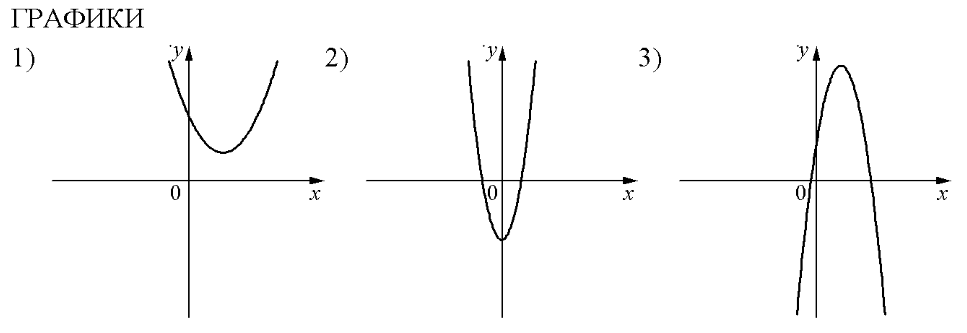
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
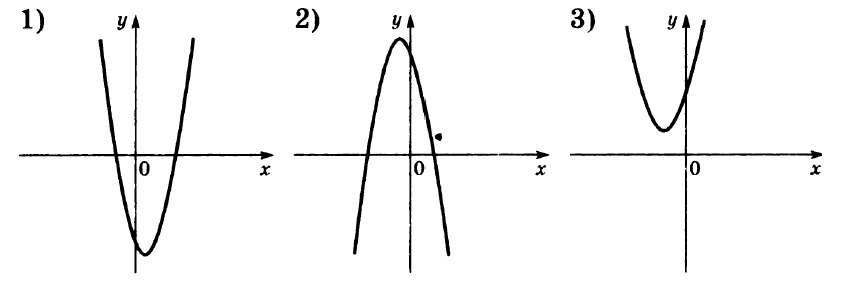
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
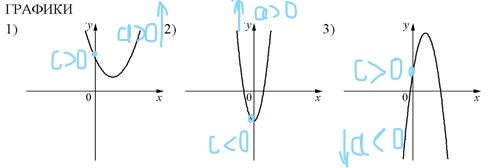
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №11 ОГЭ по математике.
Для выполнения задания 11 необходимо уметь строить и читать графики функций.
| Карточки для отработки задания 11 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 11 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 11 (презентация) Автор: Чагина Юлия Анатольевна → скачать |
Решение типовых задач № 11 на ОГЭ по математике
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе
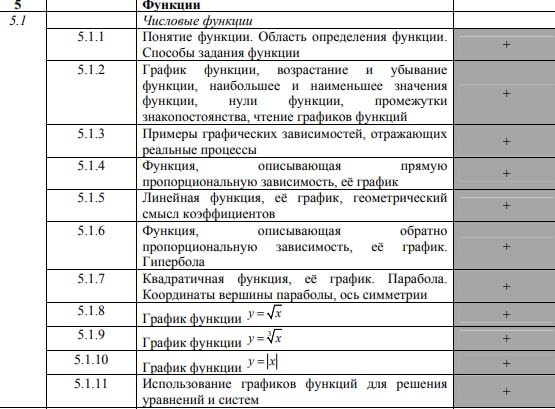
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Задание 9 ОГЭ по математике
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 10 ОГЭ по математике
1 слайд
Задание 11 Графики Заданиена установление соответствия между графиками функций и формулами, которые их задают.
3 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 231 А Б В А Б В 2 3 1
4 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 123 А Б В А Б В 1 2 3
7 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 321 2 3 1 А Б В
8 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
9 слайд
На рисунке изображены графики функций вида у= кх + b . Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
11 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
12 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
15 слайд
Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
16 слайд
Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
17 слайд
Установите соответствие между графиками функций и знаками с и D. В таблице под каждой буквой укажите соответствующий номер. А Б В
20 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 11
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
В задаче идет речь об арифметической прогрессии с первым членом a1 = 6 и разностью d = 4. Формула общего члена
an = a1 + d · (n – 1) = 6 + 4 · 14 = 62.
Ответ: 62.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Теория
| 1. | Линейная функция | |
| 2. | Функция обратной пропорциональности и модуля | |
| 3. | Квадратичная функция | |
| 4. | Как решать задание ОГЭ |
Задания
| 1. | Промежутки возрастания и убывания Сложность: | 1 |
| 2. | Формула функции Сложность: | 1 |
| 3. | Координаты точки пересечения с осями координат Сложность: | 2 |
| 4. | Вычисление вершины параболы Сложность: | 2 |
| 5. | Точка пересечения графиков функций Сложность: | 4 |
| 6. | Область определения функции Сложность: | 4 |
Экзаменационные задания (Я+)
| 1. | Как на ОГЭ (1). Графики элементарных функций Сложность: | 1 |
| 2. | Как на ОГЭ (2). Графики элементарных функций Сложность: | 1 |
| 3. | Как на ОГЭ (3). Графики элементарных функций Сложность: | 1 |
| 4. | Как на ОГЭ (4). Графики элементарных функций Сложность: | 1 |
Тесты
| 1. | Тренировка по теме Графики элементарных функций Сложность: среднее | 13 |
Материалы для учителей
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.
Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Задание 11 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.
Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член

Рассмотрим случай квадратичной функции:

Также вспомним, что такое коренная функция и модуль:


Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.
Разбор типовых вариантов задания №11 ОГЭ по математике
Первый вариант задания (параболы)
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:

Решение:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Второй вариант задания (гиперболы)
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

Решение:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Третий вариант задания (линейный график)
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Решение:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Демонстрационный вариант ОГЭ 2019
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Решение:
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
Ответ:
А 1
Б 3
В 2
Четвертый вариант задания (параболы)
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Решение:
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэф-т с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: A-1, Б-2, В-3
Пятый вариант задания (линейная функция)
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
Решение:
Рассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положит.направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: