Grand Hotel Paradox
Лучший тренинг в твоей жизни по развитию концептуального сознания в стиле Плохого Коуча. Поржать и задуматься. 30 дней веселья, осознания и перемен.
Не тормози
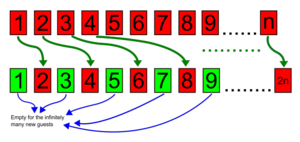
В 1920-е годы немецкий математик Дэвид Гильберт придумал известный мысленный эксперимент, чтобы показать, как сложно осознать концепцию бесконечности. Представьте отель с бесконечным количеством комнат и очень трудолюбивым ночным менеджером. Как-то ночью Бесконечный отель оказался полностью заполнен — всё было занято бесконечным количеством гостей. В отель входит мужчина и просит комнату. Вместо отказа ночной менеджер решает освободить для него комнату. Как? Просто. Он просит гостя из комнаты No1 переместиться в комнату No2, гостя из комнаты No2 — в комнату No3 и так далее. Каждый гость переезжает из комнаты n в комнату n+1. Поскольку количество комнат бесконечно, для каждого постояльца найдётся новая комната. А первая комната освободится для нового клиента.
Действия могут повторяться для любого конечного числа новых гостей. Если, скажем, туристический автобус привезёт 40 человек для размещения, тогда каждый постоялец просто переедет из комнаты n в комнату n+40, таким образом освобождая первые 40 комнат.
Теперь приезжает бесконечно большой автобус со счётным бесконечным количеством пассажиров, желающих снять комнаты. «Счётное бесконечное» — ключевое понятие. Автобус с бесконечным количеством пассажиров сначала сбивает с толку менеджера, но он находит способ разместить новых гостей. Он просит гостя из комнаты No 1 перейти во комнату No 2. Потом он просит гостя из комнаты No 2 переместиться в комнату No 4, гостя из комнаты No 3 — в комнату No 6 и так далее. Каждый постоялец переезжает из комнаты n в комнату 2n, заполняя только бесконечное количество чётных комнат. Таким образом, он освободил бесконечное количество нечётных номеров, которые потом занимают пассажиры бесконечного автобуса.
Все счастливы и гостиничный бизнес процветает лучше, чем когда-либо. Вообще, он процветает так же, как и всегда, принося бесконечное количество долларов за ночь. О потрясающем отеле разносятся слухи. Люди съезжаются отовсюду. Как-то ночью происходит невообразимое. Ночной менеджер смотрит на улицу и видит нескончаемую череду бесконечно больших автобусов со счётным бесконечным количеством пассажиров. Что же ему делать? Если он не найдёт для них комнат, отель понесёт бесконечные убытки, и он точно лишится работы. К счастью, он вспоминает, что примерно в 300 году до нашей эры Евклид доказал существование бесконечного количества простых чисел.
Чтобы выполнить, казалось бы, невозможное — найти бесконечные кровати для бесконечных автобусов с бесконечно усталыми путешественниками — ночной менеджер определяет каждого постояльца в комнату с номером первого простого числа — 2, возведённым в степень, равную номеру их настоящей комнаты. Так, постоялец из седьмой комнаты переходит в комнату 27 (два в седьмой степени), то есть в комнату No 128.
Ночной менеджер определяет пассажиров первого бесконечного автобуса в комнату с номером следующего простого числа — 3, возведённым в степень, равную номеру их автобусного места. Так, человек на месте с номером 7 в первом автобусе перейдёт в комнату с номером 37, то есть в комнату No 187. Так происходит со всеми в первом автобусе.
Пассажиры второго автобуса определяются в комнаты со степенями следующего простого числа — 5. Следующий автобус — со степенями 7. Каждый следующий автобус — со степенями 11, степенями 13, степенями 17 и так далее.
Так как в каждом таком числе только единица и степень с натуральным показателем простого числа могут быть множителями, то номерá комнат не совпадают. Все пассажиры автобусов распределяются по комнатам с помощью уникальной схемы определения комнат, основанной на уникальных простых числах. Так ночной менеджер может расселить каждого пассажира из каждого автобуса. Хотя останется множество незанятых комнат, таких как шестой номер, поскольку 6 не является степенью простого числа. К счастью, начальники не так хороши в математике, поэтому его должность в безопасности.
Схемы ночного менеджера возможны только потому, что хотя Бесконечный отель похож на логистический кошмар, он сталкивается с наименьшим уровнем бесконечности, главным образом со счётным бесконечным множеством натуральных чисел — 1, 2, 3, 4 и так далее. Георг Кантор назвал этот уровень бесконечности алеф-нуль. Мы используем натуральные числа для комнат и для номеров мест в автобусах. Используя высшие порядки бесконечности, такие как действительные числа, эти упорядоченные схемы были бы невозможны, потому что нельзя было бы всегда включать каждое число.
Бесконечный отель действительных чисел имеет «отрицательные» комнаты в подвале, дробные комнаты, поэтому мужчина в комнате No 1/2 подозревает, что него комната меньше, чем у гостя в комнате No 1. Комнаты квадратного корня, например, комната корня из двух, и комната Пи, где гости ожидают бесплатный пирог. Какой уважающий себя ночной менеджер вообще захочет там работать, даже за бесконечную зарплату? Но в Бесконечном отеле Гильберта, где никогда нет свободных мест, но всегда есть ещё одно — ситуации, с которыми сталкивается добросовестный и, возможно, слишком радушный менеджер, напоминают нам, как сложно нашим относительно ограниченным умам осознать такое огромное понятие, как бесконечность. Может, вы поможете решить эти проблемы после хорошего ночного сна. Но, если честно, нам может понадобиться поменять комнаты в 2 часа ночи.
Еще по теме:
- Вопросы, на которые пока нет ответов
- Еще 2 вопроса, на которые нет ответов
- Кот Шредингера
- Существует ли телекинез
- Эликсир молодости
- Парадокс Алле – теория рисков и принятия решений
- Эффект Даннинга – Крюгера
- Принцип Питера
Hilbert’s paradox of the Grand Hotel (colloquial: Infinite Hotel Paradox or Hilbert’s Hotel) is a thought experiment which illustrates a counterintuitive property of infinite sets. It is demonstrated that a fully occupied hotel with infinitely many rooms may still accommodate additional guests, even infinitely many of them, and this process may be repeated infinitely often. The idea was introduced by David Hilbert in a 1924 lecture «Über das Unendliche», reprinted in (Hilbert 2013, p.730), and was popularized through George Gamow’s 1947 book One Two Three… Infinity.[1][2]
The paradox[edit]
Consider a hypothetical hotel with a countably infinite number of rooms, all of which are occupied. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms, where the pigeonhole principle would apply.
Finitely many new guests[edit]
Suppose a new guest arrives and wishes to be accommodated in the hotel. We can (simultaneously) move the guest currently in room 1 to room 2, the guest currently in room 2 to room 3, and so on, moving every guest from their current room n to room n+1. After this, room 1 is empty and the new guest can be moved into that room. By repeating this procedure, it is possible to make room for any finite number of new guests. In general, assume that k guests seek a room. We can apply the same procedure and move every guest from room n to room n + k. In a similar manner, if k guests wished to leave the hotel, every guest moves from room n to room n − k.
Infinitely many new guests[edit]
It is also possible to accommodate a countably infinite number of new guests: just move the person occupying room 1 to room 2, the guest occupying room 2 to room 4, and, in general, the guest occupying room n to room 2n (2 times n), and all the odd-numbered rooms (which are countably infinite) will be free for the new guests.
Infinitely many coaches with infinitely many guests each[edit]
It is possible to accommodate countably infinitely many coachloads of countably infinite passengers each, by several different methods. Most methods depend on the seats in the coaches being already numbered (or use the axiom of countable choice). In general any pairing function can be used to solve this problem. For each of these methods, consider a passenger’s seat number on a coach to be , and their coach number to be , and the numbers and are then fed into the two arguments of the pairing function.
Prime powers method[edit]
Send the guest in room to room , then put the first coach’s load in rooms , the second coach’s load in rooms ; for coach number we use the rooms where is the th odd prime number. This solution leaves certain rooms empty (which may or may not be useful to the hotel); specifically, all numbers that are not prime powers, such as 15 or 847, will no longer be occupied. (So, strictly speaking, this shows that the number of arrivals is less than or equal to the number of vacancies created. It is easier to show, by an independent means, that the number of arrivals is also greater than or equal to the number of vacancies, and thus that they are equal, than to modify the algorithm to an exact fit.) (The algorithm works equally well if one interchanges and , but whichever choice is made, it must be applied uniformly throughout.)
Prime factorization method[edit]
Each person of a certain seat and coach can be put into room (presuming c=0 for the people already in the hotel, 1 for the first coach, etc.). Because every number has a unique prime factorization, it is easy to see all people will have a room, while no two people will end up in the same room. For example, the person in room 2592 () was sitting in on the 4th coach, on the 5th seat. Like the prime powers method, this solution leaves certain rooms empty.
This method can also easily be expanded for infinite nights, infinite entrances, etc. ( )
Interleaving method[edit]
For each passenger, compare the lengths of and as written in any positional numeral system, such as decimal. (Treat each hotel resident as being in coach #0.) If either number is shorter, add leading zeroes to it until both values have the same number of digits. Interleave the digits to produce a room number: its digits will be [first digit of coach number]-[first digit of seat number]-[second digit of coach number]-[second digit of seat number]-etc. The hotel (coach #0) guest in room number 1729 moves to room 01070209 (i.e., room 1,070,209). The passenger on seat 1234 of coach 789 goes to room 01728394 (i.e., room 1,728,394).
Unlike the prime powers solution, this one fills the hotel completely, and we can reconstruct a guest’s original coach and seat by reversing the interleaving process. First add a leading zero if the room has an odd number of digits. Then de-interleave the number into two numbers: the coach number consists of the odd-numbered digits and the seat number is the even-numbered ones. Of course, the original encoding is arbitrary, and the roles of the two numbers can be reversed (seat-odd and coach-even), so long as it is applied consistently.
Triangular number method[edit]
Those already in the hotel will be moved to room , or the th triangular number. Those in a coach will be in room , or the triangular number plus . In this way all the rooms will be filled by one, and only one, guest.
This pairing function can be demonstrated visually by structuring the hotel as a one-room-deep, infinitely tall pyramid. The pyramid’s topmost row is a single room: room 1; its second row is rooms 2 and 3; and so on. The column formed by the set of rightmost rooms will correspond to the triangular numbers. Once they are filled (by the hotel’s redistributed occupants), the remaining empty rooms form the shape of a pyramid exactly identical to the original shape. Thus, the process can be repeated for each infinite set. Doing this one at a time for each coach would require an infinite number of steps, but by using the prior formulas, a guest can determine what their room «will be» once their coach has been reached in the process, and can simply go there immediately.
Arbitrary enumeration method[edit]
Let . is countable since is countable, hence we may enumerate its elements . Now if , assign the th guest of the th coach to the th room (consider the guests already in the hotel as guests of the th coach). Thus we have a function assigning each person to a room; furthermore, this assignment does not skip over any rooms.
Further layers of infinity[edit]
Suppose the hotel is next to an ocean, and an infinite number of car ferries arrive, each bearing an infinite number of coaches, each with an infinite number of passengers. This is a situation involving three «levels» of infinity, and it can be solved by extensions of any of the previous solutions.
The prime factorization method can be applied by adding a new prime number for every additional layer of infinity ( , with the ferry).
The prime power solution can be applied with further exponentiation of prime numbers, resulting in very large room numbers even given small inputs. For example, the passenger in the second seat of the third bus on the second ferry (address 2-3-2) would raise the 2nd odd prime (5) to 49, which is the result of the 3rd odd prime (7) being raised to the power of his seat number (2). This room number would have over thirty decimal digits.
The interleaving method can be used with three interleaved «strands» instead of two. The passenger with the address 2-3-2 would go to room 232, while the one with the address 4935-198-82217 would go to room #008,402,912,391,587 (the leading zeroes can be removed).
Anticipating the possibility of any number of layers of infinite guests, the hotel may wish to assign rooms such that no guest will need to move, no matter how many guests arrive afterward. One solution is to convert each arrival’s address into a binary number in which ones are used as separators at the start of each layer, while a number within a given layer (such as a guest’s coach number) is represented with that many zeroes. Thus, a guest with the prior address 2-5-1-3-1 (five infinite layers) would go to room 10010000010100010 (decimal 295458).
As an added step in this process, one zero can be removed from each section of the number; in this example, the guest’s new room is 101000011001 (decimal 2585). This ensures that every room could be filled by a hypothetical guest. If no infinite sets of guests arrive, then only rooms that are a power of two will be occupied.
Infinite layers of nesting[edit]
Although a room can be found for any finite number of nested infinities of people, the same is not always true for an infinite number of layers, even if a finite number of elements exists at each layer.
Analysis[edit]
Hilbert’s paradox is a veridical paradox: it leads to a counter-intuitive result that is provably true. The statements «there is a guest to every room» and «no more guests can be accommodated» are not equivalent when there are infinitely many rooms.
Initially, this state of affairs might seem to be counter-intuitive. The properties of infinite collections of things are quite different from those of finite collections of things. The paradox of Hilbert’s Grand Hotel can be understood by using Cantor’s theory of transfinite numbers. Thus, in an ordinary (finite) hotel with more than one room, the number of odd-numbered rooms is obviously smaller than the total number of rooms. However, in Hilbert’s aptly named Grand Hotel, the quantity of odd-numbered rooms is not smaller than the total «number» of rooms. In mathematical terms, the cardinality of the subset containing the odd-numbered rooms is the same as the cardinality of the set of all rooms. Indeed, infinite sets are characterized as sets that have proper subsets of the same cardinality. For countable sets (sets with the same cardinality as the natural numbers) this cardinality is .[3]
Rephrased, for any countably infinite set, there exists a bijective function which maps the countably infinite set to the set of natural numbers, even if the countably infinite set contains the natural numbers. For example, the set of rational numbers—those numbers which can be written as a quotient of integers—contains the natural numbers as a subset, but is no bigger than the set of natural numbers since the rationals are countable: there is a bijection from the naturals to the rationals.
References in fiction[edit]
- BBC Learning Zone repeatedly screened a 1996 one-off educational docudrama Hotel Hilbert set in the hotel as seen through the eyes of a young female guest Fiona Knight, her name a pun on «finite». The programme was designed to educate viewers about the concept of infinity.[4]
- The novel White Light by mathematician/science fiction writer Rudy Rucker includes a hotel based on Hilbert’s paradox, and where the protagonist of the story meets Georg Cantor.
- Stephen Baxter’s science fiction novel Transcendent has a brief discussion on the nature of infinity, with an explanation based on the paradox, modified to use soldiers rather than hotels.
- Geoffrey A. Landis’ Nebula Award-winning short story «Ripples in the Dirac Sea» uses the Hilbert hotel as an explanation of why an infinitely-full Dirac sea can nevertheless still accept particles.
- In Peter Høeg’s novel Miss Smilla’s Feeling for Snow, the titular heroine reflects that it is admirable for the hotel’s manager and guests to go to all that trouble so that the latecomer can have his own room and some privacy.
- In Ivar Ekeland’s novel for children, The Cat in Numberland, a «Mr. Hilbert» and his wife run an infinite hotel for all the integers. The story progresses through the triangular method for the rationals.
- In Will Wiles’s novel The Way Inn, about an infinitely large motel, the villain’s name is Hilbert.
- In Reginald Hill’s novel «The Stranger House» the character Sam refers to the Hilbert Hotel paradox.
- The short story by Naum Ya. Vilenkin The Extraordinary Hotel (often erroneously attributed to Stanislaw Lem) shows the way in which Hilbert’s Grand Hotel may be reshuffled when infinite new hosts arrive.
- The comic book saga The Tempest from the League of Extraordinary Gentlemen series by Alan Moore and Kevin O’Neill shows a villain called Infinity. In the story it is suggested that the villain goes to the hotel based on Hilbert’s paradox. Georg Cantor is mentioned as well.
See also[edit]
- List of paradoxes – List of statements that appear to contradict themselves
- Banach–Tarski paradox – Taking apart an object and constructing two identical copies of it from the pieces
- Galileo’s paradox
- Paradoxes of set theory
- Pigeonhole principle – If there are more items than boxes holding them, one box must contain at least two items
References[edit]
- ^ Kragh, Helge (2014). «The True (?) Story of Hilbert’s Infinite Hotel». arXiv:1403.0059 [physics.hist-ph].
- ^ Gamow, George (1947). One Two Three… Infinity: Facts and Speculations of Science. New York: Viking Press. p. 17.
- ^ Rucker, Rudy (1984) [1982]. Infinity and the Mind. The Science and Philosophy of the Infinite. Paladin. pp. 73–78. ISBN 0-586-08465-7.
- ^ «Hotel Hilbert». IMDb.
- Hilbert, David (2013), Ewald, William; Sieg, Wilfried (eds.), David Hilbert’s Lectures on the Foundations of Arithmetics and Logic 1917-1933, Heidelberg: Springer-Verlag, doi:10.1007/978-3-540-69444-1, ISBN 978-3-540-20578-4
External links[edit]
- Hilbert infinite hotel. M. Hazewinkel. Encyclopedia of Mathematics, Springer. Accessed May 25, 2007.
- Nancy Casey, Welcome to the Hotel Infinity! — The paradox told as a humorous narrative, featuring a hotel owner and a building contractor based on the feuding 19th-century mathematicians Georg Cantor and Leopold Kronecker
- Steven Strogatz, The Hilbert Hotel, NY Times, May 9, 2010
- Hilbert’s Infinite Hotel, h2g2
- The Hilbert Hotel — YouTube presentation
- «Beyond the Finite»
- The Infinite Hotel Paradox — Jeff Dekofsky — TED-Ed Lessons
Hilbert’s paradox of the Grand Hotel (colloquial: Infinite Hotel Paradox or Hilbert’s Hotel) is a thought experiment which illustrates a counterintuitive property of infinite sets. It is demonstrated that a fully occupied hotel with infinitely many rooms may still accommodate additional guests, even infinitely many of them, and this process may be repeated infinitely often. The idea was introduced by David Hilbert in a 1924 lecture «Über das Unendliche», reprinted in (Hilbert 2013, p.730), and was popularized through George Gamow’s 1947 book One Two Three… Infinity.[1][2]
The paradox[edit]
Consider a hypothetical hotel with a countably infinite number of rooms, all of which are occupied. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms, where the pigeonhole principle would apply.
Finitely many new guests[edit]
Suppose a new guest arrives and wishes to be accommodated in the hotel. We can (simultaneously) move the guest currently in room 1 to room 2, the guest currently in room 2 to room 3, and so on, moving every guest from their current room n to room n+1. After this, room 1 is empty and the new guest can be moved into that room. By repeating this procedure, it is possible to make room for any finite number of new guests. In general, assume that k guests seek a room. We can apply the same procedure and move every guest from room n to room n + k. In a similar manner, if k guests wished to leave the hotel, every guest moves from room n to room n − k.
Infinitely many new guests[edit]
It is also possible to accommodate a countably infinite number of new guests: just move the person occupying room 1 to room 2, the guest occupying room 2 to room 4, and, in general, the guest occupying room n to room 2n (2 times n), and all the odd-numbered rooms (which are countably infinite) will be free for the new guests.
Infinitely many coaches with infinitely many guests each[edit]
It is possible to accommodate countably infinitely many coachloads of countably infinite passengers each, by several different methods. Most methods depend on the seats in the coaches being already numbered (or use the axiom of countable choice). In general any pairing function can be used to solve this problem. For each of these methods, consider a passenger’s seat number on a coach to be , and their coach number to be , and the numbers and are then fed into the two arguments of the pairing function.
Prime powers method[edit]
Send the guest in room to room , then put the first coach’s load in rooms , the second coach’s load in rooms ; for coach number we use the rooms where is the th odd prime number. This solution leaves certain rooms empty (which may or may not be useful to the hotel); specifically, all numbers that are not prime powers, such as 15 or 847, will no longer be occupied. (So, strictly speaking, this shows that the number of arrivals is less than or equal to the number of vacancies created. It is easier to show, by an independent means, that the number of arrivals is also greater than or equal to the number of vacancies, and thus that they are equal, than to modify the algorithm to an exact fit.) (The algorithm works equally well if one interchanges and , but whichever choice is made, it must be applied uniformly throughout.)
Prime factorization method[edit]
Each person of a certain seat and coach can be put into room (presuming c=0 for the people already in the hotel, 1 for the first coach, etc.). Because every number has a unique prime factorization, it is easy to see all people will have a room, while no two people will end up in the same room. For example, the person in room 2592 () was sitting in on the 4th coach, on the 5th seat. Like the prime powers method, this solution leaves certain rooms empty.
This method can also easily be expanded for infinite nights, infinite entrances, etc. ( )
Interleaving method[edit]
For each passenger, compare the lengths of and as written in any positional numeral system, such as decimal. (Treat each hotel resident as being in coach #0.) If either number is shorter, add leading zeroes to it until both values have the same number of digits. Interleave the digits to produce a room number: its digits will be [first digit of coach number]-[first digit of seat number]-[second digit of coach number]-[second digit of seat number]-etc. The hotel (coach #0) guest in room number 1729 moves to room 01070209 (i.e., room 1,070,209). The passenger on seat 1234 of coach 789 goes to room 01728394 (i.e., room 1,728,394).
Unlike the prime powers solution, this one fills the hotel completely, and we can reconstruct a guest’s original coach and seat by reversing the interleaving process. First add a leading zero if the room has an odd number of digits. Then de-interleave the number into two numbers: the coach number consists of the odd-numbered digits and the seat number is the even-numbered ones. Of course, the original encoding is arbitrary, and the roles of the two numbers can be reversed (seat-odd and coach-even), so long as it is applied consistently.
Triangular number method[edit]
Those already in the hotel will be moved to room , or the th triangular number. Those in a coach will be in room , or the triangular number plus . In this way all the rooms will be filled by one, and only one, guest.
This pairing function can be demonstrated visually by structuring the hotel as a one-room-deep, infinitely tall pyramid. The pyramid’s topmost row is a single room: room 1; its second row is rooms 2 and 3; and so on. The column formed by the set of rightmost rooms will correspond to the triangular numbers. Once they are filled (by the hotel’s redistributed occupants), the remaining empty rooms form the shape of a pyramid exactly identical to the original shape. Thus, the process can be repeated for each infinite set. Doing this one at a time for each coach would require an infinite number of steps, but by using the prior formulas, a guest can determine what their room «will be» once their coach has been reached in the process, and can simply go there immediately.
Arbitrary enumeration method[edit]
Let . is countable since is countable, hence we may enumerate its elements . Now if , assign the th guest of the th coach to the th room (consider the guests already in the hotel as guests of the th coach). Thus we have a function assigning each person to a room; furthermore, this assignment does not skip over any rooms.
Further layers of infinity[edit]
Suppose the hotel is next to an ocean, and an infinite number of car ferries arrive, each bearing an infinite number of coaches, each with an infinite number of passengers. This is a situation involving three «levels» of infinity, and it can be solved by extensions of any of the previous solutions.
The prime factorization method can be applied by adding a new prime number for every additional layer of infinity ( , with the ferry).
The prime power solution can be applied with further exponentiation of prime numbers, resulting in very large room numbers even given small inputs. For example, the passenger in the second seat of the third bus on the second ferry (address 2-3-2) would raise the 2nd odd prime (5) to 49, which is the result of the 3rd odd prime (7) being raised to the power of his seat number (2). This room number would have over thirty decimal digits.
The interleaving method can be used with three interleaved «strands» instead of two. The passenger with the address 2-3-2 would go to room 232, while the one with the address 4935-198-82217 would go to room #008,402,912,391,587 (the leading zeroes can be removed).
Anticipating the possibility of any number of layers of infinite guests, the hotel may wish to assign rooms such that no guest will need to move, no matter how many guests arrive afterward. One solution is to convert each arrival’s address into a binary number in which ones are used as separators at the start of each layer, while a number within a given layer (such as a guest’s coach number) is represented with that many zeroes. Thus, a guest with the prior address 2-5-1-3-1 (five infinite layers) would go to room 10010000010100010 (decimal 295458).
As an added step in this process, one zero can be removed from each section of the number; in this example, the guest’s new room is 101000011001 (decimal 2585). This ensures that every room could be filled by a hypothetical guest. If no infinite sets of guests arrive, then only rooms that are a power of two will be occupied.
Infinite layers of nesting[edit]
Although a room can be found for any finite number of nested infinities of people, the same is not always true for an infinite number of layers, even if a finite number of elements exists at each layer.
Analysis[edit]
Hilbert’s paradox is a veridical paradox: it leads to a counter-intuitive result that is provably true. The statements «there is a guest to every room» and «no more guests can be accommodated» are not equivalent when there are infinitely many rooms.
Initially, this state of affairs might seem to be counter-intuitive. The properties of infinite collections of things are quite different from those of finite collections of things. The paradox of Hilbert’s Grand Hotel can be understood by using Cantor’s theory of transfinite numbers. Thus, in an ordinary (finite) hotel with more than one room, the number of odd-numbered rooms is obviously smaller than the total number of rooms. However, in Hilbert’s aptly named Grand Hotel, the quantity of odd-numbered rooms is not smaller than the total «number» of rooms. In mathematical terms, the cardinality of the subset containing the odd-numbered rooms is the same as the cardinality of the set of all rooms. Indeed, infinite sets are characterized as sets that have proper subsets of the same cardinality. For countable sets (sets with the same cardinality as the natural numbers) this cardinality is .[3]
Rephrased, for any countably infinite set, there exists a bijective function which maps the countably infinite set to the set of natural numbers, even if the countably infinite set contains the natural numbers. For example, the set of rational numbers—those numbers which can be written as a quotient of integers—contains the natural numbers as a subset, but is no bigger than the set of natural numbers since the rationals are countable: there is a bijection from the naturals to the rationals.
References in fiction[edit]
- BBC Learning Zone repeatedly screened a 1996 one-off educational docudrama Hotel Hilbert set in the hotel as seen through the eyes of a young female guest Fiona Knight, her name a pun on «finite». The programme was designed to educate viewers about the concept of infinity.[4]
- The novel White Light by mathematician/science fiction writer Rudy Rucker includes a hotel based on Hilbert’s paradox, and where the protagonist of the story meets Georg Cantor.
- Stephen Baxter’s science fiction novel Transcendent has a brief discussion on the nature of infinity, with an explanation based on the paradox, modified to use soldiers rather than hotels.
- Geoffrey A. Landis’ Nebula Award-winning short story «Ripples in the Dirac Sea» uses the Hilbert hotel as an explanation of why an infinitely-full Dirac sea can nevertheless still accept particles.
- In Peter Høeg’s novel Miss Smilla’s Feeling for Snow, the titular heroine reflects that it is admirable for the hotel’s manager and guests to go to all that trouble so that the latecomer can have his own room and some privacy.
- In Ivar Ekeland’s novel for children, The Cat in Numberland, a «Mr. Hilbert» and his wife run an infinite hotel for all the integers. The story progresses through the triangular method for the rationals.
- In Will Wiles’s novel The Way Inn, about an infinitely large motel, the villain’s name is Hilbert.
- In Reginald Hill’s novel «The Stranger House» the character Sam refers to the Hilbert Hotel paradox.
- The short story by Naum Ya. Vilenkin The Extraordinary Hotel (often erroneously attributed to Stanislaw Lem) shows the way in which Hilbert’s Grand Hotel may be reshuffled when infinite new hosts arrive.
- The comic book saga The Tempest from the League of Extraordinary Gentlemen series by Alan Moore and Kevin O’Neill shows a villain called Infinity. In the story it is suggested that the villain goes to the hotel based on Hilbert’s paradox. Georg Cantor is mentioned as well.
See also[edit]
- List of paradoxes – List of statements that appear to contradict themselves
- Banach–Tarski paradox – Taking apart an object and constructing two identical copies of it from the pieces
- Galileo’s paradox
- Paradoxes of set theory
- Pigeonhole principle – If there are more items than boxes holding them, one box must contain at least two items
References[edit]
- ^ Kragh, Helge (2014). «The True (?) Story of Hilbert’s Infinite Hotel». arXiv:1403.0059 [physics.hist-ph].
- ^ Gamow, George (1947). One Two Three… Infinity: Facts and Speculations of Science. New York: Viking Press. p. 17.
- ^ Rucker, Rudy (1984) [1982]. Infinity and the Mind. The Science and Philosophy of the Infinite. Paladin. pp. 73–78. ISBN 0-586-08465-7.
- ^ «Hotel Hilbert». IMDb.
- Hilbert, David (2013), Ewald, William; Sieg, Wilfried (eds.), David Hilbert’s Lectures on the Foundations of Arithmetics and Logic 1917-1933, Heidelberg: Springer-Verlag, doi:10.1007/978-3-540-69444-1, ISBN 978-3-540-20578-4
External links[edit]
- Hilbert infinite hotel. M. Hazewinkel. Encyclopedia of Mathematics, Springer. Accessed May 25, 2007.
- Nancy Casey, Welcome to the Hotel Infinity! — The paradox told as a humorous narrative, featuring a hotel owner and a building contractor based on the feuding 19th-century mathematicians Georg Cantor and Leopold Kronecker
- Steven Strogatz, The Hilbert Hotel, NY Times, May 9, 2010
- Hilbert’s Infinite Hotel, h2g2
- The Hilbert Hotel — YouTube presentation
- «Beyond the Finite»
- The Infinite Hotel Paradox — Jeff Dekofsky — TED-Ed Lessons
В начале двадцатого века Гёттингенский университет в Герамании (University of Göttingen) был одним из лучших исследовательских центров по математике в мире. Математик Дэвид Гильберт был хорошо зарекомендовавшим себя профессором в этом университете. Зимой 1924-1925 годов он дал серию лекций о бесконечности в математике, физике и астрономии. В одной из этих лекций он использовал пример, чтобы объяснить решающее различие между конечными и бесконечными множествами. Пример этот, принято сейчас называть отель Гильберта.
Отель Гильберта
Отель Гильберта — воображаемое здание, в котором имеется бесконечное количество комнат. Управляющий отелем гордится тем, что никогда не отказал ни одному гостю. А теперь представьте себе: поздним вечером, когда все номера отеля заняты, внезапно появляется новый гость.
Портье идет к управляющему и сообщает ему, что гостя некуда поселить. Управляющий говорит, что надо попросить всех жильцов переселиться в номер по соседству, так что гость из первого номера переселяется во второй, гость из второго — в третий и так далее. После этого первая комната освободится, и туда можно будет поселить нового гостя.
Однако в полночь портье снова прибегает к управляющему. На этот раз он просто в отчаянии. Только что для участия в симпозиуме прибыло бесконечное количество математиков. «Мы же не сможем поселить их всех!» — восклицает портье. Подумав немного, управляющий предлагает следующее: «Нам придется попросить наших гостей о еще одном одолжении. Пусть каждый умножит номер своей комнаты на два и переселится в комнату с полученным номером». Таким образом, гость из четвертого номера переселяется в комнату 8, гость из комнаты 23 — в комнату 46, гость из комнаты 352 — в комнату 704 и так далее. После этого все комнаты с нечетными номерами освободятся. В них и поселятся участники симпозиума.
Этот прекрасный пример, показывающий красоту бесконечности популяризировал Джордж Гамов в своей научно-популярной книге 1947 года «Один два три … Бесконечность: Факты и Размышления о Науке» (George Gamow. One Two Three…Infinity: Facts and Speculations of Science).
Для тех кому интересно почитать о развитии идеи Отеля Гильберта я советую статью Аны Риты Пирес «Гостеприимство в отеле Гильберт. Насколько велика бесконечность?» (Ana Rita Pires «Hospitality at the Hilbert Hotel. How big is infinity?»). В этой статье Ана Пирес рассуждает о том, как разместятся гости, если они приехали на 99 автобусах с бесконечным числом мест, а также если приехало бесконечно число автобусов с бесконечным числом пассажиров. И даже еще сильнее развивает эту мысль, рассуждая о многомерном бесконечно пространстве.
Автор: Наталья Станиславовна
Частный преподаватель по математике.
Репетитор по математике в г. Екатеринбург.
Телефон: +7 900 200 34 43
Гостиница Гильберта. Ответ
Эту задачу предложил немецкий математик Давид Гильберт где то в третьем десятилетии 20 века. Давид был одним из величайших умов своего времени. Среди большого числа его учеников, которые в последствии стали видными учеными, был Джон Фон Нейман. Он так же консультировал Эйнштейна при разработке тензорного анализа — фундамента теории относительности.
Один гость
Напомню вам условие задачи для одного гостя из предыдущей статьи:
Представьте себе гостиницу с бесконечным числом комнат. Комнаты пронумерованы натуральными числами, от 1 до ∞. В один прекрасный день в нашу гостиницу вошел человек и попросил снять комнату. К сожалению, для нашего гостя не нашлось комнаты, так как именно в этот день отель был полностью заполнен бесконечным числом гостей. Выгнать гостя? Или все же есть возможность предоставить ему свободную комнату не выселяя никого из постояльцев?
Бесконечное число гостей
Если вы смогли найти комнату для одного гостя значит вы замечательный администратор. Но всегда есть простор для улучшения ваших навыков. Представьте что в полностью заполненный бесконечный отель приехало бесконечное число гостей. Как бы вы поселили бесконечное число гостей, при этом не выселяя никого из бесконечного числа постояльцев?
Четное число — целое число, которое делится без остатка на 2.
Этот парадокс хорош тем, что он отлично показывает странные, но вполне логичные свойства бесконечности в простых и понятных сущностях. Посмотрите так же этот интересный ролик:
Источник
Парадоксы бесконечности: Отель Гильберта
Отель Гильберта
Отель Гильберта – воображаемое здание, в котором имеется бесконечное количество комнат. Управляющий отелем гордится тем, что никогда не отказал ни одному гостю. А теперь представьте себе: поздним вечером, когда все номера отеля заняты, внезапно появляется новый гость.
Портье идет к управляющему и сообщает ему, что гостя некуда поселить. Управляющий говорит, что надо попросить всех жильцов переселиться в номер по соседству, так что гость из первого номера переселяется во второй, гость из второго – в третий и так далее. После этого первая комната освободится, и туда можно будет поселить нового гостя.
Однако в полночь портье снова прибегает к управляющему. На этот раз он просто в отчаянии. Только что для участия в симпозиуме прибыло бесконечное количество математиков. «Мы же не сможем поселить их всех!» – восклицает портье. Подумав немного, управляющий предлагает следующее: «Нам придется попросить наших гостей о еще одном одолжении. Пусть каждый умножит номер своей комнаты на два и переселится в комнату с полученным номером». Таким образом, гость из четвертого номера переселяется в комнату 8, гость из комнаты 23 – в комнату 46, гость из комнаты 352 – в комнату 704 и так далее. После этого все комнаты с нечетными номерами освободятся. В них и поселятся участники симпозиума.
Этот прекрасный пример, показывающий красоту бесконечности популяризировал Джордж Гамов в своей научно-популярной книге 1947 года “Один два три … Бесконечность: Факты и Размышления о Науке” (George Gamow. One Two Three…Infinity: Facts and Speculations of Science).
Для тех кому интересно почитать о развитии идеи Отеля Гильберта я советую статью Аны Риты Пирес “Гостеприимство в отеле Гильберт. Насколько велика бесконечность?” (Ana Rita Pires “Hospitality at the Hilbert Hotel. How big is infinity?”). В этой статье Ана Пирес рассуждает о том, как разместятся гости, если они приехали на 99 автобусах с бесконечным числом мест, а также если приехало бесконечно число автобусов с бесконечным числом пассажиров. И даже еще сильнее развивает эту мысль, рассуждая о многомерном бесконечно пространстве.
Источник
Petruchek.Info
Бесконечный отель
В отеле «Infinity» проходит межгалактический слёт гуманоидов и негуманоидов.
Все номера заняты (т.е. в каждом номере есть постоялец).
Нельзя селить в один номер нескольких постояльцев. Постояльцев можно переселять, сообщив переселяемому его новый номер.
Однако по сути расселение в бесконечное количество комнат ничем не отличается от этого круга.
Т.к. все комнаты заняты, а рассление дополнительных желающих заключается в переселении людей в другие комнаты, в которых уже кто-то живет и тоже вынужден переселяться.
Не надо выдумывать того, что не указано в условии задачи: прибавляются только гости, комнат сколько и было, столько и осталось.
Время здесь ни при чём.
Смысл задачи — в иллюстрации ответа на вопросы:
1) каких чисел больше: натуральных, больших двух (3,4,5. ) или всех натуральных (1,2,3. )?
2) каких чисел больше: натуральных (1,2,3. ) или чётных натуральных (2,4,6. )?
Отдельно можно подумать над тем, каких чисел больше: натуральных (1,2,3) или действительных на отрезке [0,1].
Ну, если интересно почитать, то ключевые слова — «счётность множеств», «континуум».
Вкратце: натуральных чисел столько же, сколько чётных, и столько же, сколько нечётных. «Является подмножеством» в данном случае не является критерием. Рациональных чисел (это те, которые представимы в виде дроби вида p/q) столько же, сколько и натуральных.
Если элементы какого-либо бесконечного множества можно «занумеровать», или «посчитать», то этих элементов столько же, сколько и натуральных чисел.
А вот действительных чисел на отрезке [0,1] больше, чем всех натуральных.
Эти вопросы изучаются в математическом анализе, там интересно.
Источник
Парадокс «Гранд-отель»
ПРОЛОГ
«Хочешь поиграть в пазлы?» — спросила мама своего 8-летнего ребёнка. «Конечно, мамочка!» — ответило дитя.
Все мы любим головоломки. И забавно, что эта любовь не имеет возрастных границ. С возрастом мы так же любим поломать голову над какой-нибудь сложной загадкой, а когда наконец приходим к её отгадке, хочется прыгать от радости и поделиться ею со всем миром. Эта статья посвящена головоломке, основанной на математическом парадоксе.
«И сказал Бог: да будет свет. И стал свет». (Третий стих книги Бытия)
ВОТ ТАКАЯ ГОЛОВОЛОМКА
В чём суть этого парадокса «Гранд-отель»?
Предположим, что на планете Титан есть отель со счётным бесконечным множеством номеров, начиная от первого и до бесконечности. Счётное множество является бесконечным, если оно имеет взаимно-однозначное соответствие с натуральными числами, такими как 1, 2, 3 и так далее до бесконечности.Этот отель известен на всю Вселенную. Каждый вечер в нём останавливается бесчисленное количество людей. И вот однажды отель оказался заполнен постояльцами. Теперь управляющий отеля ломает голову над тем, где разместить будущих посетителей.
Так сложно и в то же время так просто O(FINITE)
Тут открылись главные ворота.Управляющий поднял взгляд и застыл в изумлении.За всю свою жизнь он не видел такой очаровательной и ослепительной дамы.Она подошла к стойке администратора и сказала: «Монсеньор, меня зовут Мяяяу.Я — представитель планеты Р-616 из Шелковистой Галактики.Ваш отель знаменит на всю Вселенную, поэтому я решила остаться здесь на ночь.Не могли бы Вы выдать мне ключ-карту от моего номера?».
Так как это бесконечный отель, в нём всегда остаётся ещё один номер для заселения. Но управляющий не может предоставить ей любой номер, так как все гостиничные номера (не только 1-й, 2-й, 3-й, но и, скажем, 1284742018764398976755836-й) уже заняты. Так неужели заселить её в отель не получится? Было бы обидно отказать такой красотке 😉 Ну, конечно же, управляющий найдёт ей номер. А теперь оторвитесь от чтения, сделайте паузу и немного подумайте.
Предположим, мы попросим её занять первый номер. Но он ведь уже занят, верно? Куда девать его постояльца? Мы попросим его переселиться во второй номер, а постояльца второго номера — в третий и так далее. Таким образом, все постояльцы переселяются каждый в следующий, соседний номер. То есть в общем случае постоялец из номера N переселится в номер (N + 1). Но отель ведь бесконечный и всегда остаётся ещё один номер, поэтому ни у кого проблем с заселением не возникнет.
Следовательно, применяя такую логику перемещения постояльцев из одного номера в другой, можно для любого конечного числа прибывающих посетителей отеля найти номера для заселения. Если в отель прибыли M посетителей, то первые M номеров можно освободить, переселив каждого постояльца из номера N в номер (N + M). В таком случае эти М освободившихся номеров смогут занять M вновь прибывших посетителей.
На один уровень сложнее O(INFINITE)
Мяяяу очень понравилось её пребывание в бесконечном отеле.Два месяца спустя, в рождественский сочельник, она появилась снова, но уже не одна, а со всеми жителями своей планеты, прилетев на специальном звездолёте!И все они хотят остановиться в этом бесконечном отеле.Но самое интересное: число жителей её планеты Р-616 не является конечным.Оно бесконечно.
Здесь логика перемещения (N + бесконечность) не применима. Но в таком случае каково же будет решение?
Давайте не складывать, а умножать. На 2. Постоялец первого номера переместится во второй номер, постоялец второго — в четвёртый, третьего — в шестой. В общем случае постоялец номера N переместится в номер (2 * N). Заметили закономерность? Все чётные номера заселяются теми, кто уже являются постояльцами отеля, а все нечётные номера освобождаются для вновь прибывающих. И таким образом, все нечётные номера (число которых бесконечно) могут быть заняты новыми, вновь прибывшими посетителями, число которых также бесконечно.
Преодолевая все ограничения O(INFINITE of INFINITE)
Всем жителям планеты Р-616 очень понравилось их пребывание в бесконечном отеле.Они стали публиковать в соцсетях фото и видео, которые мгновенно становились вирусными. Больше месяца хештег #stay_at_infinite_hotel был № 1 по популярности в твиттере.В отель прилетало всё больше и больше народу.И если вы думаете, что теперь никаких проблем возникнуть не может, то вы ошибаетесь.
На межвселенских галактических переговорах был принят закон, согласно которому все жители всех планет в назначенную дату одновременно должны заселиться в этот отель.Чтобы вы понимали: количество этих планет бесконечно, и число жителей каждой из них бесконечно,и все хотят остановиться в отеле одновременно.Как же их всех разместить?
Мы не можем здесь проделать предыдущий трюк: нечётно-чётная стратегия применима лишь в случае одной планеты с бесконечным числом жителей. А как быть с другими планетами? Подумайте немного об этом, прежде чем идти дальше. Ну хорошо, дам подсказку: согласно теореме Евклида существует бесконечно много простых чисел.
Итак, давайте возьмём первое простое число 2. Теперь переместим постояльцев в их новые номера. Для этого число 2 возводим в степень, соответствующую занимаемому ими номеру. Так постоялец первого номера переместится в номер 2¹. Постоялец второго номера переместится в номер 2². Постоялец третьего номера переместится в номер 2³. В общем случае постоялец номера N перемещается в номер 2^N. А как насчёт первой планеты с бесконечным числом жителей? Возьмём число 3 и будем возводить его в степень, соответствующую порядковому номеру каждого прибывающего с этой планеты, и таким образом предоставим им всем номера. Первому — номер 3¹, второму — номер 3² и т. д. Так, P-й прибывший будет заселён в номер 3^P. Эта же логика будет применяться и в отношении прибывающих со всех остальных планет, то есть 5^P, 7^P, 11^P, 13^P и т. д. Теперь, когда каждому постояльцу соответствует его степень простого числа, все постояльцы будут размещены каждый в отдельном номере! Так что у нас есть способ принять бесконечное количество прибывающих с бесконечного количества планет — infinite of infinite!
ЭПИЛОГ
Приём в «Гранд-отеле» имел грандиозный успех!Всем очень понравилось отдохнуть в нём.Это был праздник галактического масштаба,который теперь будут отмечать ежегодно.
«Да будет свободный номер. И свободный номер появился!». (Управляющий бесконечного «Гранд-отеля»).
И в следующий раз, когда вам понадобится номер в отеле, загляните в этот бесконечный отель. Здесь для вас всегда найдётся свободный номер. Разве что ближе к вечеру, возможно, придётся переместиться в один из соседних номеров. 😉
Спасибо, что дочитали. А вы хотели бы остановиться в этом бесконечном отеле?
Источник
Проект Байхоу
Каждый может измениться
Парадокс «Гранд-отель» или парадокс бесконечного отеля
Grand Hotel Paradox
В 1920-е годы немецкий математик Дэвид Гильберт придумал известный мысленный эксперимент, чтобы показать, как сложно осознать концепцию бесконечности. Представьте отель с бесконечным количеством комнат и очень трудолюбивым ночным менеджером. Как-то ночью Бесконечный отель оказался полностью заполнен — всё было занято бесконечным количеством гостей. В отель входит мужчина и просит комнату. Вместо отказа ночной менеджер решает освободить для него комнату. Как? Просто. Он просит гостя из комнаты No1 переместиться в комнату No2, гостя из комнаты No2 — в комнату No3 и так далее. Каждый гость переезжает из комнаты n в комнату n+1. Поскольку количество комнат бесконечно, для каждого постояльца найдётся новая комната. А первая комната освободится для нового клиента.
Действия могут повторяться для любого конечного числа новых гостей. Если, скажем, туристический автобус привезёт 40 человек для размещения, тогда каждый постоялец просто переедет из комнаты n в комнату n+40, таким образом освобождая первые 40 комнат.
Теперь приезжает бесконечно большой автобус со счётным бесконечным количеством пассажиров, желающих снять комнаты. «Счётное бесконечное» — ключевое понятие. Автобус с бесконечным количеством пассажиров сначала сбивает с толку менеджера, но он находит способ разместить новых гостей. Он просит гостя из комнаты No 1 перейти во комнату No 2. Потом он просит гостя из комнаты No 2 переместиться в комнату No 4, гостя из комнаты No 3 — в комнату No 6 и так далее. Каждый постоялец переезжает из комнаты n в комнату 2n, заполняя только бесконечное количество чётных комнат. Таким образом, он освободил бесконечное количество нечётных номеров, которые потом занимают пассажиры бесконечного автобуса.
Все счастливы и гостиничный бизнес процветает лучше, чем когда-либо. Вообще, он процветает так же, как и всегда, принося бесконечное количество долларов за ночь. О потрясающем отеле разносятся слухи. Люди съезжаются отовсюду. Как-то ночью происходит невообразимое. Ночной менеджер смотрит на улицу и видит нескончаемую череду бесконечно больших автобусов со счётным бесконечным количеством пассажиров. Что же ему делать? Если он не найдёт для них комнат, отель понесёт бесконечные убытки, и он точно лишится работы. К счастью, он вспоминает, что примерно в 300 году до нашей эры Евклид доказал существование бесконечного количества простых чисел.
Чтобы выполнить, казалось бы, невозможное — найти бесконечные кровати для бесконечных автобусов с бесконечно усталыми путешественниками — ночной менеджер определяет каждого постояльца в комнату с номером первого простого числа — 2, возведённым в степень, равную номеру их настоящей комнаты. Так, постоялец из седьмой комнаты переходит в комнату 2 7 (два в седьмой степени), то есть в комнату No 128.
Пассажиры второго автобуса определяются в комнаты со степенями следующего простого числа — 5. Следующий автобус — со степенями 7. Каждый следующий автобус — со степенями 11, степенями 13, степенями 17 и так далее.
Так как в каждом таком числе только единица и степень с натуральным показателем простого числа могут быть множителями, то номерá комнат не совпадают. Все пассажиры автобусов распределяются по комнатам с помощью уникальной схемы определения комнат, основанной на уникальных простых числах. Так ночной менеджер может расселить каждого пассажира из каждого автобуса. Хотя останется множество незанятых комнат, таких как шестой номер, поскольку 6 не является степенью простого числа. К счастью, начальники не так хороши в математике, поэтому его должность в безопасности.
Схемы ночного менеджера возможны только потому, что хотя Бесконечный отель похож на логистический кошмар, он сталкивается с наименьшим уровнем бесконечности, главным образом со счётным бесконечным множеством натуральных чисел — 1, 2, 3, 4 и так далее. Георг Кантор назвал этот уровень бесконечности алеф-нуль. Мы используем натуральные числа для комнат и для номеров мест в автобусах. Используя высшие порядки бесконечности, такие как действительные числа, эти упорядоченные схемы были бы невозможны, потому что нельзя было бы всегда включать каждое число.
Бесконечный отель действительных чисел имеет «отрицательные» комнаты в подвале, дробные комнаты, поэтому мужчина в комнате No 1/2 подозревает, что него комната меньше, чем у гостя в комнате No 1. Комнаты квадратного корня, например, комната корня из двух, и комната Пи, где гости ожидают бесплатный пирог. Какой уважающий себя ночной менеджер вообще захочет там работать, даже за бесконечную зарплату? Но в Бесконечном отеле Гильберта, где никогда нет свободных мест, но всегда есть ещё одно — ситуации, с которыми сталкивается добросовестный и, возможно, слишком радушный менеджер, напоминают нам, как сложно нашим относительно ограниченным умам осознать такое огромное понятие, как бесконечность. Может, вы поможете решить эти проблемы после хорошего ночного сна. Но, если честно, нам может понадобиться поменять комнаты в 2 часа ночи.
Источник
Концепция бесконечности, возможно, одна из самых изящных и смелых концепций, когда-либо созданных человечеством. Однако еще со времен Древней Греции бесконечность не только завораживала, но и откровенно раздражала ученых и философов: она предполагала слишком много парадоксов, идущих вразрез со всякой логикой. Рассказывая о теории чисел и теории множеств, математик Хаим Шапира сосредоточил свое внимание на бесконечности, к которой каждая из этих теорий напрямую относится, и не без успеха попытался примирить многочисленные парадоксы с нашей картиной мира. Валерий Шлыков изучил его книгу в рамках совместного проекта «Горького» и премии «Просветитель» и выбрал из нее несколько наиболее важных и интересных эпизодов.
Хаим Шапира. Восемь этюдов о бесконечности. Математическое приключение. М.: КоЛибри, Азбука-Аттикус, 2021. Перевод с английского Дмитрия Прокофьева. Содержание
 Бесконечность — это иррационально
Бесконечность — это иррационально
Удивительно, но человечество далеко не сразу пришло к пониманию иррациональной сути бесконечности. Мы привыкли, что рациональность — это наивысшая степень ясности и логичности, нечто, присущее прежде всего строго разработанной науке, однако первобытные мифы обладали не менее четкой логикой. Понадобился гений древних греков, чтобы нехотя, со скандалом, но признать не укладывающуюся ни в какую логику бесконечность. Считается, что первым ее ввел в философский обиход Анаксимандр, автор концепции апейрона, хотя апейрон у него обозначал скорее неопределенность. Такая бесконечность особых возражений еще не вызвала. А вот Пифагору открылось нечто совершенно возмутительное. Пифагор-философ считал, что все состоит из натуральных (то есть положительных целых) чисел и ими может быть выражено. Числа были атомами его мира. А Пифагор-математик обнаружил, что соотношение между стороной квадрата и его диагональю невозможно выразить отношением натуральных чисел. Иными словами, √2 — иррациональное число (напомним: иррациональность числа подразумевает, что, во-первых, его десятичное представление бесконечно, а во-вторых, в нем никогда не возникают какие бы то ни было повторяющиеся структуры).
Джин из бутылки был выпущен. Две тысячи лет спустя Георг Кантор показал, что «почти» все вещественные (или действительные) числа иррациональны. Среди них и два самых важных числа в математике — число Эйлера и отношение длины окружности к ее диаметру, число п.
Кстати, когда в 1593 году французский математик Франсуа Виет нашел замечательную формулу для вычисления π при помощи набора вложенных радикалов, он записал ее в следующем виде:
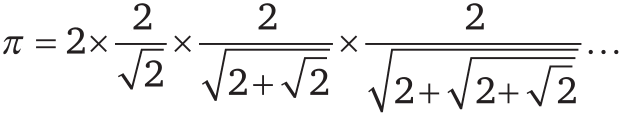 Стоящее в конце многоточие означает «продолжать ту же процедуру до бесконечности». Это первый случай, когда бесконечный процесс был явно обозначен в математической формуле. Ну а знаменитый знак бесконечности ∞ впервые использовал английский математик Джон Валлис в 1655 году.
Стоящее в конце многоточие означает «продолжать ту же процедуру до бесконечности». Это первый случай, когда бесконечный процесс был явно обозначен в математической формуле. Ну а знаменитый знак бесконечности ∞ впервые использовал английский математик Джон Валлис в 1655 году.
Бесконечность — это парадоксально
Вернемся к грекам. По-настоящему скандал с бесконечностью раздул Зенон Элейский, ученик Парменида. С тех пор его знаменитые апории обсуждались бесчисленное количество раз. Рассел называл их «неизмеримо тонкими и глубокими», а Пуанкаре, напротив, эмоционально заявлял, что «Зенон был идиотом, и только идиоты могут заниматься его апориями».
До нас дошли девять апорий, но наиболее известны из них три. «Стрела» — о стреле, которая в каждый момент времени покоится, а значит, никуда не летит. «Дихотомия», в которой идущий из точки A в точку B никогда туда не доберется, так как ему сначала нужно пройти половину этого расстояния, а затем половину оставшегося расстояния и так далее, так что до точки B всегда будет оставаться еще какая-то крошечная половинка. И, конечно же, «Ахиллес и черепаха» — в которой Ахиллес никогда не догонит черепаху, если та пустилась в путь немного раньше, так как всякий раз, как Ахиллес прибывает на то место, где только что была черепаха, та успевает продвинуться хоть чуть-чуть, но дальше.
Рассуждения Зенона безупречны, однако допустить в реальности, чтобы бегун не перегнал какое-то пресмыкающееся, попросту нелепо. Так была найдена парадоксальная сторона бесконечности, которая противоречит всему нашему опыту. Изящным математическим выражением этой парадоксальности служит простое уравнение 1=0,999999… Здесь всякий поначалу заподозрит какой-то подвох. Нет, тут не может быть знака равенства: пусть на ничтожную величину, но правая часть формулы все-таки должна быть меньше единицы! Однако доказательство элементарно и безжалостно. Пусть a=0,9999999… В таком случае 10a=9,999999… Вычтя одно число из другого, получим 10a — a = 9,999999… — 0,999999… Что дает 9a=9, то есть a=1.
В бесконечности — значит нигде
Еще одна парадоксальная характеристика заключается в том, что, по формулировке Гегеля, «бесконечность нельзя найти ни в одной точке бесконечной прямой». Представим себе космический корабль, который движется по следующим правилам: первые полчаса он летит со скоростью 2 километра в час (или 2 тысячи, или 2 миллиона, что совершенно неважно). На следующую четверть часа его скорость несколько возрастает — до 4 километров в час. В течение следующей одной восьмой часа он летит со скоростью 8 километров в час — и так далее. Где этот космический корабль окажется через час? Цифры подобраны таким образом, чтобы получить несложный расчет: за первые полчаса он пролетит километр, за следующие четверть часа — еще километр, и так далее, то есть в итоге он преодолеет расстояние 1+1+1+1… Но поскольку это число бесконечно, мы не можем указать ни одну точку в космосе, где бы мог оказаться корабль, ведь до любой точки будет пусть сколько угодно большое, но конечное расстояние. Корабль попросту нигде, он исчез из нашего вычислимого мира. Словно бы перешел на иной уровень существования.
Бесконечность — это красиво
Греков бесконечность пугала. Она была чем-то вроде вторжения хаоса в их упорядоченный и размеренный космос. Однако вскоре обнаружилось, что бесконечность обладает своей завораживающей красотой, своей «рациональностью». Эта красота, например, очевидна в приведенной выше формуле Виета для вычисления π. А вот еще одна невероятная красота:
1/9801 = 0,0001020304050607080910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758…
Для наглядности напишем это число с пробелами:
1/9801 = 0,00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 99 00 01 02 03… 97 99 00 01 02 03 04 05 06…
Мы получили все двузначные числа, расположенные в правильном порядке и повторяющиеся до бесконечности, кроме числа 98! По сравнению с подобным меркнет вся красота конечного мира, ведь здесь мы прикасаемся к чему-то запредельному и как бы божественному — к той гармонии, которая, возможно, лежит в основе всего (а теперь попробуйте самостоятельно поделить 1 на 998 001).
Бесконечность — это божественно
В 1913 году профессор математики Кембриджского университета Годфри Харди получил письмо из Индии от никому не известного индийского юноши, закончившего только среднюю школу. В письме было несколько уравнений, потрясших Харди. Например:
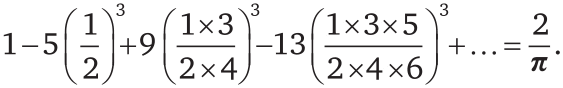 Так мир узнал о Рамануджане. Он был гениальным самоучкой и поддерживал с числами какие-то мистические отношения. Иначе невозможно объяснить, как Рамануджан открывал свои формулы.
Так мир узнал о Рамануджане. Он был гениальным самоучкой и поддерживал с числами какие-то мистические отношения. Иначе невозможно объяснить, как Рамануджан открывал свои формулы.
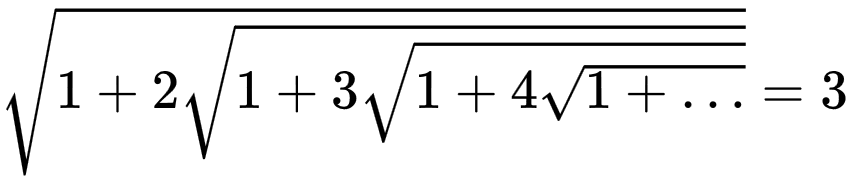 Многие сравнивали их с симфониями Моцарта или картинами эпохи Возрождения, но сам Рамануджан утверждал, что они внушались ему во время сна или медитации богиней Махалакшми. Как знать, не боги ли поспешили забрать к себе индийского гения (Рамануджан умер в 32 года), ведь он и так выдал немало их секретов. Подобных формул он успел записать более 3 900!
Многие сравнивали их с симфониями Моцарта или картинами эпохи Возрождения, но сам Рамануджан утверждал, что они внушались ему во время сна или медитации богиней Махалакшми. Как знать, не боги ли поспешили забрать к себе индийского гения (Рамануджан умер в 32 года), ведь он и так выдал немало их секретов. Подобных формул он успел записать более 3 900!
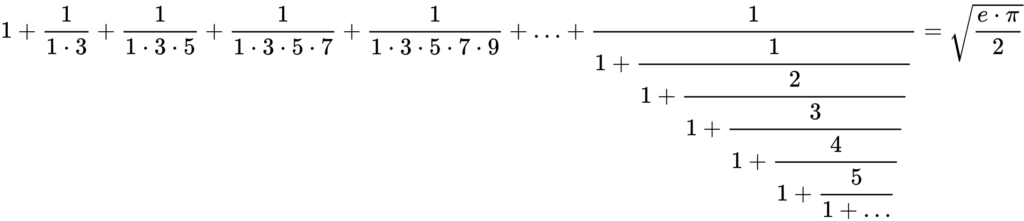
Брадобрей уделывает Кантора
Еще одним человеком, состоявшим с бесконечностью в чрезвычайно близких отношениях, был Георг Кантор, наш соотечественник (он родился в Санкт-Петербурге в 1845 году). Ему принадлежит разработка теории множеств, которая стала прорывом в математике. До него считалось, что «бесконечность распознаваема, но не познаваема» (Декарт). В лучшем случае бесконечность оценивали «на глазок», как, например, Эйлер, полагавший, что бесконечность 2/0 вдвое больше, чем 1/0. Кантор математически показал, что бесконечные множества (как и конечные) можно сравнивать, производить над ними операции, формулировать и доказывать теоремы с ними. Однако и здесь сразу же вмешались парадоксы — куда без них в бесконечности?
Когда Готлоб Фреге уже заканчивал фундаментальный двухтомный труд «Основные законы арифметики», в основу которого были положены выкладки Кантора, он получил письмо от Бертрана Рассела, заставившее его посыпать голову пеплом. В этом письме Рассел вывел свой знаменитый парадокс брадобрея, который бреет всех, кто не бреется сам. За софистическим с виду содержимым скрывалась серьезная проблема.
В теории Кантора множество — это совокупность каких-то объектов. Если среди этих объектов нет самого множества, такое множество считалось обычным. Например, множество всех кроликов само кроликом не является. Но множество не-кроликов уже «необычно» — ведь оно тоже «не-кролик», значит, входит в самого себя. Такое множество стали называть расселовским. Парадокс возникает, когда рассматривается множество всех обычных множеств, которое оказывается не обычным, не расселовским. Оно не обычное, так как, будучи обычным множеством, должно входить в самого себя, то есть на самом деле быть расселовским множеством. И оно не расселовское, так как, если оно входит в самого себя в качестве расселовского, это противоречит его определению как множеству только обычных множеств. Таким образом, оказалось, что разделение множеств на те, что не являются собственными элементами, и те, что являются таковыми, не исчерпывает всех множеств. Есть еще и «брадобреи».
Гранд-отель «Бесконечность» имени Гильберта: свободные номера есть всегда!
Немецкий математик Давид Гильберт придумал, пожалуй, самый изящный пример, связанный с парадоксами бесконечности. Представим себе отель с бесконечным количеством номеров, в котором живут постояльцы — все натуральные числа: 1, 2, 3, 4… Свободных номеров, естественно, нет, что вполне устраивает портье. Но вот в гостиницу пожаловал важный гость: 0. Можно ли его разместить? Сообразительный портье попросил каждого из жильцов переехать в следующий по порядку номер, освободив тем самым для ноля № 1. Лиха беда начало. Стало известно, что в отеле все-таки могут быть свободные номера, и первыми подсуетились все отрицательные числа, которых, понятно, тоже бесконечность. Прежний способ не работает: нельзя попросить постояльцев переехать на бесконечное число номеров. Однако можно переселить каждого жильца в номер с удвоенным значением: 2 в № 4, 3 в № 6 и так далее. Тогда все нечетные номера (3, 5, 7, 9…) освободятся и получится бесконечное количество незанятых комнат.
Слава о гостинице, в которой всегда есть свободные номера, растет, и теперь сюда желают пожаловать все положительные рациональные дроби. Портье с ужасом осознает, что прежний метод опять бесполезен: ведь одни только числа со знаменателем 2 могут полностью занять отель, если дробь ½ поселится в № 1, дробь 2/2 — в № 2, дробь 3/2 — в № 3 и так далее. А таких знаменателей бесконечность! То есть нужно разместить бесконечное количество бесконечных множеств. Тем не менее наш портье блестяще справился с этой задачей, оставив про запас еще одну бесконечность номеров. Как? Прочитайте в книге или посмотрите наглядный ролик.
Гранд-отель «Бесконечность» имени Гильберта: трест, который лопнул
Итак, в гостиницу постоянно и без проблем въезжают разные бесконечности и даже бесконечности бесконечностей. Поэтому портье и глазом не моргнул, когда к стойке регистрации подошло скромное множество всех чисел между 0 и 1. Конечно, в этом интервале тоже содержится бесконечное количество, но разве не в этом специализация нашего отеля? Однако все попытки перемножать, возводить в степень и прочие манипуляции с номерами ни к чему не привели: числа между 0 и 1 в отель не влезали. В отчаянье портье даже выселил всех постояльцев, но и пустая гостиница не могла вместить в себя не то что все числа между 0 и 1, но даже дроби, записанные с использованием только цифр 0 и 1, то есть 0,101 и так далее. Репутация отеля обвалилась, поползли слухи, что гранд-отель «Бесконечность» на самом деле маленький. Торжествующие конкуренты немедленно открыли рядом «Еще большую бесконечность». Но как такое возможно?
«Вижу, но не верю!»
Мы уже упоминали, что именно Кантор научился сравнивать бесконечные множества. Оказалось, что счетные множества (элементы которых можно пронумеровать натуральными числами) — это самые простые или «маленькие» множества. Их мощность (то есть количество элементов) обозначается буквой еврейского алфавита ℵ0 («алеф-нуль»). Мощность несчетных (состоящих из вещественных чисел) множеств больше и обозначается как ℵ. Равна ли она ℵ1, математики спорят до сих пор, однако несомненно, что есть множества с мощностью ℵ2, ℵ3 и так далее.
Мы видели, что даже простые счетные множества очень интересны, так как позволяют включать в себя разные бесконечности. Обладают ли таким свойством несчетные множества? Конечно! Их еще называют континуум-множествами, так как геометрически их можно представить в виде непрерывных отрезков или линий. При этом любые два отрезка равномощны, то есть имеют равное (хоть и несчетное) количество своих точек. Доказательство легко видно из рисунка:
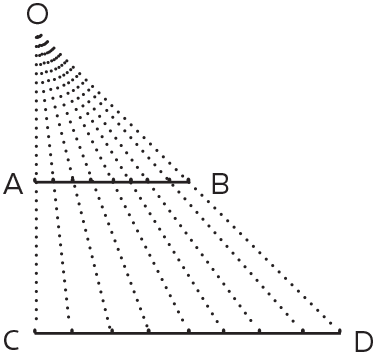 С этим еще можно согласиться, но как вам равномощность любого конечного отрезка и бесконечного луча? Однако она становится очевидной, если провести те же линии соответствия на следующем рисунке:
С этим еще можно согласиться, но как вам равномощность любого конечного отрезка и бесконечного луча? Однако она становится очевидной, если провести те же линии соответствия на следующем рисунке:
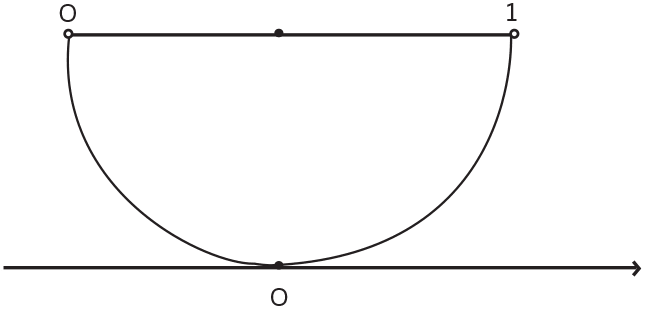 И уж совсем невероятна равномощность бесконечной прямой и n-мерного пространства (для любого n!). Говорят, когда Кантор доказал это, он воскликнул: «Je le vois, mais je ne le crois pas!» («Вижу, но не верю!»)
И уж совсем невероятна равномощность бесконечной прямой и n-мерного пространства (для любого n!). Говорят, когда Кантор доказал это, он воскликнул: «Je le vois, mais je ne le crois pas!» («Вижу, но не верю!»)
Бесконечность — это трансцендентно
Теория счетных и несчетных множеств позволяет проникнуть в совсем уже запредельную тайну бесконечности. Как мы писали, все действительные числа можно разделить на рациональные и иррациональные. Однако в математике куда важнее другое разделение: на алгебраические и трансцендентные. Число называется алгебраическим, если оно является корнем какого-либо многочлена с целыми коэффициентами (простейший пример: bx — a). Любое рациональное число будет решением подобного многочлена, как и некоторые иррациональные числа: например, √2 является корнем уравнения x2 — 2 = 0. Характеристика алгебраичности очень важна, так как все алгебраические числа образуют счетное множество, внутри которого возможны четыре основных алгебраических действия: сложение, вычитание, умножение, деление (разумеется, кроме деления на 0).
А что же с неалгебраическими числами, то есть теми, которые невозможно представить в виде корней многочленов и которые образуют несчетное множество? Долгое время их попросту не могли найти! И только в 1844 году французский математик Жозеф Лиувилль открыл первое трансцендентное число. Вот оно:
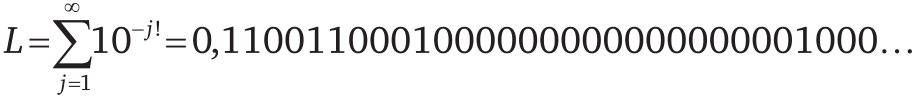 Строится оно следующим образом. Сначала вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120… Затем составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1, 2, 6, 24, 120-м — и так далее — местах, а на всех остальных местах стоит 0. Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.
Строится оно следующим образом. Сначала вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120… Затем составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1, 2, 6, 24, 120-м — и так далее — местах, а на всех остальных местах стоит 0. Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.
Можно подумать, такое число — редкий зверь в числовом зверинце, но ничего подобного! Кантор обнаружил, что трансцендентные числа составляют большинство всех чисел. Другими словами, практически все числа не только не рациональны, по большей части они даже не относятся к алгебраическим!
Но где же тогда все эти трансцендентные числа? Видимо, где и должны быть: в трансцендентной бесконечности. Лишь некоторые нам удается изловить оттуда, изощренно доказывая, что они не являются алгебраическими. Так, трансцендентность числа π была доказана лишь в 1882 году, трансцендентность постоянной Гельфонда eπ — в 1934-м, а десятичный логарифм ln π до сих пор ждет решения своей судьбы. Бесконечность неохотно раскрывает свои тайны, коих у нее, без сомнения, бесконечное множество.
| Эту задачу предложил немецкий математик Давид Гильберт где то в третьем десятилетии 20 века. Давид был одним из величайших умов своего времени. Среди большого числа его учеников, которые в последствии стали видными учеными, был Джон Фон Нейман. Он так же консультировал Эйнштейна при разработке тензорного анализа — фундамента теории относительности. |  |
Один гость
Напомню вам условие задачи для одного гостя из предыдущей статьи:
Представьте себе гостиницу с бесконечным числом комнат. Комнаты пронумерованы натуральными числами, от 1 до ∞. В один прекрасный день в нашу гостиницу вошел человек и попросил снять комнату. К сожалению, для нашего гостя не нашлось комнаты, так как именно в этот день отель был полностью заполнен бесконечным числом гостей. Выгнать гостя? Или все же есть возможность предоставить ему свободную комнату не выселяя никого из постояльцев?
Несмотря на то, что задача явно говорит что все номера заняты, мы все же можем выделить сколько угодно свободных комнат. Давайте просто переселим человека из первой комнату во вторую, человека из второй комнаты в третью и так далее. То есть, каждого гостя из комнаты с номером n переселим в комнату с номером n+1, n→n+1. В результате этого у нас освобождается комната с номером один, и мы с радостью можем поселить нашего нового гостя.
Бесконечное число гостей
Напомню условие:
Если вы смогли найти комнату для одного гостя значит вы замечательный администратор. Но всегда есть простор для улучшения ваших навыков. Представьте что в полностью заполненный бесконечный отель приехало бесконечное число гостей. Как бы вы поселили бесконечное число гостей, при этом не выселяя никого из бесконечного числа постояльцев?
Задача стала интереснее. Может ли бесконечность вместить еще одну бесконечность? Для решения предыдущей задачи мы переселили каждого гостя на один номер вперед. Этот подход можно применить для любого конечного числа постояльцев. Если n номер комнаты постояльца, а m число прибывших гостей, тогда каждого постояльца надо переселить в номер n+m, чтобы освободить m номеров для m гостей. Но что если число гостей бесконечно, то есть m=∞?. Чему равно n+∞? Давайте попросим «Вольфрам Альфа» дать нам ответ: n+∞=∞. То есть, надо переселить каждого постояльца на ∞ номеров. Нет, это нам не подходит. Но задача имеет решение, давайте взглянем на определение четного числа:
Четное число — целое число, которое делится без остатка на 2.
Что если мы возьмем номер постояльца и умножим его на два? В результате мы получим четное число, так как оно будет делится на два. Следовательно если мы переселим каждого гостя из номера n в номер 2×n, n→2×n, мы получим бесконечное число нечетных свободных комнат, и мы сможем поселить бесконечное число гостей. Только не спрашивайте сколько времени займет переселения гостя из комнаты номер 8140406085191601 в комнату номер 16280812170383202.
***
Этот парадокс хорош тем, что он отлично показывает странные, но вполне логичные свойства бесконечности в простых и понятных сущностях. Посмотрите так же этот интересный ролик: