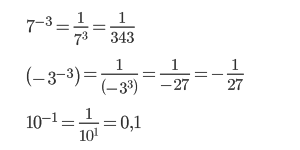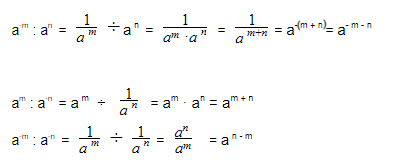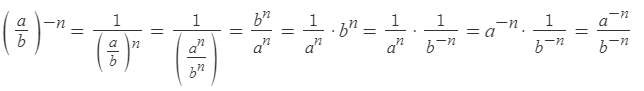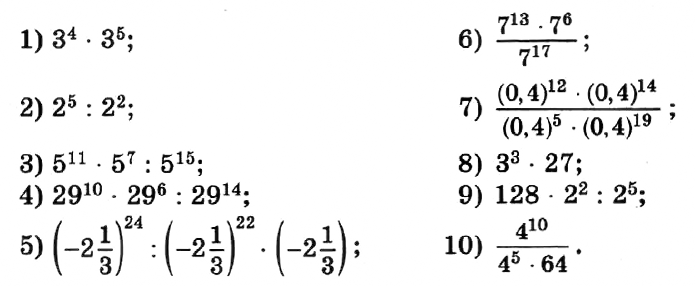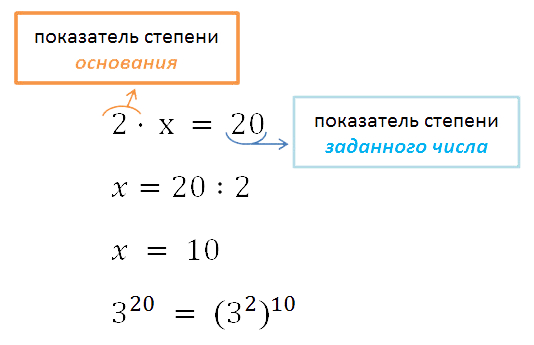Что такое степень числа
В учебниках по математике можно встретить такое определение:
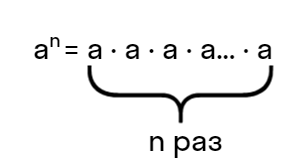
«Степенью n числа а является произведение множителей величиной а n раз подряд»
- an — степень,
где:
a — основание степени;
n — показатель степени.
Соответственно:
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
- 23 = 2·2·2, где:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
- 3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.
Математики заскучали и решили все упростить:
- 34 = 81
Ответ: через четыре года у вас будет 81 миллион.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).
| Число | Вторая степень | Третья степень |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Свойства степеней
В математике степень с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Мы будем употреблять такие понятия, как натуральные числа, целые числа, рациональные числа, иррациональные числа. Чтобы не запутаться, дадим им определение:
- Натуральные числа — это числа, которые мы используем, чтобы считать предметы: один банан, два банана.
- Целые числа — это все натуральные числа, все противоположные натуральным числам и число 0.
- Рациональными называют числа, которые можно представить в виде обыкновенной дроби. Например: 1/2; −5/3; 8/4.
- Иррациональные числа — это бесконечная десятичная дробь. Например, число пи как раз такое — 3,141592…
Все, теперь мы точно готовы разбираться со свойствами степеней. Поехали!
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
an · am = am+n
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в степень
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
(an)m = an· m
a — основание степени
m, n — показатели степени, натуральное число
Свойство 4: возведение в степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b)n = an · bn
a, b — основание степени
n — показатели степени, натуральное число
Свойство 5: возведение в степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b)n = an : bn
a, b — основание степени, b ≠ 0,
n — показатель степени, натуральное число
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
23+ 34= 8 + 81= 89
63— 33= 216 — 27 = 189
И еще парочка правил
- Если есть скобки — начинать вычисления нужно внутри них
- Только потом возводим этот результат из скобок в степень
- Затем выполняем остальные действия: сначала умножение и деление по порядку (слева направо), а в конце — сложение и вычитание по порядку (слева направо)
Давай потренируемся
Реши примеры со степенями:
-
23 + 24 =
-
34 + 54 =
-
63 − 33 =
-
74 − 32 =
В конце статьи ты найдешь правильные ответы.
Примеры умножения и деления степеней
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, можно перемножить основания и возвести произведение в степень, показатель которой останется прежним:
- an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35 + 2 = 37 = 2 187
- 28 · 81= 28 · 23 = 28 + 3 = 211 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
- 33 · 52 = 27·25 = 675
Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- an : bn = (a : b)n , где
a, b — основание степени, b ≠ 0,
n — показатель степени, натуральное число
Пример:
53 : 23 = (5 : 2)3 = 2,53 = 15,625
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
- 33 ÷52 = 27÷25 = 1,08
Степень с отрицательным показателем и её свойства
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Примеры
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
- a3÷a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
am · an = am+n
Примеры
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Примеры
Возведение дроби в отрицательную степень
Возведение произведения в отрицательную степень
Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
243 = 3 × 3 × 3 × 3 × 3 = 35
Ответы на вопросы для самопроверки
-
24
-
706
-
189
-
2392
Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.
Калькулятор степеней
Возвести в степень
Возведений в степень:
Что такое натуральная степень числа?
Число p называют n-ой степенью числа a, если p равно числу a, умноженному само на себя n раз: p = an = a·...·a
n — называется показателем степени, а число a — основанием степени.
Как возвести число в натуральную степень?
Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:
Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 34
Решение: как было сказано выше, 34 = 3·3·3·3 = 81.
Ответ: 34 = 81.
Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 55
Решение: аналогично, 55 = 5·5·5·5·5 = 3125.
Ответ: 55 = 3125.
Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.
Что такое отрицательная степень числа?
Отрицательная степень -n числа a — это единица, поделённая на a в степени n: a-n =
.
При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.
Как возвести число в целую отрицательную степень?
Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.
Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2-4
Решение: как было сказано выше, 2-4 = = = 0.0625.
Ответ: 2-4 = 0.0625.
При помощи нашего калькулятора вы легко сможете возвести число в любую степень.
Что же такое возведение числа в степень? Для того, что бы это понять давайте с вами разберем простой пример:
43
из которых 4 — это основание, 3 – степень в которую необходимо возвести основание.
Решение данной задачи состоит в следующем
4*4*4 = 64.
Таким образом мы можем сделать простой вывод возведение числа в степень это умножение этого числа на само себя столько раз в какой степени он находиться.
Возводить можно не только в положительную степень, но и в отрицательную. Многие задаются вопросом как возвести в отрицательную степень. При возведении в отрицательную степень надо как обычно возвести число в степень и разделить на него единицу.
Таким образом выражение
4-3
Записывается следующим образом
1/(4*4*4)= 1/64 = 0,015625
Таблица степеней 8 представлена ниже.
Степени числа 8
Степени 8 от 0 до 10 помогут вам в расчетах.
Таблица:
| Степени 8 | Результат | |
| 8 в 0 степени | 80 | 1 |
| 8 в 1 степени | 81 | 8 |
| 8 в 2 степени | 82 | 64 |
| 8 в 3 степени | 83 | 512 |
| 8 в 4 степени | 84 | 4096 |
| 8 в 5 степени | 85 | 32768 |
| 8 в 6 степени | 86 | 262144 |
| 8 в 7 степени | 87 | 2097152 |
| 8 в 8 степени | 88 | 16777216 |
| 8 в 9 степени | 89 | 134217728 |
| 8 в 10 степени | 810 | 1073741824 |
Степень Таблица степеней Школьная алгебра Школьная геометрия
С этим удобным калькулятором вы можете производить операции по возведению в степень.
3x2=
2xy4=
510X=
Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.
Калькулятор степеней
С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».
Таблица степеней от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
| 11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625 |
| 61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Теория
Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется — основанием степени, а количество операций умножения — показателем степени.
an = a×a … ×a
запись читается: «a» в степени «n».
«a» — основание степени
«n» — показатель степени
Пример:
46 = 4 × 4 × 4 × 4 × 4 × 4 = 4096
Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.
Скачать таблицу степеней
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
УчебаМатематика
Возведение в произвольную степень, извлечение корня произвольной степени.
Калькулятор создан по запросу пользователя. Введенное число возводит в указанную степень и извлекает корень указанной степени.
![]()
Корень и степень
Точность вычисления
Знаков после запятой: 4
Степень
Корень
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Решение уравнения 4-й степени
- • Математический калькулятор
- • Производная показательно-степенной функции
- • Вычисление корней полинома
- • Возведение полинома в степень
- • Раздел: Математика ( 245 калькуляторов )
#математика #уроки корень Математика степень
PLANETCALC, Корень и степень
Timur2020-11-03 14:19:28
Вычислить : 5(в 8 степени ) * 5( — 4.
Степени) : 5(3 степени).
Перед вами страница с вопросом Вычислить : 5(в 8 степени ) * 5( — 4?, который относится к
категории Алгебра. Уровень сложности соответствует учебной программе для
учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Таблица степеней является незаменимым помощником, когда нужно возвести натуральное число в пределах 10 в степень, превышающую два. Достаточно открыть таблицу и найти число, находящееся напротив нужного основания степени и в столбце с нужной степенью – оно и будет ответом на пример. Кроме удобной таблицы, внизу страницы приведены примеры возведения в степень натуральных чисел до 10. Выбрав необходимый столбец со степенями нужного числа, можно легко и просто найти решение, так как все степени расположены в порядке возрастания.
Важный нюанс! В таблицах не представлено возведение в нулевую степень, поскольку любое число в степени ноль равно единице:
a0=1
Задание №8 ОГЭ по математике проверяет у ученика умение преобразовывать и вычислять выражения со степенями.
Для верного решения задания №8 необходимо:
- знать: натуральные числа, обыкновенные и десятичные дроби;
- знать основные свойства степеней и уметь выполнять основные действия со степенями с целыми показателями;
- знать наибольший общий делитель и наименьшее общее кратное;
- знать основное свойство дроби;
- знать числовые выражения, порядок действий в них, использование скобок.
Свойства степеней:$$textcolor{coral}{a}^textcolor{coral}{m}cdottextcolor{coral}{a}^textcolor{darkgreen}{n}=textcolor{coral}{a}^{textcolor{coral}{m}+textcolor{darkgreen}{n}}$$$$textcolor{coral}{a}^textcolor{coral}{m}:textcolor{coral}{a}^textcolor{darkgreen}{n}=textcolor{coral}{a}^{textcolor{coral}{m}-textcolor{darkgreen}{n}}$$$$textcolor{coral}{a}^textcolor{darkgreen}{n}cdottextcolor{blue}{b}^textcolor{darkgreen}{n}={(textcolor{coral}{a}cdottextcolor{blue}{b})}^{textcolor{darkgreen}{n}}$$$$textcolor{coral}{a}^textcolor{darkgreen}{n}:textcolor{blue}{b}^textcolor{darkgreen}{n}={(textcolor{coral}{a}:textcolor{blue}{b})}^{textcolor{darkgreen}{n}}$$$${(textcolor{coral}{a}^textcolor{darkgreen}{n})}^textcolor{coral}{m}=textcolor{coral}{a}^{textcolor{darkgreen}{n}cdottextcolor{coral}{m}}$$$$textcolor{coral}{a}^0=1$$$$textcolor{coral}{a}^{textcolor{darkgreen}{-n}}=frac{1}{textcolor{coral}{a}^textcolor{darkgreen}{n}}$$$${(frac{textcolor{coral}{a}}{textcolor{blue}{b}})}^{textcolor{darkgreen}{-n}}={(frac{textcolor{blue}{b}}{textcolor{coral}{a}})}^{textcolor{darkgreen}{n}}$$
Пример №1
$$frac{{5}^{-3}cdot{5}^{14}}{{5}^{9}}$$
Решаем вместе
Скрыть
В числителе применим правило произведения степеней с одинаковыми основаниями.
При произведении степеней с одинаковыми $textcolor{orange}{основаниями}$, $textcolor{orange}{основание}$ переписываем, а $textcolor{blue}{показатели}$ складываем: $${textcolor{orange}{5}}^{textcolor{blue}{-3}}cdot{textcolor{orange}{5}}^{textcolor{blue}{14}}={textcolor{orange}{5}}^{textcolor{blue}{-3+14}}={textcolor{orange}{5}}^{textcolor{blue}{11}}$$
Разделим числитель на знаменатель. Запишем деление в более понятной нам форме: ${5}^{11}:{5}^{9}$
При делении степеней с одинаковыми $textcolor{orange}{основаниями}$, $textcolor{orange}{основание}$ переписываем, а $textcolor{blue}{показатели}$ вычитаем:$${ textcolor{orange}{5}}^{textcolor{blue}{11-9}}={textcolor{orange}{5}}^{textcolor{blue}{2}}=25$$
Ответ: $25$.
Пример №2
$$frac{{({9}^{3})}^{-4}}{{9}^{-14}}$$
Решаем вместе
Скрыть
Пример №3
$$frac{{64}^{2}}{{16}^{3}}$$
Решаем вместе
Скрыть
Пример №4
$${3}^{-7}cdot{({3}^{5})}^{2}$$
Решаем вместе
Скрыть
Пример №5
$$frac{{6}^{12}cdot{11}^{10}}{{66}^{10}}$$
Решаем вместе
Скрыть
Пример №6
$$frac{{(2cdot6)}^{7}}{{2}^{5}cdot{6}^{6}}$$
Решаем вместе
Скрыть
Пример №7
$$frac{{10}^{9}}{{2}^{6}cdot{5}^{8}}$$
Решаем вместе
Скрыть
При выполнении задания 8 ОГЭ по математике необходимо: знать свойства степеней и корней, уметь сравнивать рациональные и иррациональные числа, применять формулы сокращённого умножения.
Пример 1. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 84 2) 2352 3) 4) 252
Решение. Произведение корней равно корню из произведения, т. е. . Тогда
Ответ: 1.
Пример 2. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Ответ: 3.
Пример 3. На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?
В ответе укажите номер правильного варианта.
1) 10,03 2) 10,05 3) 9,96 4) 10,08
Решение. Длина рулона находится в интервале от 10 — 0,05 = 9,95 м до 10 + 0,05 = 10,05 м. Таким образом, только число 10,08 не попадает в этот диапазон.
Ответ: 4.
Пример 4. Сравните числа и 14. В ответе укажите номер правильного варианта.
1) 2) 3)
Решение. Очевидно, что равенство между заданными числами невозможно. Предположим, что справедливо неравенство Возведём обе части неравенства в квадрат и проведём соответствующие преобразования:
Полученное неравенство неверно, а это значит, что предположение неверно. Тогда верно неравенство .
Ответ: 1.
Пример 5. Укажите наименьшее из чисел. В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Сравним сначала первые три числа, представив их в виде корней:
1) 2) 3)
Из этих чисел наименьшим является . Осталось сравнить его с четвёртым значением.
Результат очевиден. Наименьшим оказалось число под номером 4.
Ответ: 4.
Пример 6. Представьте выражение в виде степени с основанием m. В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Используем свойства степеней:
Ответ: 2.
Пример 7. Вычислите . В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Используем свойства степеней:
Ответ: 3.
Пример 8. Какое из чисел является иррациональным? В ответе укажите номер правильного варианта.
1) 2) 3) 4) все числа иррациональны
Решение. Если в результате вычислений или преобразований всё равно остаётся корень, то число является иррациональным:
1) (рациональное число)
2) (иррациональное число)
3) (рациональное число)
Ответ: 2.
Пример 9. Какое из числовых выражений является рациональным? В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Если в результате вычислений корень «исчезнет», то число является рациональным:
1) (иррациональное число)
2) (иррациональное число)
3) (иррациональное число)
4) (рациональное число)
Ответ: 4.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 8 ОГЭ по математике. Числа, вычисления и алгебраические выражения.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.01.2023
Самостоятельная работа № 8 по алгебре в 7 классе «Свойства степени с натуральным показателем» с ответами (Вариант 3). Дидактические материалы (упражнения №№ 54 — 64) для учителей, учащихся и родителей. Алгебра 7 Мерзляк С-08 В3.
№ 54. Представьте в виде степени произведение:
1) n4n6; 4) a6a6; 7) (а + 2b)10(а + 2b);
2) mm7; 5) хх9х4;  у5y2уу11;
у5y2уу11;
3) x2х16; 6) k3k2k8; 9) (у + 6)5(y + 6).
№ 55. Представьте в виде степени частное:
1) а15 : а4; 2) у9 : у; 3) (х – у)12 : (х – y)6.
№ 56. Замените звёздочку такой степенью с основанием а, чтобы выполнялось равенство:
1) а5 • * = а19; 4) * : а10 = а32;
2) а4 • * • a2 = а7; 5) а14 : * • а9 = а11;
3) а9 : * = а5; 6) * • а7 : а23 = а2.
№ 57. Представьте выражение в виде степени и вычислите его значение:
№ 58. Представьте степень в виде произведения степеней:
1) (ху)10; 3) (3у)4; 5) (–0,2kx)4;
2) (mnp)6; 4) (–2xy)6; 6) (3/7 • ab).
№ 59. Представьте в виде степени выражение:
1) x8y8; 3) 36a2b2; 5)–125/216 • m3n3;
2) –n11; 4) 27х3у3; 6) 100 000р5х5.
№ 60. Найдите значение выражения:
1) 0,29 • 59; 3) (1/4)8 • 88; 5) (2 1/3)7 • (3/7)8;
2) 43 • 253; 4) (0,8)4 • (125)4; 6) (0,5)17 • 219.
№ 61. Представьте в виде степени с основанием с выражение:
1) (с3)4; 4) (с5)4; 7) (с8)3 • (с3)8;
2) (–с7)2; 5) ((с2)3)6;  (–с3)5 • (–с5)7 : с25;
(–с3)5 • (–с5)7 : с25;
3) с5с2; 6) (с8)6 : с45; 9) с34 : (с8)2 • с15.
№ 62. Является ли тождеством равенство:
1) а4 • а5 = а20; 2) а14 : а2 = а7;
3) а5b5 = (аb)10; 4) (a3)3 • а3 = a12?
№ 63. Представьте выражение в виде степени и вычислите его значение:  № 64. Найдите значение выражения:
№ 64. Найдите значение выражения: 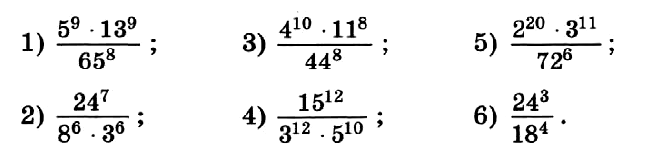
Алгебра 7 Мерзляк С-08 В3
ОТВЕТЫ на самостоятельную работу:
Смотреть РЕШЕНИЯ заданий в тетради
Вы смотрели: Самостоятельная работа по алгебре в 7 классе «Свойства степени с натуральным показателем» с ответами. Дидактические материалы для учителей, учащихся и родителей.
Другие варианты: С-08. Вариант 1 С-08. Вариант 2
Вернуться к Списку самостоятельных работ по алгебре в 7 классе УМК Мерзляк.
Перейти к Списку контрольных работ по алгебре в 7 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 7 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.
Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.
am · an = am + n, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
- Упростить выражение.
b · b2 · b3 · b4 · b5 =
b 1 + 2 + 3 + 4 + 5 = b15 - Представить в виде степени.
615 · 36 = 615 · 62 = 615 · 62 =
617 - Представить в виде степени.
(0,8)3 · (0,8)12 = (0,8)3 + 12 = (0,8)15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями. Оно не относится к их сложению.
Нельзя заменять сумму
(33 + 32) на 35. Это понятно, если
посчитать
(33 + 32) = (27 + 9) = 36 , а
35 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений,
а из показателя степени делимого вычитают показатель степени делителя.
=
am − n, где
«a» — любое
число, не равное нулю, а «m», «n» — любые
натуральные числа такие, что «m > n».
Примеры.
- Записать частное в виде степени
(2b)5 : (2b)3 = (2b)5 − 3 = (2b)2 - Вычислить.
=
113 − 2 · 4 2 − 1 = 11 · 4 = 44 - Пример. Решить уравнение. Используем свойство частного степеней.
38 : t = 34t = 38 : 34
t = 38 − 4
t = 34
Ответ: t = 34 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
45m + 6 · 4m + 2 : 44m + 3 =
45m + 6 + m + 2 : 44m + 3 =
46m + 8 − 4m − 3 = 42m + 5 - Пример. Найти значение выражения, используя свойства степени.
=
==
=
=
211 − 5 = 2 6 = 64
Важно!
Обратите внимание, что в свойстве 2 речь шла только
о делении степеней с одинаковыми основаниями.
Нельзя заменять разность
(43 −42) на 41. Это понятно, если посчитать
(43 −42) = (64 − 16) = 48, а
41 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степень
Запомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней
перемножаются.
(an)m = an · m, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
- Пример.
(a4)6 = a4 · 6 = a24 - Пример. Представить 320 в виде степени с основанием
32.По свойству возведения степени в степень известно, что при возведении
в степень показатели перемножаются, значит:
Свойства 4
Степень произведения
Запомните!
При возведении в степень произведения каждый из множителей
возводится в степень. Затем полученные результаты перемножаются.
(a · b)n = an · bn, где
«a», «b» — любые рациональные
числа; «n» — любое натуральное число.
- Пример 1.
(6 · a2 · b3 · c )2 =
62 · a2 · 2 · b3 · 2
· с 1 · 2 = 36 a4 · b6
· с 2
- Пример 2.
(−x2 · y)6 =( (−1)6 · x2 · 6 · y1 · 6) =
x12 · y6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней,
применяют и в обратном порядке.
(an · bn)=
(a · b) n
То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
24 · 54 = (2 · 5)4 =
104 = 10 000 - Пример. Вычислить.
0,516 · 216 = (0,5 · 2)16 =
1
В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.
Например,
45 · 32 = 43 ·
42 · 32 = 43 · (4 · 3)2 =
64 · 122 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
421 · (−0,25)20 = 4 · 4 20 ·
(−0,25) 20 = 4 · (4 · (−0,25))20 = 4 · (−1)20 =
4 · 1 = 4
Свойства 5
Степень частного (дроби)
Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель,
и первый результат разделить на второй.
(a : b)n = an : bn, где
«a», «b» — любые рациональные
числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3)12 = 512 : 312
Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.
Всего: 37 1–20 | 21–37
Добавить в вариант
Какое из следующих чисел является наименьшим?
В ответе укажите номер правильного варианта.
1) 1,7·10−3
2) 2,3·10−4
3) 4,5·10−3
4) 8,9·10−4
Какое из следующих чисел является наибольшим?
В ответе укажите номер правильного варианта.
1) 1,8·10−3
2) 4,7·10−4
3) 2,9·10−5
4) 9,5·10 −3
Какое из следующих выражений равно ?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Представьте выражение в виде степени с основанием x.
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Представьте выражение в виде степени с основанием
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Представьте выражение в виде степени с основанием
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Представьте выражение в виде степени с основанием x.
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Источник: Банк заданий ФИПИ
Тип 20 № 47
i
Сократите дробь .
Источник: Демонстрационная версия ГИА—2013 по математике., Демонстрационная версия ГИА—2014 по математике.
Какое из следующих выражений равно ?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Найдите значение выражения .
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Представьте выражение в виде степени с основанием c.
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Какому из следующих выражений равна дробь
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Найдите значение выражения
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Найдите значение выражения
Источник: ОГЭ по математике 06.06.2017. Санкт-Петербург. Вариант 1707
Расстояние от Юпитера — одной из планет Солнечной системы — до Солнца равно 778,1 млн км. Как эта величина записывается в стандартном виде?
В ответе укажите номер правильного варианта.
1) 7,781·1011
2) 7,781·108
3) 7,781·1010
4) 7,781·109
Источник: Банк заданий ФИПИ
Масса Луны равна 7,35·1022 кг. Выразите массу Луны в млн тонн.
В ответе укажите номер правильного варианта.
1) 7,35⋅1010 млн т
2) 7,35⋅1013 млн т
3) 7,35⋅1016 млн т
4) 7,35⋅1019 млн т
Вычислите:
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Запишите в ответе номера тех выражений, значение которых равно 0.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
Сравните числа и 12.
В ответе укажите номер правильного варианта.
1)
2)
3)
Источник: Банк заданий ФИПИ
Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?
В ответе укажите номер правильного варианта.
1) 1,471⋅1010 км
2) 1,471⋅108 км
3) 1,471⋅107 км
4) 1,471⋅106 км
Всего: 37 1–20 | 21–37