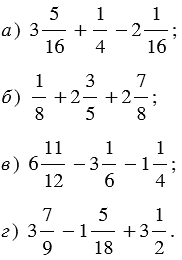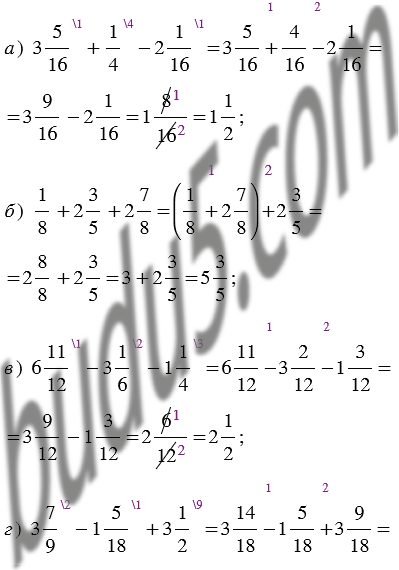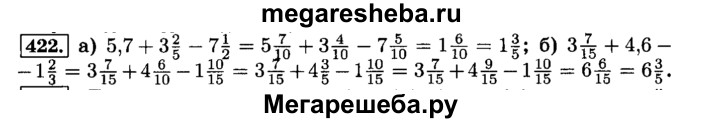Математика 6 класс учебник номер 422

Новая редакция 2018-2023 г.

Вернуться к содержанию учебника

Страница 76

---

Вернуться к содержанию учебника

---

Ответы к учебнику 2019-2021 года

Упражнения

Задание 422

Найдите значение выражения:
а) 1,8 + x при x = 3; 6,8; 0,02; 0;
б) 10 − c при c = 6; 5,5; 10; 0;
в) 4a при a = 1; 0,5; 0;
г) $frac{2}{3}y$ при y = 1; 1,5; 9; 10.

Решение

а) 1,8 + x
при x = 3:
1,8 + 3 = 4,8
при x = 6,8:
1,8 + 6,8 = 8,6
при x = 0,02:
1,8 + 0,02 = 1,82
при x = 0:
1,8 + 0 = 1,8

б) 10 − c
при c = 6:
10 − 6 = 4
при c = 5,5:
10 − 5,5 = 4,5
при c = 10:
10 − 10 = 0
при c = 0:
10 − 0 = 10

в) 4a
при a = 1:
4 * 1 = 4
при a = 0,5:
4 * 0,5 = 2
при a = 0:
4 * 0 = 0

г) $frac{2}{3}y$
при y = 1:
$frac{2}{3} * 1 = frac{2}{3}$
при y = 1,5:
$frac{2}{3} * 1,5 = frac{2}{3} * frac{3}{2} = 1$
при y = 9:
$frac{2}{3} * 9 = 2 * 3 = 6$
при y = 10:
$frac{2}{3} * 10 = frac{20}{3} = 6frac{2}{3}$

Задание 423

Найдите значение выражения:
а) m + 2n при m = 6,4, n = 3,2;
б) 3c − d при c = 1,3, d = 0,9;
в) x + 2y − 3z при x = 10, y = 25, z = 20;
г) a + b − c при $a = frac{2}{3}, b = frac{1}{6}, c = frac{1}{4}.$

Решение

а) m + 2n
при m = 6,4, n = 3,2:
6,4 + 2 * 3,2 = 6,4 + 6,4 = 12,8

б) 3c − d
при c = 1,3, d = 0,9:
3 * 1,3 − 0,9 = 3,9 − 0,9 = 3

в) x + 2y − 3z
при x = 10, y = 25, z = 20:
10 + 2 * 25 − 3 * 20 = 10 + 50 − 60 = 60 − 60 = 0

г) a + b − c
при $a = frac{2}{3}, b = frac{1}{6}, c = frac{1}{4}$:
$frac{2}{3} + frac{1}{6} — frac{1}{4} = frac{2 * 4 + 1 * 2 — 1 * 3}{12} = frac{8 + 2 — 3}{12} = frac{7}{12}$

Задание 424

Найдите значение выражения $frac{a}{c} + 2$:
а) при a = 12, c = 3;
б) при a = 15, c = 10;
в) при a = 1,5, c = 0,5;
г) при $a = frac{1}{2}, c = frac{1}{6}$.

Решение

а) $frac{a}{c} + 2$
при a = 12, c = 3:
$frac{12}{3} + 2 = 4 + 2 = 6$

б) $frac{a}{c} + 2$
при a = 15, c = 10:
$frac{15}{10} + 2 = 1,5 + 2 = 3,5$

в) $frac{a}{c} + 2$
при a = 1,5, c = 0,5:
$frac{1,5}{0,5} + 2 = frac{15}{5} + 2 = 3 + 2 = 5$

г) $frac{a}{c} + 2$
при $a = frac{1}{2}, c = frac{1}{6}$:
$frac{frac{1}{2}}{frac{1}{6}} + 2 = frac{1}{2} * 6 + 2 = 3 + 2 = 5$

Задание 425

Найдите значение выражения $x^2y$;
а) при x = 5, y = 6;
б) при $x = frac{1}{2}, y = 16$;
в) при x = 0,2, y = 10;
г) при x = 100, y = 0,01.

Решение

а) $x^2y$
при x = 5, y = 6:
$x^2y = 5^2 * 6 = 25 * 6 = 150$

б) $x^2y$
при $x = frac{1}{2}, y = 16$:
$x^2y = (frac{1}{2})^2 * 16 = frac{1}{4} * 16 = 4$

в) $x^2y$
при x = 0,2, y = 10:
$x^2y = 0,2^2 * 10 = 0,04 * 10 = 0,4$

г) $x^2y$
при x = 100, y = 0,01:
$x^2y = 100^2 * 0,01 = 10000 * 0,01 = 100$

Задание 426

а) Найдите значение выражения (a + b) + c при a = 0,53, b = 1,27, c = 3,2.
Укажите значение выражения (b + a) + c при этих же значениях букв.
б) Найдите значение выражения (a + b)с при a = 1,6, b = 2,4, c = 2,8.
Укажите значение выражения ac + bc при этих же значениях a, b и c.

Решение

а) (a + b) + c
при a = 0,53, b = 1,27, c = 3,2:
(0,53 + 1,27) + 3,2 = 1,8 + 3,2 = 5
В соответствии с переместительным свойством сложения:
(a + b) + c = (b + a) + c = 5

б) (a + b)с
при a = 1,6, b = 2,4, c = 2,8:
(1,6 + 2,4) * 2,8 = 4 * 2,8 = 11,2
В соответствии с распределительным свойством умножения:
(a + b)с = ac + bc = 11,2

Задание 427

В выражение, содержащее букву a, последовательно подставили три числа. Запишите это буквенное выражение, если в результате подстановок получились следующие числовые выражения:
а)
4 * 11 + 15
4 * 0,8 + 15
$4 * frac{1}{6} + 15$
б)
$40 — 1^2$
$40 — 5^2$
$40 — (0,5)^2$
в)
(3 + 17) * 4
(3 + 1,6) * 4
$(3 + frac{4}{9}) * 4$

Решение

а) 4 * a + 15
4 * 11 + 15 = 44 + 15 = 59;
4 * 0,8 + 15 = 3,2 + 15 = 18,2;
$4 * frac{1}{6} + 15 = frac{2}{3} + 15 = 15frac{2}{3}$.

б) $40 — a^2$
$40 — 1^2 = 40 — 1 = 39$;
$40 — 5^2 = 40 — 25 = 15$;
$40 — (0,5)^2 = 40 — 0,25 = 39,75$.

в) (3 * a) * 4
(3 + 17) * 4 = 20 * 4 = 80;
(3 + 1,6) * 4 = 4,6 * 4 = 18,4;
$(3 + frac{4}{9}) * 4 = 3frac{4}{9} * 4 = frac{31}{9} * 4 = frac{124}{9} = 13frac{7}{9}$.

Задание 428

Сравните значения выражений:
а) (1 + a)b и 1 + ab при a = 3 и b = 2,5;
б) $(1 — a)^2$ и $1 — a^2$ при a = 0,1;
в) $a^2 — b^2$ и (a − b)(a + b) при a = 0,7 и b = 0,3;
г) $a^2 + b^2 + 2ab$ и $(a + b)^2$ при a = 1 и b = 0,5.

Решение

а) при a = 3 и b = 2,5:
(1 + a)b = (1 + 3) * 2,5 = 4 * 2,5 = 10;
1 + ab = 1 + 3 * 2,5 = 1 + 7,5 = 8,5;
10 > 8,5 − значит:
(1 + a)b > 1 + ab.

б) при a = 0,1:
$(1 — a)^2 = (1 — 0,1)^2 = 0,9^2 = 0,81$;
$1 — a^2 = 1 — 0,1^2 = 1 — 0,01 = 0,99$;
0,81 < 0,99 − значит:
$(1 — a)^2 < 1 — a^2$.

в) при a = 0,7 и b = 0,3:
$a^2 — b^2 = 0,7^2 — 0,3^2 = 0,49 — 0,09 = 0,4$;
(a − b)(a + b) = (0,7 − 0,3)(0,7 + 0,3) = 0,4 * 1 = 0,4;
0,4 = 0,4 − значит:
$a^2 — b^2 = (a — b)(a + b)$.

г) при a = 1 и b = 0,5:
$a^2 + b^2 + 2ab = 1^2 + 0,5^2 + 2 * 1 * 0,5 = 1 + 0,25 + 1 = 2,25$;
$(a + b)^2 = (1 + 0,5)^2 = 1,5^2 = 2,25$;
2,25 = 2,25 − значит:
$a^2 + b^2 + 2ab = (a + b)^2$.

Задание 429

Какие из чисел 0, 10, 20, 25, 30 являются допустимыми значениями буквы x в выражении $frac{25 — x}{x}$?

Решение

$frac{25 — x}{x}$
при x = 0:
$frac{25 — 0}{0}$ − недопустимо, так как на 0 делить нельзя.
при x = 10:
$frac{25 — 10}{10} = frac{15}{10} = 1,5$ − допустимо.
при x = 20:
$frac{25 — 20}{20} = frac{5}{20} = 0,25$ − допустимо.
при x = 25:
$frac{25 — 25}{25} = frac{0}{25} = 0$ − допустимо.
при x = 30:
$frac{25 — 30}{30}$ − недопустимо, так как в числителе вычитается большее число из меньшего.
Ответ: 10, 20, 25.

Имеется 3 комнаты с разными замками и 3 ключа от этих комнат. Какое наименьшее число проб нужно сделать, чтобы определить, какой ключ от какой комнаты?