Номер № 350
350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
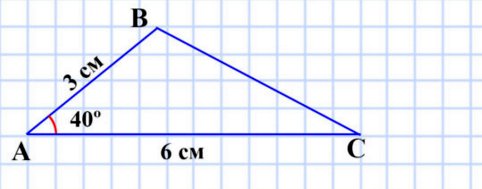
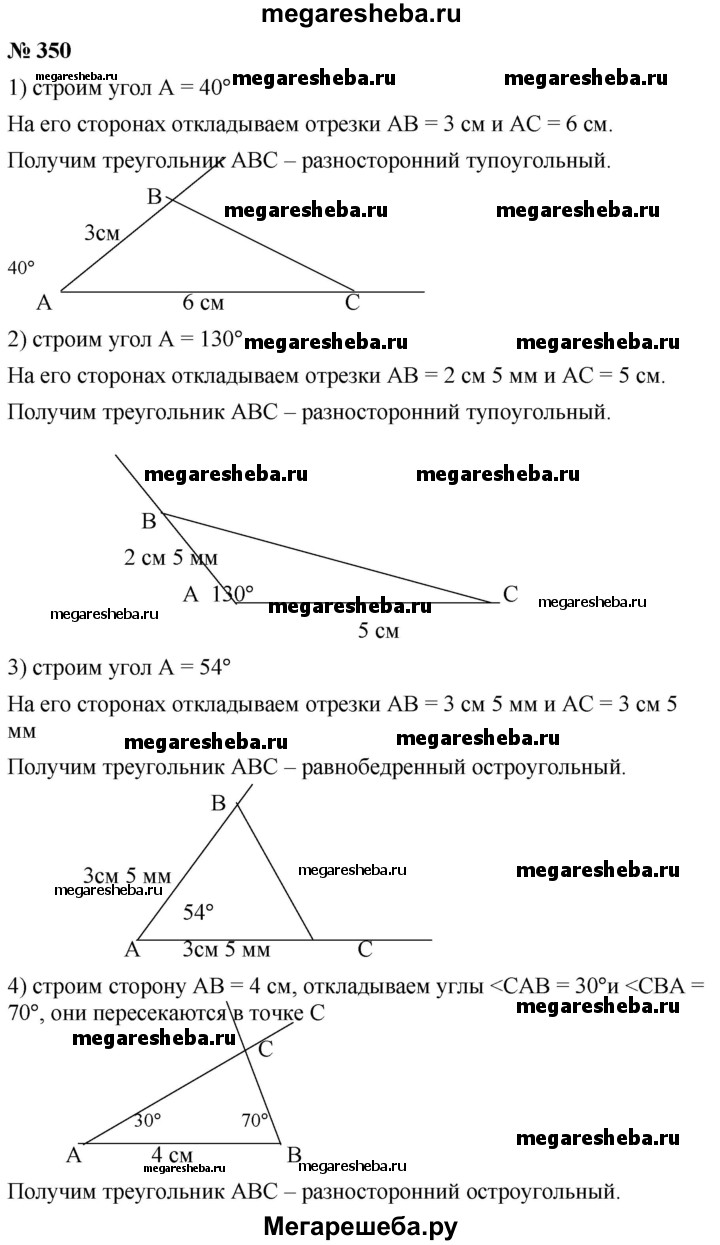
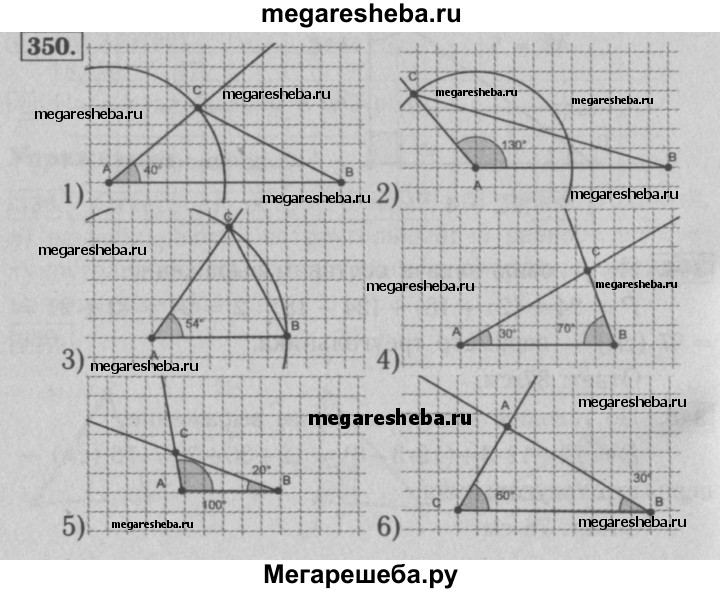
1) две стороны равны 3 см и 6 см, а угол между ними — 40°
Разносторонний тупоугольный треугольник.
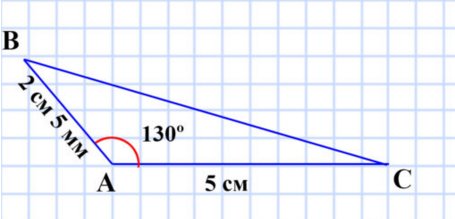
2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130°
Разносторонний тупоугольный треугольник.
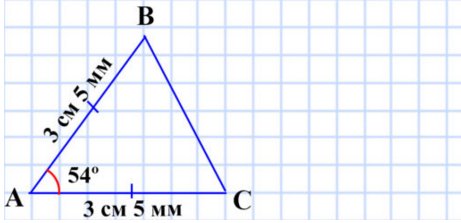
3) две стороны равны по 3 см 5 мм, а угол между ними — 54°
Равнобедренный остроугольный треугольник.
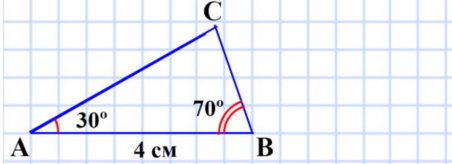
4) сторона АВ равна 4 см, а углы САВ и CBA соответственно равны 30° и 70°
Разносторонний остроугольный треугольник.
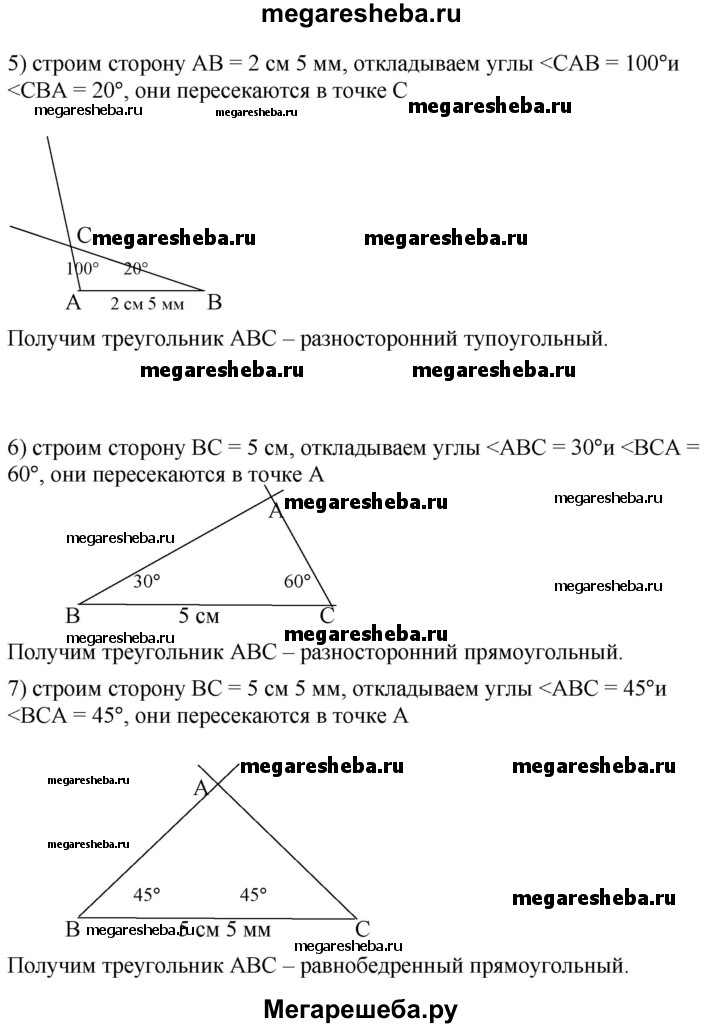
5) сторона АВ равна 2 см 5 мм, а углы САВ и CBA соответственно равны 100° и 20°
Разносторонний тупоугольный треугольник.
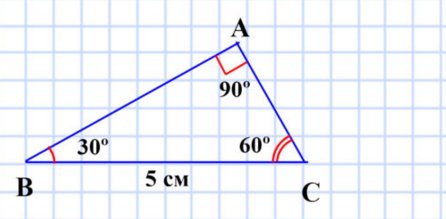
6) сторона ВС равна 5 см, а углы ABC и BCA соответственно равны 30° и 60°
Разносторонний прямоугольный треугольник.
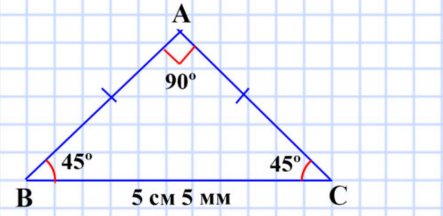
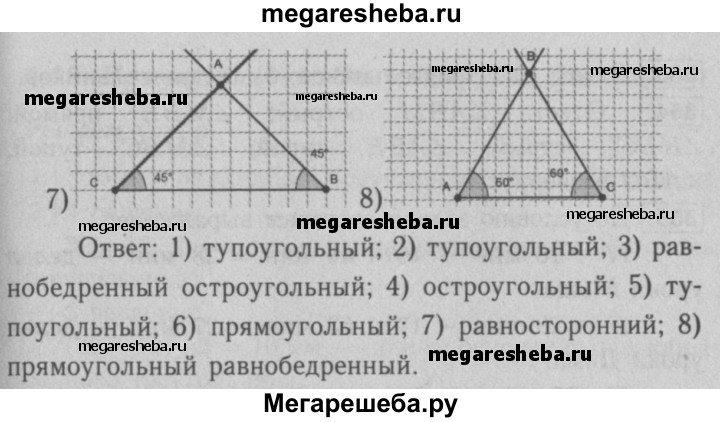
7) сторона ВС равна 5 см 5 мм, а углы ABC и BCA равны по 45°
Равнобедренный прямоугольный треугольник.
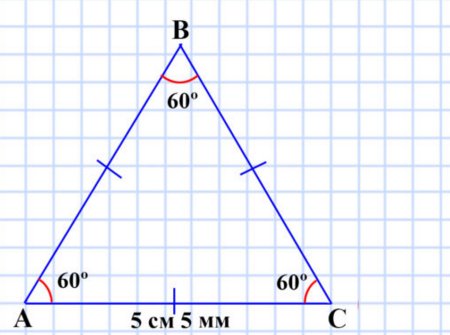
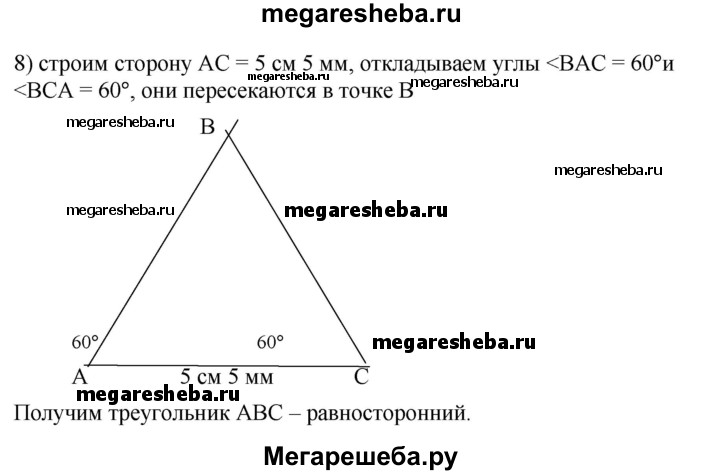
сторона АС равна 5 см 5 мм, а углы ВАС и BCA равны по 60°
Равносторонний остроугольный.
Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его:
Показать содержание
← Предыдущее
Следующее →
Решебник
§6 / 350
Показать содержание
← Предыдущее
Следующее →
Условие /
номер / 350
350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
1) две стороны равны 3 см и 6 см, а угол между ними — 40°;
2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130°;
3) две стороны равны по 3 см 5 мм, а угол между ними — 54°;
4) сторона АВ равна 4 см, а углы CAB и СВА соответственно равны 30° и 70°;
5) сторона АВ равна 2 см 5 мм, а углы CAB и СВА соответственно равны 100° и 20°;
6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60°;
7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45°;
сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60°.
Решебник №1 к учебнику 2015 / номер / 350
Решебник к учебнику 2021 / номер / 350
Видеорешение / номер / 350
Решебник №2 к учебнику 2015 / номер / 350
Ответы к упражнениям
Задание 350. Делится ли произведение 6 * 14 на 2? на 3? на 7? Почему?
Решение
6 * 14 = (3 * 2) * (7 * 2) − делится на 2, так как каждый множитель делится на 2;
6 * 14 = (2 * 3) * 14 = 3 * (2 * 14) − делится на 3, так как один из множителей делится на 3;
6 * 14 = 6 * (7 * 2) = 7 * (6 * 2) − делится на 7, так как один из множителей делится на 7.
Задание 351. Не выполняя действий, докажите, что произведение:
а) 322 * 15 делится на 5;
б) 401 * 16 делится на 4;
в) 25 * 6 * 14 делится на 2, на 3, на 5, на 4, на 10;
г) 12 * 22 * 35 делится на 2, на 3, на 5, на 4, на 15, на 77.
Решение
а) 322 * 15 = 322 * (5 * 3) = 5 * (322 * 3)
б) 401 * 16 = 401 * (4 * 4) = 4 * (401 * 4)
в) 25 * 6 * 14 = 25 * (2 * 3) * 14 = 2 * (25 * 3 * 14);
25 * 6 * 14 = 25 * (3 * 2) * 14 = 3 * (25 * 2 * 14);
25 * 6 * 14 = 25 * 6 * 14 = (5 * 5) * 6 * 14 = 5 * (5 * 6 * 14);
25 * 6 * 14 = 25 * (2 * 3) * (2 * 7) = (2 * 2) * (25 * 3 * 7) = 4 * (25 * 3 * 7);
25 * 6 * 14 = (5 * 5) * (2 * 3) * 14 = (2 * 5) * (5 * 3 * 14) = 10 * (5 * 3 * 14).г) 12 * 22 * 35 = (2 * 6) * 22 * 35 = 2 * (6 * 22 * 35);
12 * 22 * 35 = (3 * 4) * 22 * 35 = 3 * (4 * 22 * 35);
12 * 22 * 35 = 12 * 22 * (5 * 7) = 5 * (12 * 22 * 7);
12 * 22 * 35 = (4 * 3) * 22 * 35 = 4 * (3 * 22 * 35);
12 * 22 * 35 = (3 * 4) * 22 * (5 * 7) = (3 * 5) * (4 * 22 * 7) = 15 * (4 * 22 * 7);
12 * 22 * 35 = 12 * (11 * 2) * (7 * 5) = (11 * 7) * (12 * 2 * 5) = 77 * (12 * 2 * 5).
Задание 352. а) Укажите какие−нибудь пять делителей произведения 16 * 12.
б) Укажите какие−нибудь десять делителей произведения 32 * 24 * 21.
Решение
а) 16 * 12 = (2 * 2 * 2 * 2) * (2 * 2 * 3);
2 * 2 = 4;
2 * 2 * 2 = 8;
2 * 3 = 6.
Пять делителей: 2, 3, 4, 6, 8.б) 32 * 24 * 21 = (2 * 2 * 2 * 2 * 2) * (2 * 2 * 2 * 3) * (3 * 7);
2 * 2 = 4;
2 * 2 * 2 = 8;
2 * 2 * 2 * 2 = 16;
2 * 3 = 6;
2 * 2 * 3 = 12;
2 * 7 = 14;
3 * 3 = 9.
Десять делителей: 2, 3, 4, 6, 7, 8, 9, 12, 14, 16.
Задание 353. 1) Известно, что некоторое число делится на 10. Делится ли оно на 2? на 5? Ответ объясните.
2) Число a делится на 36. Укажите еще несколько делителей этого числа.
Решение
1) 10 = 2 * 5 − значит, данное число делится и на 2 и на 5.
2) 36 = 2 * 2 * 3 * 3
2 * 2 = 4;
2 * 3 = 6;
2 * 2 * 3 = 12;
2 * 3 * 3 = 18, значит данное число будет делиться на:
2, 3, 4, 6, 12, 18.
Задание 354. а) Известно, что некоторое число делится на 4. Можно ли утверждать, что оно делится на 2?
б) Известно, что некоторое число делится на 2. Можно ли утверждать, что оно делится на 4?
Решение
а) 4 = 2 * 2 − значит, если число делится на 4, можно утверждать, что оно делится на 2.
б) если число делится на 2, нельзя утверждать, что оно делится на 4, например:
число 6 делится на 2, но не делится на 4.
Задание 355. Укажите три числа, которое можно подставить вместо буквы a, чтобы произведение:
а) 36 * a делилось на 14;
б) 15 * a было кратно 20.
Решение
а) $36 * a = 2^2 * 3^2 * a$;
14 = 2 * 7;
при a = 7, 14, 28:
36 * a − будет делиться на 14.б) 15 * a = 3 * 5 * a;
20 = 4 * 5;
при a = 4, 8, 12:
15 * a − будет кратно 20.
Задание 356. Докажите, не выполняя действий, что сумма делится на 2, на 3 и на 4:
а) 60 + 48 + 24;
б) 12 + 36 + 24 + 48.
Решение
а) 60 + 48 + 24 = (2 * 30) + (2 * 24) + (2 * 12) = 2 * (30 + 24 + 12);
60 + 48 + 24 = (3 * 20) + (3 * 16) + (3 *
60 + 48 + 24 = (4 * 15) + (4 * 12) + (4 * 6) = 4 * (15 + 12 + 6).б) 12 + 36 + 24 + 48 = (2 * 6) + (2 * 18) + (2 * 12) + (2 * 24) = 2 * (6 + 18 + 12 + 24);
12 + 36 + 24 + 48 = (3 * 4) + (3 * 12) + (3 *
12 + 36 + 24 + 48 = (4 * 3) + (4 * 9) + (4 * 6) + (4 * 12) = 4 * (3 + 9 + 6 + 12).
Задание 357. Делится ли сумма:
а) 25 + 35 + 15 + 45 на 5;
б) 14 + 21 + 63 + 24 на 7;
в) 18 + 36 + 55 + 90 на 9;
г) 50000 + 8000 + 700 + 20 на 10?
Решение
а) 25 + 35 + 15 + 45 = (5 * 5) + (5 * 7) + (5 * 3) + (5 * 9) = 5 * (5 + 7 + 3 + 9)
Ответ: делится на 5.б) 14 + 21 + 63 + 24 = (7 * 2) + (7 * 3) + (7 * 9) + 24
Ответ: не делится на 7, так как 24 не делится на 7.в) 18 + 36 + 55 + 90 = (9 * 2) + (9 * 4) + 55 + (9 * 10)
Ответ: не делится на 9, так как 55 не делится на 9.г) 50000 + 8000 + 700 + 20 = (10 * 5000) + (10 * 800) + (10 * 70) + (10 * 2) = 10 * (5000 + 800 + 70 + 2)
Ответ: делится на 10.
Задание 358. Подберите такие три числа, чтобы при подстановке каждого из них вместо буквы a сумма:
а) 40 + a делилась на 8;
б) 45 + a не делилась на 15;
в) a + 72 была кратна 9;
г) a + 36 не была кратна 3.
Решение
а) 40 + 8 = (8 * 5) + (8 * 1) = 8 * (5 + 1);
40 + 16 = (8 * 5) + (8 * 2) = 8 * (5 + 2);
40 + 24 = (8 * 5) + (8 * 3) = 8 * (5 + 3).
Ответ: a = 8, 16, 24.б) 45 + 1 = (15 * 3) + 1;
45 + 2 = (15 * 3) + 2;
45 + 3 = (15 * 3) + 3.
Ответ: a = 1, 2, 3.в) 9 + 72 = (9 * 1) + (9 *
18 + 72 = (9 * 2) + (9 *
27 + 72 = (9 * 3) + (9 *
Ответ: a = 9, 18, 27.г) 1 + 36 = 1 + (3 * 12);
2 + 36 = 2 + (3 * 12);
4 + 36 = 4 + (3 * 12).
Ответ: a = 1, 2, 4.
Задание 359. Докажите, что разность 15 * 316 − 15 * 114 делится на 15. Сформулируйте соответствующее свойство разности.
Подсказка.
Вынесите число 15 за скобки.
Решение
15 * 316 − 15 * 114 = 15 * (316 − 114) − делится на 15.
Если уменьшаемое и вычитаемое делится на какое−либо число, то и вся разность делится на это число.