-
Главная
-
ГДЗ
- 5 класс
- Математика
-
Мерзляк учебник
- 329
Вернуться к содержанию учебника
Сложение и вычитание натуральных чисел. Упражнения § 13. Страница 88
Вопрос
1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) n — угольника, где n > 3?
2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в n — угольнике, где n > 3?
Подсказка
Вспомните, что такое:
- Многоугольник.
- Диагональ многоугольника.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
Показать содержание
← Предыдущее
Следующее →
Решебник №1
глава 1 / 329
Решебник №2
глава 1 / 329
Решебник №3
глава 1 / 329
Решебник №4
глава 1 / 329
Решебник №6
глава 1 / 329
Решебник №7
глава 1 / 329
Показать содержание
← Предыдущее
Следующее →
Авторы: , В.Б. Полонский, М.С. Якир.
Издательства:
Просвещение, Вентана-граф 2016-2021
Тип: Учебник, Алгоритм успеха
Подробный решебник (ГДЗ) по Математике за 5 (пятый) класс — готовый ответ номер — 329. Авторы учебника: Мерзляк, Полонский, Якир. Издательство: Вентана-граф 2016-2021.
Условие /
номер / 329
329. 1) Сколько диагоналей можно провести из одной вершины:
а) пятиугольника;
б) девятиугольника;
в) в n-угольнике, где n > 3?
2) Сколько всего диагоналей можно провести:
а) в пятиугольнике;
б) в девятиугольнике;
в) в n-угольнике, где n > 3?
Решебник №1 к учебнику 2015 / номер / 329
Решебник к учебнику 2021 / номер / 329
Видеорешение / номер / 329
Решебник №2 к учебнику 2015 / номер / 329
Оцените решебник:
4.4/5
20150
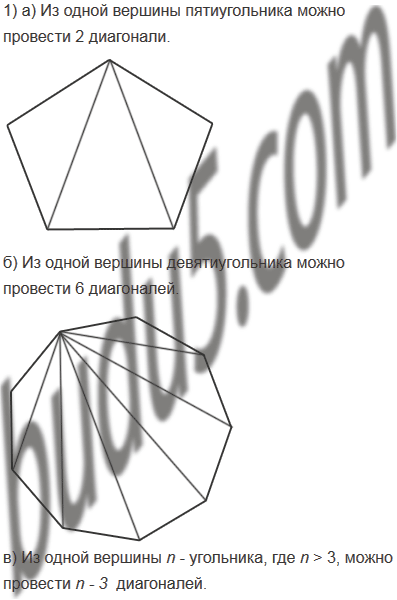
1) Сколько диагоналей можно провести из одной вершины:
а) пятиугольника;
б) девятиугольника;
в) n − угольника, где n > 3?
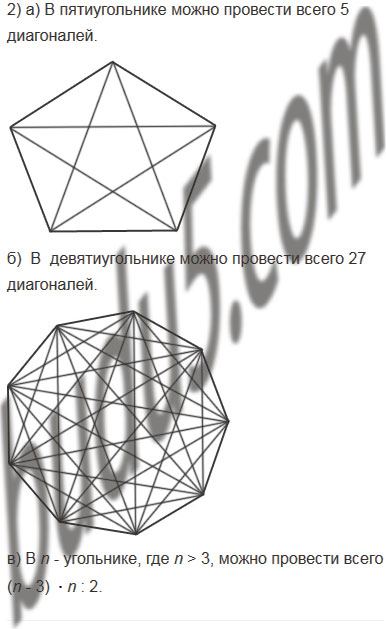
2) Сколько всего диагоналей можно провести:
а) в пятиугольнике;
б) в девятиугольнике:
в) n − угольнике, где n > 3?
reshalka.com
Математика 5 класс Мерзляк. Номер №329
Решение 1
а) Всего вершин 5 − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = 2, то есть в пятиугольнике из одной вершины можно провести только две диагонали;
б) Всего вершин 9 − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = 6, то есть в девятиугольнике из одной вершины можно провести только 6 диагоналей;
в) Всего вершин n − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = n − 3, то есть в n − угольнике из одной вершины можно провести только n − 3 диагоналей.
Решение 2
а) Из каждой вершины пятиугольника можно провести по 2 диагонали, одна (половина) из которых будет совпадать с диагональю от другой вершины, следовательно: (5 * 2) : 2 = 5 диагоналей можно провести в пятиугольнике;
б) Из каждой вершины девятиугольника можно провести по 6 диагоналей, половина из которых будет совпадать с диагоналями от другой вершины, следовательно: (9 * 6) : 2 = 27 диагоналей можно провести в девятиугольнике;
в) Из каждой вершины n − угольника можно провести по n − 3 диагоналей, половина из которых будет совпадать с диагоналями от другой вершины, следовательно:
(
n
∗
(
n
−
3
)
)
:
2
=
(
n
2
−
3
n
)
:
2
диагоналей можно провести в n − угольнике.