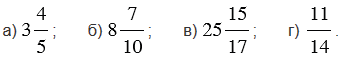-
Главная
-
ГДЗ
- 5 класс
- Математика
-
Виленкин учебник
- 235
Новая редакция 2018-2023 г.
Смотрите также:
- Учебник старой редакции (2011 — 2017 г.)
Вернуться к содержанию учебника
Страница 47
Вопрос
Представьте число в виде суммы его целой и дробной частей:
Подсказка
Вспомните:
- Смешанные числа.
- Правильные дроби.
- Натуральные числа.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
Смотрите также:
- Учебник старой редакции (2011 — 2017 г.)
Выполните деление:
а) 261 : 7;
б) 1872 : 8;
в) 2144 : 6;
г) 1742 : 13;
д) 3685 : 15;
е) 15216 : 16.
reshalka.com
Математика 5 класс Никольский. Номер №235
Решение а
261 : 7 = 37 (ост.2)
0
¯
261
0
21
¯
0
0
¯
51
00
49
¯
000
2
7
37
¯
Решение б
1872 : 8 = 234
0
¯
1872
0
16
¯
0
0
¯
27
00
24
¯
00
0
¯
32
000
32
¯
0000
0
8
234
¯
Решение в
2144 : 6 = 357 (ост.2)
0
¯
2144
0
18
¯
0
0
¯
34
00
30
¯
00
0
¯
44
000
42
¯
0000
2
6
357
¯
Решение г
1742 : 13 = 134
0
¯
1742
0
13
¯
0
0
¯
44
00
39
¯
00
0
¯
52
000
52
¯
0000
0
13
134
¯
Решение д
3685 : 15 = 245 (ост.10)
0
¯
3685
0
30
¯
0
0
¯
68
00
60
¯
00
0
¯
85
000
75
¯
000
10
15
245
¯
Решение е
15216 : 16 = 951
0
¯
15216
0
144
¯
00
0
¯
81
000
80
¯
000
0
¯
16
0000
16
¯
00000
0
16
951
¯
Показать содержание
← Предыдущее
Следующее →
Решебник
§2 / 235
Показать содержание
← Предыдущее
Следующее →
Авторы: , В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Издательство:
Мнемозина
Тип: Учебник
Подробный решебник (ГДЗ) по Математике за 5 (пятый) класс — готовый ответ глава 1 § 2 тема 6 — 235. Авторы учебника: Виленкин, Жохов, Чесноков, Шварцбурд. Издательство: Мнемозина .
Условие /
глава 1 / § 2 / тема 6 / 235
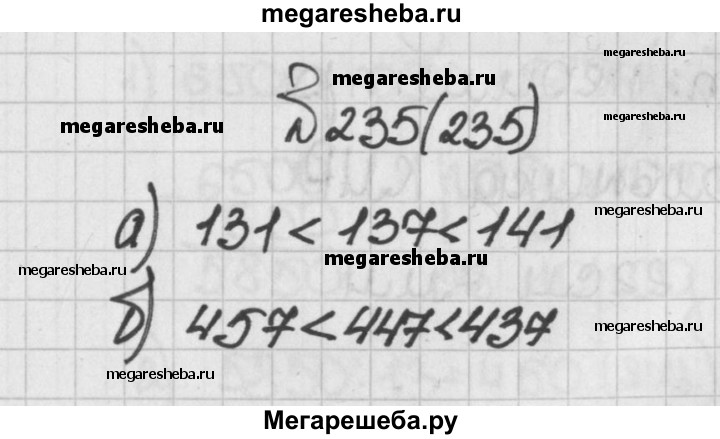
235. Найдите число, оканчивающееся цифрой 7, если оно: а) больше 131 и меньше 141; б) меньше 457 и больше 437.
Решебник №1 / глава 1 / § 2 / тема 6 / 235
Видеорешение / глава 1 / § 2 / тема 6 / 235
Решебник №2 / глава 1 / § 2 / тема 6 / 235
Решебник №3 / глава 1 / § 2 / тема 6 / 235
Оцените решебник:
4.4/5
19409
Номер № 235
235. В двузначном числе 6 десятков. Между цифрами этого числа вписали цифру 0. На сколько полученное трёхзначное число больше, чем данное двузначное?
Предположим, что в указанном двузначном числе 6 десятков и 0 единиц, то есть это число 60. Если вписать между цифрами 0, то получим число 600.
Найдём, насколько полученное трёхзначное число больше исходного двузначного: 600 – 60 = 540.
Предположим, что в указанном двузначном числе 6 десятков и 1 единица, то есть это число 61. Если вписать между цифрами 0, то получим число 601.
Найдём, насколько полученное трёхзначное число больше исходного двузначного: 601 – 61 = 540.
Предположим, что в указанном двузначном числе 6 десятков и 2 единицы, то есть это число 62. Если вписать между цифрами 0, то получим число 602.
Найдём, насколько полученное трёхзначное число больше исходного двузначного: 602 – 62 = 540.
Мы видим, что не зависимо от того, какая цифра стоит на месте единиц, разность между исходным двузначным числом и полученным трёхзначным одинакова.
Ответ: на 540.
Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его: