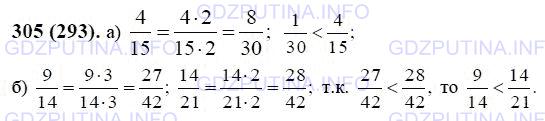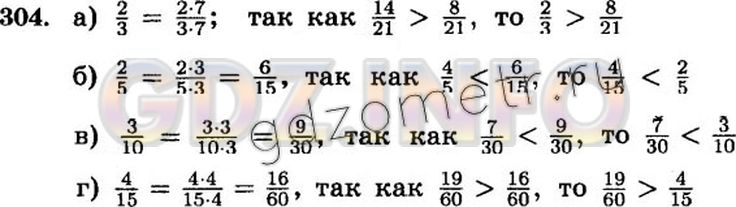2013г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №305 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №305 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие
20132019г.
Что меньше: а) 4/15 или 1/30; б) 9/14 или 14/21?
Приведите дроби к наименьшему общему знаменателю:
а) 5/7 и 1/2; в) 3/26 и 5/36; д) 7/13 и 2/11; ж) 7/60, 13/540 и 9/20;
б) 7/20 и 1/15; г) 8/11 и 5/8; е) 3/22 и 2/33; з) 52/105, 7/95 и 61/63.
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Вычислите столбиком:
а) 123 * 9;
б) 357 * 8;
в) 256 * 32;
г) 457 * 48;
д) 521 * 32;
е) 439 * 528.
reshalka.com
Математика 6 класс Никольский. Номер №305
Решение
Решение:
а)
×
123
9
¯
1107
;
б)
×
357
8
¯
2856
;
в)
×
256
32
¯
512
768
0
8192
¯
;
г)
×
457
48
¯
3656
1828
0
21936
¯
;
д)
×
521
32
¯
1042
1563
0
16672
¯
;
е)
×
439
528
¯
3512
878
0
2195
00
231792
¯
.
Ответ:
а) 1107;
б) 2856;
в) 8192;
г) 21936;
д) 16672;
е) 231792.
-
Главная
-
ГДЗ
- 6 класс
- Математика
-
Мерзляк учебник
- 305
Вернуться к содержанию учебника
Обыкновенные дроби. Упражнения § 10. Страница 61
Вопрос
Пётр Ленивцев может покрасить стену за 24 ч, а Иван Трудолюб — за 8 ч. Какая часть стены останется неокрашенной после 1 ч совместной работы Ленивцева и Трудолюба?
Подсказка
Вспомните:
- Обыкновенные дроби.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему множителю.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
Показать содержание
← Предыдущее
Следующее →
Решебник
часть 1 / 305
Показать содержание
← Предыдущее
Следующее →
Задание 305. Многоугольник, изображенный на рисунке 5.21, а, называют снежинкой Коха. Постройте ее. Для этого:
1) начертите на листе нелинованной бумаги равносторонний треугольник со стороной 9 см (рис. 5.21, б);
2) каждую сторону треугольника разделите на 3 равные части и на средней части постройте равносторонний треугольника (рис. 5.21, в);
3) повторите это построение на каждой из 12 сторон получившегося многоугольника (рис. 5.21, г);
4) чтобы получить снежинку, изображенную на рисунке 5.21, а, надо сделать еще один шаг построения.
Задание 306. ЗАДАЧА−ИССЛЕДОВАНИЕ
Во сколько раз увеличивается число сторон снежинки Коха на каждом шаге построения (см. рис. 5.21)? Во сколько раз при этом уменьшается длина ее стороны? Для каждого шага построения определите число сторон снежинки и ее периметр.
Решение
Число сторон снежинки Коха на каждом шаге построения увеличивается в 4 раза.
Шаг 1:
3 − число сторон;
9 (см) − длина стороны;
3 * 9 = 27 (см) − периметр.
Шаг 2:
3 * 4 = 12 − число сторон;
9 : 3 = 3 (см) − длина стороны;
12 * 3 = 36 (см) − периметр.
Шаг 3:
12 * 4 = 48 − число сторон;
3 : 3 = 1 (см) − длина стороны;
48 * 1 = 48 (см) − периметр.
Шаг 4:
48 * 4 = 192 − число сторон;
$1 : 3 = frac{1}{3}$ (см) − длина стороны;
$192 * frac{1}{3} = 64$ (см) − периметр.
Неравенство треугольника
Задание 307. 1) Убедитесь, что нельзя построить треугольник, стороны которого равны:
а) 7 см, 3 см и 3 см;
б) 6 см, 4 см и 2 см.
измените длину одной из сторон так, чтобы треугольник можно было построить.
2) Можно ли построить треугольник со сторонами:
а) 11 см, 13 см, 25 см;
б) 15 см, 6 см, 12 см;
в) 20 см, 18 см, 38 см?
Решение
1) а)
7 + 3 = 10 > 3;
7 + 3 = 10 > 3;
3 + 3 = 6 < 7 − значит, треугольник построить нельзя.
Увеличим одну из сторон, равную 3 см на 2 см, получим треугольник со сторонами: 7 см, 5 см, 3 см. Тогда:
7 + 5 = 12 > 3;
7 + 3 = 10 > 5;
3 + 5 = 8 > 7 − значит, треугольник построить можно.
б)
6 + 4 = 10 > 2;
6 + 2 = 8 > 4;
4 + 2 = 6 = 6 − значит, треугольник построить нельзя.
Увеличим сторону, равную 2 см на 1 см, получим треугольник со сторонами 6 см, 4 см, 3 см. Тогда:
4 + 3 = 7 > 6;
6 + 4 = 10 > 3;
6 + 3 = 9 > 4 − значит, треугольник построить можно.2) а)
11 + 25 = 36 > 13;
13 + 25 = 38 > 11;
11 + 13 = 24 < 25 − значит, треугольник построить нельзя.
б)
12 + 6 = 18 > 15;
12 + 15 = 27 > 6;
15 + 6 = 21 > 12 − значит, треугольник построить можно.
в)
20 + 38 = 58 > 18;
18 + 38 = 56 > 20;
20 + 18 = 38 = 38 − значит, треугольник построить нельзя.
Ответ:
а) нельзя;
б) можно;
в) нельзя.
Задание 308. В равнобедренным треугольнике одна сторона равна 7 см, а другая − 15 см. Какая сторона является основанием?
Решение
Пусть 15 см − основание, тогда:
7 (см) − вторая боковая сторона;
7 + 7 = 14 < 15, значит, основание не может быть 15 см.
Ответ: 7 см − основание.
Задание 309. Даны четыре отрезка длиной 2 см, 3 см, 5 см и 6 см. Сколько различных разносторонних треугольников можно построить из этих отрезков?
Решение
Вариант 1. Треугольник со сторонами 2 см, 3 см, 5 см.
2 + 5 = 7 > 3;
3 + 5 = 8 > 2;
2 + 3 = 5 = 5 − значит, треугольник построить нельзя.Вариант 2. Треугольник со сторонами 2 см, 5 см, 6 см.
2 + 5 = 7 > 6;
6 + 5 = 11 > 2;
2 + 6 = 8 > 5 − значит, треугольник построить можно.Вариант 3. Треугольник со сторонами 2 см, 3 см, 6 см.
2 + 6 = 8 > 3;
3 + 6 = 9 > 2;
2 + 3 = 5 < 6 − значит, треугольник построить нельзя.Вариант 4. Треугольник со сторонами 3 см, 5 см, 6 см.
3 + 5 = 8 > 6;
3 + 6 = 9 > 5;
5 + 6 = 11 > 3 − значит, треугольник построить можно.
Ответ: можно построить треугольники со сторонами:
2 см, 5 см, 6 см;
3 см, 5 см, 6 см.