Координаты вектора
27.03.2020.
Тест. Геометрия, 11 класс
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Список вопросов теста
Вопрос 1
Пользуясь разложением вектора по координатным векторам, определите его координаты.
Варианты ответов
- {-2; 3; -7}
- {2; 3; 7}
- {3; -2; -7}
- {-7; 3; -2}
Вопрос 2
Установите соответствие между разложениями векторов по координатным векторам и их координатами.
Варианты ответов
- {2; 3; 2}
- {2; 0; 2}
- {0; 3; 2}
- {2; 3; -2}
- {0; 0; 2}
Вопрос 3
Установите порядок записи координат некоторого вектора в пространстве {…; …; …}.
Варианты ответов
- абсцисса
- ордината
- аппликата
Вопрос 4
Пользуясь координатами векторов и тем, что начало каждого из них совпадает с точкой О начала координат, определите координатные плоскости, в которых они лежат.
1.
Вектор с координатами {3; -8,2; 0}
2.
Вектор с координатами {0; 4,1; 7}
3.
Вектор с координатами C {5; 0; 12}
4.
Вектор с координатами {1; 11; -6}
Варианты ответов
- лежит в координатной плоскости Oxy.
- лежит в координатной плоскости Oyz.
- лежит в координатной плоскости Oxz.
- не лежит ни в одной из координатных плоскостей.
Вопрос 5
Укажите, какие условия для координат вектора должны выполняться, чтобы она лежал или был параллелен оси Oy.
Варианты ответов
- Абсцисса равна 0.
- Абсцисса не равна 0.
- Ордината равна 0.
- Ордината не равна 0.
- Аппликата равна 0.
- Аппликата не равна 0.
Вопрос 6
Укажите, вектор с какими координатами будет являться противоположным координатному вектору .
Варианты ответов
- {-1; 0; 0}
- {0; -1; 0}
- {0; 0; -1}
- {-1; -1; -1}
Вопрос 10
Пользуясь данными рисунка, определите координаты вектора . В ответе укажите координаты вектора по образцу {1;-5;3,5} без пробелов.
Тест по геометрии
«Векторы. Метод координат»
Тест
по теме «Векторы. Метод координат»
Вариант
1
1. Направленный
отрезок (вектор) – это…
а) отрезок,
имеющий начало и конец;
б) отрезок,
для которого указано, какая точка является началом, а какая – концом;
в) прямая,
для которой определено направление;
г) нет
правильного ответа.
2. Коллинеарные
векторы – это…
а) векторы,
лежащие на одной прямой или на параллельных прямых;
б) векторы,
не лежащие на одной прямой или на параллельных прямых;
в) ненулевые
векторы, не лежащие на одной прямой или на параллельных прямых;
г) ненулевые
векторы, лежащие на одной прямой или на параллельных прямых.
3. Противоположно
направленные векторы – это…
а) векторы,
направленные в одну сторону;
б) ненулевые
векторы, направленные в разные сторону;
в) ненулевые
коллинеарные векторы, направленные в одну сторону;
г) ненулевые
коллинеарные векторы, направленные в разные стороны.
4. Как
называется отрезок, для которого указано, какая из его граничных точек
считается началом, а какая концом?
а) луч;
б) модуль;
в) прямая;
г) вектор.
5. Какие
векторы на рисунке коллинеарны?
а) MN, OZ, CD, PK;
б) WX, PK, MN;
в) PK, MN;
г) PK, CD, MN, WX
6. Если любая
точка плоскости является вектором, то, как она называется?
а) нулевой вектор;
б) равный вектор
7. Определите
координаты вектора , если и ![]() :
:
8. Найдите координаты
вектора ![]() , зная координаты его начала и конца:
, зная координаты его начала и конца: ![]()
![]() .
.
9. Найдите длину
вектора ![]() :
:
а) – 36;
б) – 6;
в) 6;
г) 36.
10. Найдите координаты
вектора ![]() , если
, если ![]() ,
, ![]() и
и ![]() .
.
Тест
по теме «Векторы. Метод координат»
Вариант
2
1.
Модуль
ненулевого вектора ![]() – это…
– это…
а) длина
отрезка АВ;
б) коэффициент
разложения вектора АВ;
в) направление
вектора ![]() ;
;
г) направление
отрезка АВ.
2.
Сонаправленные
векторы – это…
д) векторы,
направленные в одну сторону;
е) ненулевые
векторы, направленные в одну сторону;
ж) ненулевые
коллинеарные векторы, направленные в одну сторону;
з) ненулевые
коллинеарные векторы, направленные в разные стороны.
3.
Равные
векторы – это…
и) векторы,
длины которых равны;
к) сонаправленные
векторы, длины которых равны;
л) противоположно
направленные векторы, длины которых равны;
м) коллинеарные
векторы, длины которых равны.
4.
Как
называется правило сложения неколлинеарных двух векторов?
а)
правило Пифагора;
б) правило параллельных прямых;
в) правило равенства треугольника;
г) правило треугольника.
5. Сонаправленные
векторы изображены на рисунке?

а) а;
б) б;
в) в;
г) г.
6. Если любая
точка плоскости является вектором, то, как она называется?
а) нулевой вектор;
б) равный вектор;
в) модульный вектор;
г)
точечный вектор.
7.
Определите
координаты вектора , если ![]() и
и ![]()
8.
Найдите
координаты вектора ![]() , зная координаты его начала и конца:
, зная координаты его начала и конца: ![]()
![]() .
.
9.
Найдите
длину вектора ![]() .
.
н) 25;
о) 5;
п) – 5;
р) – 25.
10.
Найдите
координаты вектора ![]() , если
, если ![]() ,
, ![]() и
и ![]() .
.
Критерии
оценивания теста
Задания
оцениваются в 1 балл в случае правильного ответа.
Отметка «отлично»
– 9-10 баллов; «хорошо» – 7-8 баллов; «удовлетворительно» – 5-6
баллов.
Ключ
к тесту
Вариант 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| б | г | г | г | а | а | (2;9) |
| в |
|
Вариант 2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| а | в | б | г | б |
| (4,3) |
| б |
|
Тесты по геометрии 9 класс. Тема: «Координаты вектора»
Правильный вариант ответа отмечен знаком +
1. Чем отличается векторная величина от скалярной?
— векторная величина может быть выражена дробным числом, а скалярная – нет
+ помимо числового значения, векторная величина характеризуется и направлением
— векторная величина обозначается двумя буквами, а скалярная – одной
— ничем не отличается
2. Дайте определение вектору:
+ отрезок, для которого известно, какая из его граничных точек является начальной, а какая конечной
— направленный отрезок с обязательной ненулевой длиной
— любой отрезок, изображенный на координатной плоскости
— прямая, совпадающая с одной и координатных осей
3. Как правильно обозначается вектор?
— двумя большими буквами, обозначающими начало и конец отрезка, со стрелкой над ними
— одной маленькой буквой со стрелкой над ней
+ оба варианта допустимы
— оба варианта неверны
4. Если начальная и конечная точка вектора совпадают, тогда:
— это не вектор, а точка на плоскости
+ это нулевой вектор
— это точка начала координат
— это единичный вектор
5. Перечислите все векторы, изображенные на картинке?
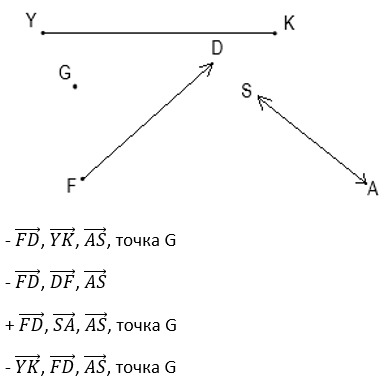
6. Что такое модуль вектора?
— величина, определяющая направление вектора
+ длина вектора, выраженная числовым значением
— четверть координатной плоскости, в которой расположен вектор
— квадратный корень из длины вектора
7. Дайте определение коллинеарным векторам:
+ векторы, отличные от нуля и находящиеся на одной либо параллельных прямых
— векторы, расположенные перпендикулярно друг другу
— векторы, расположенные в одной четверти координатной плоскости
— векторы, модули которых равны
8. Выберите фигуры, состоящие из двух пар коллинеарных векторов:
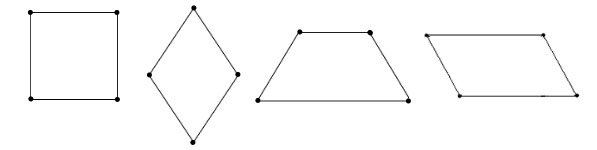
— все изображенные фигуры
+ ромб, квадрат, параллелограмм
— трапеция, квадрат, ромб
— квадрат, параллелограмм, трапеция
9. Два коллинеарных вектора имеют разное направление. Как они называются?
— сонаправленные
— разнонаправленные
+ противоположно направленные
— ненаправленные
тест 10. Свойство равных векторов заключается в том, что:
-они коллинеарны
— они сонаправлены
— их длины равны
+ они обладают всеми перечисленными свойствами
11. Вектор, длина которого равна единице, называется единичным вектором, или …. Вставьте пропущенное слово:
— квадрантом
+ ортом
— модулем
— радианом
12. При умножении вектора на число получается…Закончите утверждение:
+ вектор, коллинеарный исходному
— вектор, равный исходному
— вектор, противоположный исходному
— положительное число
13. В зависимости от того, на отрицательное или положительное число умножили вектор, получается … Закончите утверждение.
— коллинеарный или перпендикулярный вектор
— равный или противоположный вектор
+ сонаправленный или противоположно направленный вектор
— нельзя умножать вектор на отрицательное число
14. Вектор ![]() умножили на число 7. Как отличается длина получившегося вектора от исходного?
умножили на число 7. Как отличается длина получившегося вектора от исходного?
— длина исходного вектора на 7 единиц меньше
+ длина исходного вектора в 7 раз меньше
— длина исходного вектора в 1/7 раз меньше
— длина исходного вектора в 7 раз больше
15. Как называется вектор, который выходит из начала координат?
— начальный вектор
— координатный вектор
— нулевой вектор
+ радиус-вектор
16. Дан вектор ![]() с координатами {-9;5}. Разложите его по координатным векторам
с координатами {-9;5}. Разложите его по координатным векторам ![]()
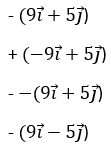
17. Чему равны координаты вектора, начало которого совпадает с началом координат?
— сумме координат начала и конца вектора
+ координатам конечной точки вектора
— произведению координат начала и конца вектора
— нулю, так как это нулевой вектор
18. На рисунке изображен вектор ![]() . Определите его правильное разложение по векторам.
. Определите его правильное разложение по векторам.
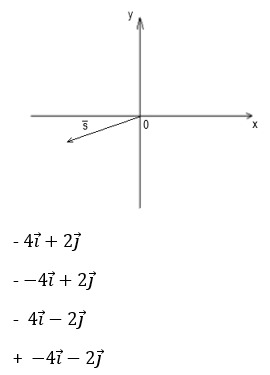
19. Как найти координаты вектора, если известны координаты точек начала и конца вектора?
— необходимо просуммировать координаты начала и конца вектора
+ необходимо от координат конца вектора отнять координаты начала вектора
— необходимо перемножить координаты начала и конца вектора
— необходимо разделить координаты конца на координаты начала вектора
тест-20. По данным на рисунке определите координаты векторов ![]()
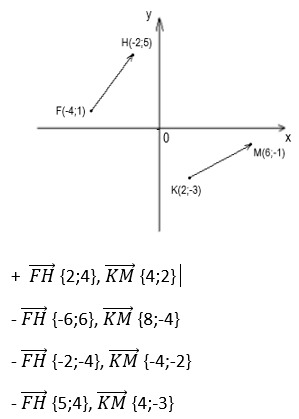
21. Известны 2 точки с их координатами: D(3;7) и K(4;-2). Какими будут векторы ![]()
— равными по длине
— противоположно направленными
— коллинеарными
+ все ответы верны
22. Чему равна каждая координата суммы векторов?
— разности соответствующих координат векторов
+ сумме соответствующих координат векторов
— произведению соответствующих координат векторов
— произведению квадратов соответствующих координат векторов
23. Даны 2 вектора ![]() Найдите координаты вектора
Найдите координаты вектора ![]()
— {-10;5}
— {10;-5}
— {-21;66}
+ {4;17}
24. Найдите координаты вектора ![]()
+ {5;5}
— {11;13}
— {-5;5}
— {11;5}
25. Модуль вектора, у которого известны координаты, равен:
— произведению координат
+ квадратному корню из суммы квадратов координат
— модулю суммы координат
— квадратному корню из произведения координат
26. Найдите длину вектора ![]() заданного своими координатами .
заданного своими координатами .
— 48
+ 10
— 4 √3
— 14
27. Как определить координаты произведения вектора на число?
— они равны квадратному корню из произведений каждой координаты на это число
— они равны произведению квадрата каждой координаты на это число
+ они равны произведению каждой координаты на это число
— они равны сумме каждой координаты с числом
28. По данным на рисунке найдите длину вектора ![]()
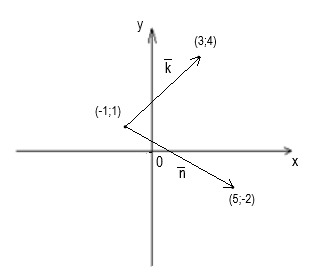
— √10
+ 2 √10
— 40
— 24
29. Дан вектор ![]() Найдите координаты вектора
Найдите координаты вектора ![]()
— {16;14}
— {54;49}
+ {63;49}
— {63;14}
тест_30. На рисунке изображены 4 точки D, K, M и R с их координатами. Вычислите координаты вектора ![]()
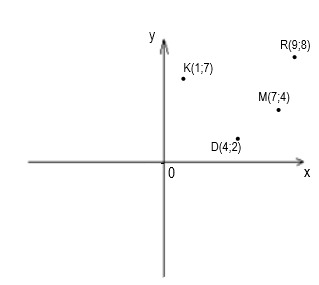
— {20;18}
+ {-18;8}
— {13;-17}
— {-19;-7}
Тест. Координаты вектора. Простейшие задачи в координатах.
Вариант I
Уровень A
1. Чему равны координаты вектора = – 3 ?
1) {0; -3};
2) {1; -3};
3) {-3; 1}.
2. Концы отрезка CD имеют координаты C (5; 1) и D (3; -7). Тогда координаты точки М – середины отрезка…
1) (8; -6);
2) (4; -4);
3) (4; -3).
3. Расстояние от начала координат до точки K (3; 4) равно…
1) 1; 2) 5; 3) 7.
4. Вектор имеет координаты {0; -1}. Его разложение по координатным векторам и …
1) = – ;
2) = — ;
3) = — .
5. Концы отрезка MN имеют координаты M (-1; 3) и N (-7; -2). Координаты вектора …
1) {-6; -5};
2) {6; 5};
3) {6; 1}.
6. Точки A и B имеют координаты: А (-3; -1) и B (2; -4). Тогда расстояние между ними равно…
1) √26; 2) 4; 3) √34.
7. Вектор {20; 15} имеет длину…
1) 35; 2) 5; 3) 25.
8. А (1; -3), В (-5; 7). Координаты вектора, равного вектору , равны…
1) {6; 10};
2) {-4; 4};
3) {-6; 10}.
9. Среди векторов {-4; 5}, {-8; -10}, {2; -2,5} укажите пару коллинеарных.
1) и ;
2) и ;
3) и .
Уровень B
1. Координаты радиус-вектора {-2; 7}.
Тогда координаты точки P равны…
2. AB – диаметр окружности. A (1; -5) и B (3; 1).
Координаты центра окружности…
3. Точка K – середина отрезка AB. A (4; 5) и K (-1; 4).
Координаты точки B…
4. Длина медианы CM треугольника ABC, вершины которого имеют координаты A (1; -4) и B (5; 2), C (0; 3), равна…
5. Вершины треугольника ABC имеют координаты: A (-5; 6), и B (3; -9), C (-12; -17).
Длины каких сторон равны?
6. ABCD – параллелограмм. B (-3; 2), C (7; -1), D (6; -5).
Координаты вершины A…
Тест. Координаты вектора. Простейшие задачи в координатах.
Вариант II
Уровень A
1. Чему равны координаты вектора = – ?
1) {-2; 0};
2) {-2; 1};
3) {-2; -1}.
2. Концы отрезка AB имеют координаты A (2; -3) и B (-4; 5). Тогда координаты точки C – середины отрезка AB…
1) (-2; 2);
2) (-1; 4);
3) (-1; 1).
3. Расстояние от точки F (5; 12) до начала координат равно…
1) 17; 2) 13; 3) 7.
4. Вектор имеет координаты {-1; 0}. Его разложение по координатным векторам и …
1) = — + ;
2) = — ;
3) = — .
5. Концы отрезка AB имеют координаты A (2; -3) и B (-3; -5). Координаты вектора …
1) {-5; -2};
2) {-1; -8};
3) {5; 2}.
6. Точки M и N имеют координаты: M (3; -2) и N (-1; 3). Тогда расстояние между ними равно…
1) 6; 2) √35; 3) √41.
7. Вектор {6; 8} имеет длину…
1) 2; 2) 14; 3) 10.
8. А (-1; 3), В (5; 7). Координаты вектора, равного вектору , равны…
1) {6; 4};
2) {4; 4};
3) {6; -4}.
9. Среди векторов {0,5; -4}, {-1; 8}, {0,25; 2} укажите пару коллинеарных.
1) и ;
2) и ;
3) и .
Уровень B
1. Координаты радиус-вектора {1; -3}.
Тогда координаты точки M равны…
2. ABCD – параллелограмм. A (-4; 3) и С (2; 5).
Диагонали параллелограмма пересекаются в точке X с координатами…
3. Точка M – середина отрезка AB. B (6; -3) и M (1; -4).
Координаты точки A равны…
4. Длина медианы AM треугольника ABC, вершины которого имеют координаты A (0; 1) и B (1; -4), C (5; 2), равна…
5. Вершины треугольника ABC имеют координаты: A (4; 8), B (12; 5), C (7; 0).
Длины каких сторон равны?
6. ABCD – параллелограмм. A (-3; -1), B (-2; 4), C (6; -1).
Координаты вершины D…



 .
. . В ответе укажите координаты вектора по образцу {1;-5;3,5} без пробелов.
. В ответе укажите координаты вектора по образцу {1;-5;3,5} без пробелов.

 …
… {6; 8} имеет длину…
{6; 8} имеет длину… {0,25; 2} укажите пару коллинеарных.
{0,25; 2} укажите пару коллинеарных. {1; -3}.
{1; -3}.