Контрольная работа № 2 по математике 6 класс с ответами (УМК Виленкин) Вариант 1. Задания: Сократи. Выполни действия. Реши уравнение. Какую часть всего пути турист прошел за эти двое суток? Найди четыре дроби, каждая из которых больше … и меньше … Математика 6 Виленкин Контрольная 2 В1 + ОТВЕТЫ.
Другие варианты: КР-02. Вариант 2 КР-02. Вариант 3 КР-02. Вариант 4
К-02. Вариант 1 (транскрипт заданий)
- Сократи: 8/14; 7/63; 30/84; (34•12)/(3•7).
- Выполни действия: а) 3/7 + 5/14; б) 8/9 – 7/12; в) 11/50 – 3/25 + 1/20.
- Реши уравнение: а) 11/12 – y = 11/24; б) 5,86m + 1,4m = 76,23.
- В первые сутки теплоход прошел 9/20 всего пути, во вторые сутки – на 1/15 пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?
- Найди четыре дроби, каждая из которых больше 5/9 и меньше 7/9.
Математика 6 Виленкин Контрольная 2 В1
РЕШЕНИЯ и ОТВЕТЫ:
КР-02. Вопросы и ответы на Вариант 1
Вопрос № 1. Сократи: 8/14; 7/63; 30/84; (34 • 12) / (3 • 7).
ОТВЕТ: 8/14 = 4/7; 7/63 = 1/9; 30/84 = 5/14; (34•12)/(3•7) = 136/7.
Вопрос № 2. Выполни действия: а) 3/7 + 5/14; б) 8/9 – 7/12; в) 11/50 – 3/25 + 1/20.
ОТВЕТ: а) 11/14; б) 11/36; в) 3/20.
Вопрос № 3. Реши уравнение: а) 11/12 – y = 11/24; б) 5,86m + 1,4m = 76,23.
ОТВЕТ: а) у = 11/24; б) m = 10,5.
Вопрос № 4. В первые сутки теплоход прошел 9/20 всего пути, во вторые сутки – на 1/15 пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?
ОТВЕТ: 29/30 пути.
Вопрос № 5. Найди четыре дроби, каждая из которых больше 5/9 и меньше 7/9.
Указание к решению: 15/27 < x < 21/27.
ОТВЕТ, например, может быть таким: 16/27; 17/27; 18/27; 19/27. Есть и другие варианты ответа.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЯ
Другие варианты: КР-02. Вариант 2 КР-02. Вариант 3 КР-02. Вариант 4
Вы смотрели: Контрольная работа № 2 по математике в 6 классе с ответами (для УМК Виленкин и др.) Вариант 1. Цитаты из пособия «Математика. 6 класс. Контрольные работы / В.И. Жохов, Л.Б. Крайнева. — М.: Мнемозина» использованы в учебных целях. Математика 6 Виленкин Контрольная 2 В1 + ОТВЕТЫ.
Вернуться в меню: Список контрольных работ (Оглавление)
Математика 6 Никольский К-2 В-1 с ответами. Контрольная работа № 2 по математике 6 класс (вариант 1): задания, решения и ответы. Представленные ниже контрольная работа ориентирована на УМК Никольский (МГУ — школе). Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий.
Другие варианты: К-2 Вариант 2 К-2 Вариант 3 К-2 Вариант 4
К-2. Вариант 1 (транскрипт заданий)
- Начертите отрезок АВ, длина которого равна 8 см. Постройте:
а) отрезок MN, длина которого составляет 25 % длины отрезка АВ;
б) отрезок XY, длина которого составляет 150 % длины отрезка АВ. - Вычислите 20 % числа 35.
- Было 500 р. Потратили 40 % всей суммы и 50 остатка. Сколько денег осталось?
- За контрольную работу учащиеся 8 класса получи 4 отметки «5», 10 отметок «4», 10 отметок «3». Других отметок не было. Постройте круговую диаграмму по этим данным.
- Товар стоил 400 р. Определите его цену после двух повышений цены – сначала на 20 %, потом на 10%.
Математика 6 Никольский К-2 В-1 ОТВЕТЫ
Ответы на Вариант 1:
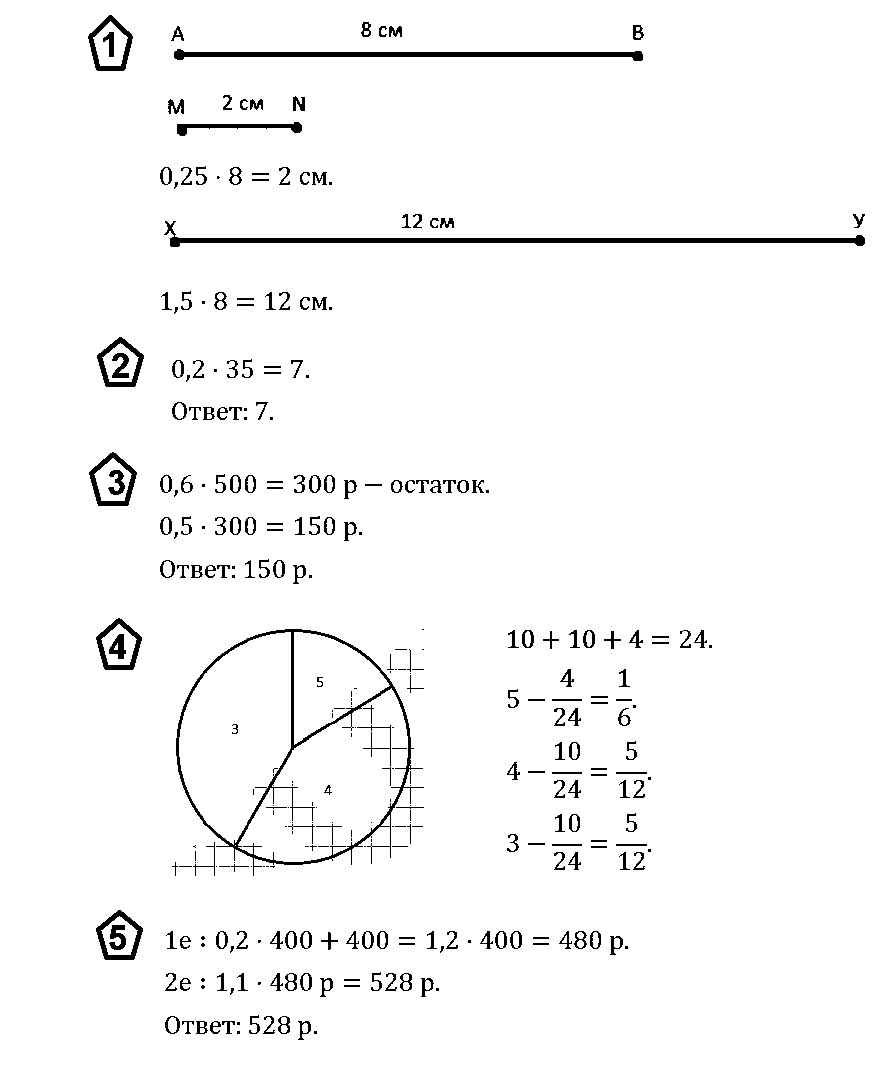
№ 1. Начертите отрезок АВ, длина которого равна 8 см. Постройте:
а) отрезок MN, длина которого составляет 25 % длины отрезка АВ;
б) отрезок XY, длина которого составляет 150 % длины отрезка АВ.
Правильный ОТВЕТ: a) MN = 2 см; б) ХY =12 см.
№ 2. Вычислите 20 % числа 35.
Правильный ОТВЕТ: 7.
№ 3. Было 500 р. Потратили 40 % всей суммы и 50 остатка. Сколько денег осталось?
Правильный ОТВЕТ: 150 р.
№ 4. За контрольную работу учащиеся 8 класса получи 4 отметки «5», 10 отметок «4», 10 отметок «3». Других отметок не было. Постройте круговую диаграмму по этим данным.
Правильный ОТВЕТ смотри в спойлере (ниже).
№ 5. Товар стоил 400 р. Определите его цену после двух повышений цены – сначала на 20 %, потом на 10%.
Правильный ОТВЕТ: 528 р.
♦ Нажмите на спойлер ниже, чтобы увидеть решения всех заданий.
Смотреть РЕШЕНИЯ заданий Варианта 1
Другие варианты: К-2 Вариант 2 К-2 Вариант 3 К-2 Вариант 4
Вернуться к Списку контрольных работ по математике в 6 классе (Никольский)
Математика 6 Никольский К-2 В-1. Цитаты из пособия «Математика. Дидактические материалы 6 класс / Потапов, Шевкин» использованы в учебных целях, а также для ознакомления и покупки учебного пособия. Контрольная работа № 2 по математике в 6 классе для УМК Никольский с ОТВЕТАМИ.
- Категория: ГДЗ Математика 6 класс дидактические материалы Мерзляк. Контрольные и самостоятельные работы с ответами ✔
Мы помним из четвертого класса, что сравнивать, складывать и вычитать можно только дроби с одинаковыми знаменателями. А чтобы привести дроби наименьшему к одинаковому знаменателю, нужно найти их НОК. Дальше все просто. При сравнении сравниваем только числители. При сложении или вычитание производим действие так же только с числителями, а знаменатель оставляем тем же.
-
Вариант 1
-
Вариант 1
1. Сократите дробь:
1) 12/16; 2) 18/27Ответ:
1) $frac{12}{16}=frac34$
2) $frac{18}{27}=frac23$
2. Сравните дроби:
1) 5/8 и 3/4; 2) 4/9 и 3/8Ответ:
1) $frac58<frac34$
$frac{3^{(2}}4=frac68$
$frac58<frac68$2) $frac49>frac38$
$frac{4^{(8}}9=frac{32}{72}$
$frac{3^{(9}}8=frac{27}{72}$
$frac{32}{72}>frac{27}{72}$3. Вычислите:
1) 4/15 + 3/4; 2) 5/6 – 9/14; 3) 4 4/7 + 6 1/4; 4) 5 7/8 – 3 5/6.Ответы:
1) $frac{4^{(4}}{15}+frac{3^{(15}}4=frac{16}{60}+frac{45}{60}=frac{16+45}{60}=frac{61}{60}=1frac1{60}$
2) $frac{5^{(7}}6-frac{9^{(3}}{14}=frac{35}{42}+frac{27}{42}=frac{35+27}{42}=frac8{42}=frac4{21}$
3) $4frac{4^{(4}}7+6frac{1^{(7}}4=4frac{16}{28}+6frac7{28}=10frac{23}{28}$
4) $5frac{7^{(3}}8-3frac{5^{(7}}6=5frac{21}{24}-3frac{20}{24}=2frac1{24}$
4. В первый день продали 4 7/24 ц картофеля, а во второй – на 1 7/12 ц меньше. Сколько центнеров картофеля продали за два дня?
1) $4frac7{24}-1frac{7^{(2}}{12}=3frac{31}{24}-1frac{14}{24}=2frac{17}{24}$ (ц) — картофеля продали за второй день
2) $4frac7{24}+2frac{17}{12}=6frac{24}{24}=7$ (ц) — картофеля продали за два дня
Ответ: 7 ц картофеля.5. Решите уравнение:
1) 10 11/24 – х = 6 7/16; 2) (5/6 + х) – 2/3 = 13/181) $10frac{11}{24}-х=6frac7{16}$
$х=10frac{11^{(2}}{24}-6frac{7^{(3}}{16}$
$х=10frac{22}{48}-6frac{21}{48}$
$х=4frac1{48}$2) $(frac56+х)-frac23=frac{13}{18}$
$frac56+х=frac{13}{18}+frac{2^{(6}}3$
$frac56+х=frac{13}{18}+frac{12}{18}$
$х=frac{25}{18}-frac{5^{(3}}6$
$х=frac{25}{18}-frac{15}{18}$
$х=frac{10}{18}=frac59$6. За первый день турист прошёл 5/18 туристического маршрута, за второй – 7/27, за третий – 2/9. Оставшуюся часть маршрута он прошёл за четвёртый день. Какую часть маршрута прошёл турист за четвёртый день?
1) $frac{5^{(3}}{18}+frac{7^{(2}}{27}+frac{2^{(6}}9=frac{15+14+12}{54}=frac{41}{54}$ (часть) — маршрута прошел турист за три дня
2) $1-frac{41}{54}=frac{54-41}{54}=frac{13}{54}$ (части) — прошел турист за четвертый день
Ответ: 13/54 маршрута.7. Найдите все натуральные значения х, при которых верно неравенство х/9 < 22/45.
$frac х9<frac{22}{45}$
$frac{5х}{45}<frac{22}{45}$
5х<22
х < 22 : 5
х < 4,4
х — натуральное число.
х = {1, 2, 3, 4}. -
Вариант 2
-
Вариант 2
1. Сократите дробь:
1) 12/15; 2) 14/21.Ответ:
1) $frac{12}{15}=frac45$
2) $frac{14}{21}=frac23$2. Сравните дроби:
1) 9/10 и 4/5; 2) 4/7 и 2/3.Ответы:
1) $frac9{10}>frac45$
$frac{4^{(2}}5=frac8{10}$
$frac9{10}>frac8{10}$2) $frac47<frac23$
$frac{4^{(3}}7=frac{12}{21}$
$frac{2^{(7}}3=frac{14}{21}$
$frac{12}{21}<frac{14}{21}$3. Вычислите:
1) 4/7 + 2/5; 2) 7/12 – 5/9; 3) 2 3/4 + 3 2/5; 4) 3 4/9 – 2 1/6.1) $frac{;;4^{(5}}7+frac{;;2^{(7}}5=frac{20}{35}+frac{14}{35}=frac{20+14}{35}=frac{34}{35}$
2) $frac{;;7^{(3}}{12}-frac{;;5^{(4}}9=frac{21}{36}-frac{20}{36}=frac{21-20}{36}=frac1{36}$
3) $2frac{;;3^{(5}}4+3frac{;;;2^{(4}}5=2frac{15}{20}+3frac8{20}=5frac{23}{20}=6frac3{20}$
4) $3frac{;;4^{(5}}9-2frac{;;;1^{(3}}6=3frac8{18}-2frac3{18}=1frac5{18}$
4. На путь из пункта А в пункт В велосипедист потратил 3 1/6 ч, а на путь из пункта В в пункт С – на 1 1/3 ч меньше. Сколько часов потратил велосипедист на путь из пункта А в пункт С?
1) $3frac16-1frac{;;1^{(2}}3=2frac76-1frac26=1frac56$ (ч.) — потратил велосипедист из пункта В в пункт С
2) $3frac16+1frac56=4frac66=5$ (ч.) — потратил велосипедист на путь из пункта А в пункт С
Ответ: 5 ч.5. Решите уравнение:
1) 8 9/10 – х = 4 5/6; 2) 9/14 + (х – 3/7) = 23/28.1) $8frac9{10}-х=4frac56$
$х=8frac{9^{(3}}{10}-4frac{5^{(5}}6$
$х=8frac{27}{30}-4frac{25}{30}$
$х=4frac2{30}=4frac1{15}$2) $frac9{14}+(х-frac37)=frac{23}{28}$
$х-frac37=frac{23}{28}-frac{9^{(2}}{14}$
$х-frac37=frac{23}{28}-frac{18}{28}$
$х=frac5{28}+frac{3^{(4}}7$
$х=frac5{28}+frac{12}{28}$
$х=frac{17}{28}$6. За первую неделю отремонтировали 1/8 дороги, за вторую – 5/12, за третью – 3/16. Оставшуюся часть дороги отремонтировали за четвёртую неделю. Какую часть дороги отремонтировали за четвёртую неделю?
1) $frac{1^{(6}}8+frac{5^{(4}}{12}+frac{3^{(3}}{16}=frac{6+20+9}{48}=frac{35}{48}$ (дороги) — отремонтировали за 3 недели
2) $1-frac{35}{48}=frac{48-35}{48}=frac{13}{48}$ (дороги) — отремонтировали за четвёртую неделю.
Ответ: 13/18 дороги.7. Найдите все натуральные значениях, при которых верно неравенство х/8 < 31/48.
$frac х8<frac{31}{48}$
$frac{6х}{48}<frac{31}{48}$
6х < 31
$х<frac{31}6$
$х<5frac16$
х — натуральное число
х = {1, 2, 3, 4, 5}.




 Мы помним из четвертого класса, что сравнивать, складывать и вычитать можно только дроби с одинаковыми знаменателями. А чтобы привести дроби наименьшему к одинаковому знаменателю, нужно найти их НОК. Дальше все просто. При сравнении сравниваем только числители. При сложении или вычитание производим действие так же только с числителями, а знаменатель оставляем тем же.
Мы помним из четвертого класса, что сравнивать, складывать и вычитать можно только дроби с одинаковыми знаменателями. А чтобы привести дроби наименьшему к одинаковому знаменателю, нужно найти их НОК. Дальше все просто. При сравнении сравниваем только числители. При сложении или вычитание производим действие так же только с числителями, а знаменатель оставляем тем же.