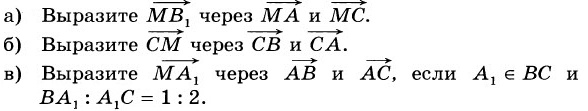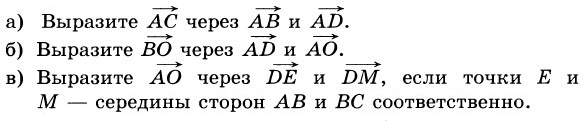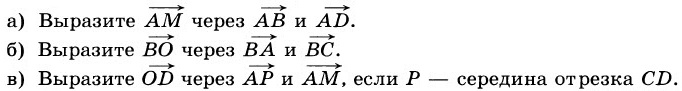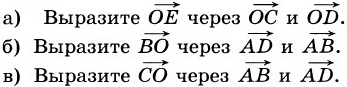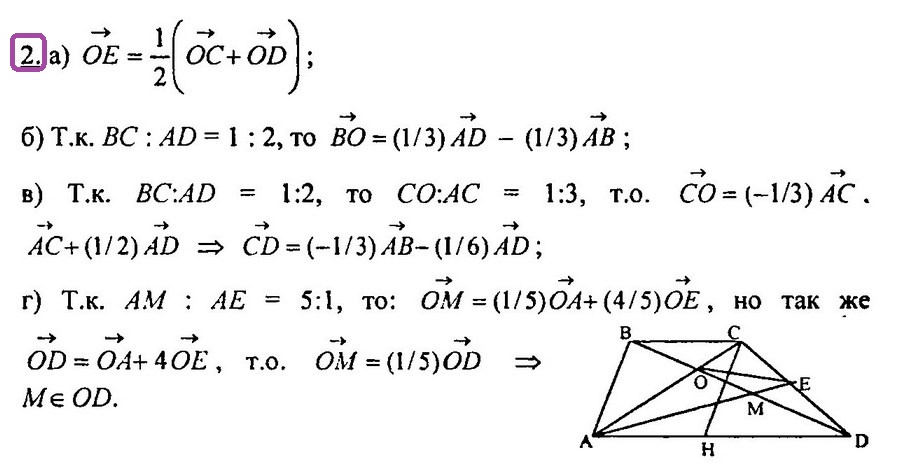Контрольная работа по геометрии «Векторы» (8 класс)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 6 «Векторы» (в 4-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Геометрия 8 класс (УМК Атанасян и др.)
Контрольная работа № 6 «Векторы».
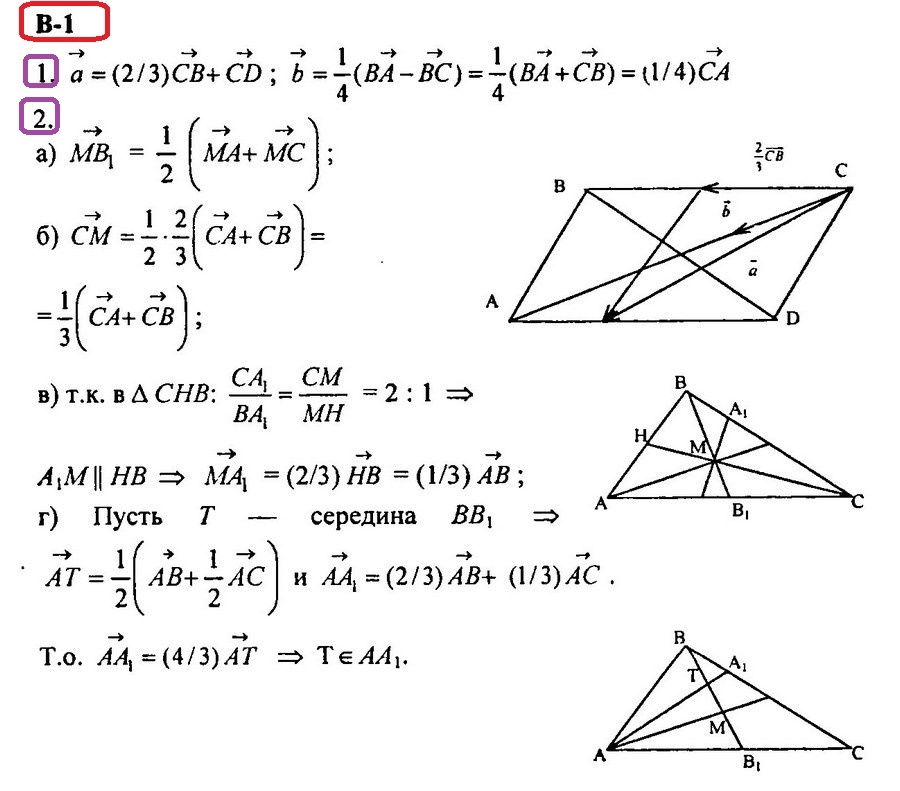
К–6 Вариант 1
1. Начертите параллелограмм ABCD и постройте векторы .
2. В треугольнике АВС В1 – середина АС, М – точка пересечения медиан.
г)* Используя векторы, покажите, что середина отрезка ВВ1 лежит на прямой АА1, если А1 ∈ ВС и ВА1 : А1С = 1 : 2.
К–6 Вариант 2
1. Начертите два неколлинеарных вектора а̅ и b̅, отложенных от разных точек. Постройте векторы
2. В трапеции ABCD основания AD и ВС относятся как 3 : 1. Диагонали трапеции пересекаются в точке О.
г)* Докажите, что DE < (2/3 DA + 1/2 DC), если точка Е – середина стороны АВ.
К–6 Вариант 3
1. Начертите треугольник АВС и постройте векторы
2. В параллелограмме ABCD точка М – середина стороны ВС, отрезки BD и AM пересекаются в точке О.
г)* Докажите, что OP < (2/3 AD + 1/6 АВ), если Р – середина отрезка CD.
К–6 Вариант 4
1. Начертите два неколлинеарных вектора а̅ и b̅, отложенных от разных точек. Постройте векторы
2. Основания ВС и АВ трапеции ABCD относятся как 1 : 2, Е – середина стороны CD, О – точка пересечения диагоналей.
г)* Используя векторы, докажите, что точка М, делящая отрезок АЕ в отношении 1 : 4, считая от точки Е, принадлежит прямой BD.
Геометрия 8 класс (УМК Атанасян и др.)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 6 «Векторы» (в 4-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Контрольные работы по геометрии 9 класс с ответами для УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 9 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». Ответы адресованы родителям. Геометрия 9 Контрольные работы Атанасян + Ответы.
Геометрия 9 класс. Контрольные работы
по учебнику Атанасяна
ГЛАВА IX. ВЕКТОРЫ
Урок 14. Контрольная работа № 1 по геометрии с ответами по теме «Векторы»:
К-1 Уровень 1 (легкий)
К-1 Уровень 2 (средний)
К-1 Уровень 3 (сложный)
ГЛАВА Х. МЕТОД КООРДИНАТ
Урок 24. Контрольная работа № 2 по геометрии с ответами по теме «Метод координат» (3 уровня):
К-2 Уровень 1 (легкий)
К-2 Уровень 2 (средний)
К-2 Уровень 3 (сложный)
ГЛАВА XI. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Урок 38. Контрольная работа № 3 по геометрии с ответами по теме «Соотношение между сторонами и углами треугольника. Скалярное произведение векторов» (3 уровня):
К-3 Уровень 1 (легкий)
К-3 Уровень 2 (средний)
К-3 Уровень 3 (сложный)
ГЛАВА XII. ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
Урок 50. Контрольная работа № 4 по геометрии с ответами по теме «Длина окружности и площадь круга» (3 уровня):
К-4 Уровень 1 (легкий)
К-4 Уровень 2 (средний)
К-4 Уровень 3 (сложный)
ГЛАВА XIII. ДВИЖЕНИЯ
Урок 59. Контрольная работа % 5 по геометрии (нет ответов) по теме «Движения» (3 уровня):
Контрольная работа № 5
ИТОГОВОЕ ПОВТОРЕНИЕ
Урок 70. «Итоговая контрольная работа» за курс 9 класса с ответами (один уровень, 2 варианта)
Итоговая контрольная работа + Ответы
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
Смотрите также: ВСЕ КОНТРОЛЬНЫЕ РАБОТЫ в 9 классе
Вы смотрели: Геометрия 9 Контрольные работы Атанасян — контрольные работы по геометрии в 9 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 9 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Контрольные работы других авторов и УМК (с ответами):
УМК МЕРЗЛЯК: Дидактические материалы 9 класс (6 контрольных по 2 варианта)
УМК АТАНАСЯН: Мельникова. Контрольные работы по геометрии 9 кл. (7 работ)
УМК АТАНАСЯН: Геометрия 9 класс УЧЕБНИК (задачи из учебника с ответами)
УМК БУТУЗОВ: Дидактические материалы (контрольные работы и матем. диктанты)
УМК ПОГОРЕЛОВ: Гусев. Дидактические материалы — Контрольные работы для 9кл.
Геометрия 11 Атанасян Контрольная 6
Контрольная работа № 6 по геометрии в 11 классе с ответами «Метод координат в пространстве. Скалярное произведение векторов» по УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Геометрия 11 Атанасян Контрольная 6.
Геометрия 11 класс (УМК Атанасян)
Контрольная работа № 6 (авт. Иченская)
К-6. Вариант 1
- Даны векторы а{1; –2; 0}, b{3; –6; 0}, с{0; –3; 4}. Найдите координаты вектора р = 2а – b/3 – с.
- Найдите угол между прямыми АВ и CD, если А(6; –4; 8), В(8; –2; 4), С(12; –6; 4), D(14; –6; 2).
- Дан куб ABCDA1B1C1D1. Найдите угол φ между векторами AD1 и ВМ, где М – середина ребра DD1.
К-6. Вариант 2
- Даны векторы a = 2i – 3j + k и b = 4i – 2k, где i, j, k – единичные взаимно перпендикулярные векторы (орты). Найдите скалярное произведение векторов а и b.
- Найдите угол между прямыми MN и EF, если М(1; 1; 0), N(3; –1; 0), E(4; –1; 2), F(0; 1; 0).
- Даны координаты вершин тетраэдра МАВС: М(2; 5; 7), А(1; –3; 2), В(2; 3; 7), С(3; 6; 0). Найдите расстояние от точки К до точки О, где K – середина ребра AM, О – середина ребра ВС.
Смотреть графический вид контрольной (Варианты 1, 2)

К-6. Вариант 3
- Даны векторы а{2; 4; –6}, b{–3; 1; 0}, с{3; 0; –1}. Найдите координаты вектора р = –а/2 + 2b – с.
- Найдите угол между прямыми АВ и CD, если A(√3; 1; 0), В(0; 0; 2√2), С(0; 2; 0), D(√3; 1; 2√2).
- Дан куб ABCDA1B1C1D1. Найдите угол между векторами АС и C1D.
К-6. Вариант 4
- Даны векторы a = 5i – 2j + 4k и b = 3j + 2k, где i, j, k – единичные взаимно перпендикулярные векторы (орты). Найдите скалярное произведение векторов а и b.
- Найдите угол между прямыми MN и КЕ, если М(2; 0; 0), N(0; 2; 0), K(2; 2; 0), E(2; 2; 2).
- В прямоугольном параллелепипеде ABCDA1B1C1D1 точка М – центр грани AA1D1D. Найдите угол φ между векторами ВМ и В1С, если измерения параллелепипеда АВ = 4 м, AD = 3 м, AA1 = 5 м.
Смотреть графический вид контрольной (Варианты 3, 4)

Ответы на контрольную работу

Вернуться к Списку контрольных работ по геометрии в 11 классе (Атанасян)
Вы смотрели: Контрольная работа по геометрии 11 класс «Метод координат в пространстве. Скалярное произведение векторов» с ответами для УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : базовый уровень / Иченская» использованы в учебных целях. Геометрия 11 Атанасян Контрольная 6 + Ответы.
Контрольная работа № 1. Векторы
1 вариант.
1. Начертите два неколлинеарных вектора и . Постройте векторы, равные:
а) ; б)
2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и .
3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и .
2 вариант
1. Начертите два неколлинеарных вектора и . Постройте векторы, равные:
а) ; б)
2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и
3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.
4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k.
Контрольная работа № 2. Метод координат.
1 вариант.
1. Найдите координаты и длину вектора , если .
2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2).
3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2).
а) Докажите, что Δ— равнобедренный;
б) Найдите высоту, проведённую из вершины М.
4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ).
2 вариант.
1). Найдите координаты и длину вектора , если .
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2).
а) Докажите, что Δ— равнобедренный;
б) Найдите биссектрису, проведённую из вершины С.
4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ).
Контрольная работа № 3.
Соотношения между сторонами и углами треугольника.
1 вариант
- В треугольнике АВС А = 450,
В = 600, ВС = Найдите АС.
- Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
- Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
- * В ΔАВС АВ = ВС, САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
2 вариант
- В треугольнике СDEС = 300,
D = 450, СЕ =Найдите DE.
- Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
- Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
- * В ромбе АВСD АК – биссектриса угла САВ, ВАD = 600, ВК = 12 см. Найдите площадь ромба.
Контрольная работа № 4.
Длина окружности и площадь круга.
1 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна
2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности.
2 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
Контрольная работа № 5.
Движения.
1 вариант
1. Начертите ромб АВСD. Постройте образ этого ромба:
а) при симметрии относительно точки С;
б) при симметрии относительно прямой АВ;
в) при параллельном переносе на вектор ;
г) при повороте вокруг точки D на 600 по часовой стрелке.
2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
2 вариант
1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:
а) при симметрии относительно точки D;
б) при симметрии относительно прямой CD;
в) при параллельном переносе на вектор ;
г) при повороте вокруг точки А на 450 против часовой стрелки.
2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.