Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
Страница 1 из 2
-
- Регистрация:
- 3 мар 2011
- Сообщения:
- 2
- Симпатии:
- 0
- Адрес:
-
Москва
Всем Привет, помогите если можете.
Проблема следующая: есть документ, в котором есть координаты пунктов триангуляции по 2 объектам: 1: 6465252.63, 8311157.56 и 2: 424551.30, -18532.02 (СК63 для 1 точно 2 я так думаю).
Работаю в ГеоКаде, 1 без проблем пересчитал (есть самодельная прога МСК и СК42), а с 2 не могу понять, как водить координаты (т.е. синтаксис) для 1 было так: 6465252.63, -11157.56 со 2 вариантом не работает. Думаю проблема в том, что в первых зоны разные 1 вариант 20 зона а 2 вар. 21 (это я если СК42) и как следствие меридиан другой нужно устанавливать. Я по образованию не геодезист так в институте общий курс проходил. Заранее благодарен за внимание к моей проблеме.#1
-
Форумчанин
- Регистрация:
- 15 фев 2008
- Сообщения:
- 218
- Симпатии:
- 13
- Адрес:
-
Краснодар
Вторая точка — не понятно в какой системе координат.
В документе, из которого вы взяли координаты, разве не указано в какой именно системе приведены координаты?#2
-
- Регистрация:
- 3 мар 2011
- Сообщения:
- 2
- Симпатии:
- 0
- Адрес:
-
Москва
Там просто написано «Система координат местная», но учытывая что это документы схожих объектов и делались в одно время 1970-1980 гг и одной конторой чувство у меня что там и там СК63. Просто первые цифры убраны кстати в первом документе на других точтах тоже убраны первые цифры на Y но так как координаты триан. пунктов даны полностью то я их определил. А в 2 варианте первых цифр нет и так как это другая зона (СК42) то я предпологаю что они другие и меридиан при пересчете другой. Вот и ищу подсказку как СК 63 по зонам отличается.
(Добавление)
кстати что в 2 варианте в X первая цифра 6 точно так как объекты по X на одном уровне(2 северне 1 на 100 км) а вот по Y между ними 360км (2 западнее 1) блин а может и не 6 эта цифра
(Добавление)
СОРРИ перепутал:
кстати что в 2 варианте в X первая цифра 6 точно так как объекты по X на одном уровне(2 южнее 1 на 100 км) а вот по Y между ними 360км (2 восточнее 1) блин а может и не 6 эта цифра.#3
-
Форумчанин
- Регистрация:
- 15 фев 2008
- Сообщения:
- 218
- Симпатии:
- 13
- Адрес:
-
Краснодар
Сложно что-то посоветовать. Не сталкивался я с Якутией.
Выкладываю картинку со схемой СК-63, она висит в какой-то из ранних тем форума,
возможно, что-то вам даст.
Ну и ссылка на параметры некоторых зон СК-63.
http://system-1963.narod.ru/Вложения:
#4
-
Форумчанин
Как понять «пересчитал без проблем»? Если предположить, что для точки 1 указаны в СК42 преобразованные координаты, то Y(непреобразованный) = -188841.44, а не -11157.56, как указано у вас. Вообще-то ни одна система координат, (кроме местной, неудачно спроектированной) не использует отрицательных координат.
Это где?
Почему, если вы испрашивая у людей совета и помощи, не потрудились перечитать свое послание, прежде чем нажать «Enter»? «СК63 для 1 точно 2 я так думаю»??? Это же какое-то бессвязное бормотание, а не вопрос!#5
-
Форумчанин
- Регистрация:
- 17 фев 2009
- Сообщения:
- 77
- Симпатии:
- 4
- Адрес:
-
Татарстан
Здравствуйте всем! А есть ли такая же схема для СК-42?
#6
-

Форумчанин
Если Вам нужно определить номер 6-градусной зоны в проекции ГК, то это можно сделать по известной долготе точки (меридиану):
N = (L+3)/6, где
N — номер зоны;
L — осевой меридиан зоны.
Например, точка с имеет геодезические координаты 46г20м и 47г00м (взяты с навигатора), тогда номер зоны будет 8.#7
-

Команда форума
Форумчанин- Регистрация:
- 18 май 2007
- Сообщения:
- 21.012
- Симпатии:
- 6.661
- Адрес:
-
Россия
— а смысл? Там же все просто))
#8
-

Форумчанин
Да есть такая схема для 42го. Географическая карта называется.
#9
-
Форумчанин
- Регистрация:
- 17 фев 2009
- Сообщения:
- 77
- Симпатии:
- 4
- Адрес:
-
Татарстан
surveyorX-Y-HСпасибо.
OhrДа точно. Спасибо#10
-

Форумчанин
- Регистрация:
- 10 дек 2008
- Сообщения:
- 54
- Симпатии:
- 7
- Адрес:
-
ХМАО Югорск
Хорошо выложили. Только вот не понятно, как можно определить номер зоны в системе СК-63 зная долготу/широту?
(Добавление)может быть выложите картограмму в исходном формате с которого делался JPG, тогда и вопросы сами собой все пропадут?
#11
-

Форумчанин
- Регистрация:
- 11 июн 2009
- Сообщения:
- 1.974
- Симпатии:
- 474
posttempuser
ЦМ в таблице это долгота осевого меридиана. Номер зоны определяешь по таблице!#12
-

- Регистрация:
- 16 июл 2009
- Сообщения:
- 7
- Симпатии:
- 1
- Адрес:
-
Екатеринбург
Может есть у кого параметры СК 1963 года, района Q ?!!
#13
-

Форумчанин
- Регистрация:
- 26 мар 2009
- Сообщения:
- 2.456
- Симпатии:
- 1.037
- Адрес:
-
Киев
Да, есть. Называется » Бланковая карта СССР 1:1 000 000 «
Можно найти в интернете.#14
-

Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.683
- Симпатии:
- 4.639
Может, у кого-то и есть. Как Вы думаете, он должен подставлять форум и разглашать в открытую секретные данные?
#15
-

- Регистрация:
- 16 июл 2009
- Сообщения:
- 7
- Симпатии:
- 1
- Адрес:
-
Екатеринбург
http://system-1963.narod.ru/ — ранее эту ссылку выложили, там есть параметры большинства районов, но нет района Q. Парадокс в том, что все это секретно, но правильному без параметров не посчитать
#16
-

Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.683
- Симпатии:
- 4.639
В таком случае:
1. Официально получают.
2. Неофициально покупают.
3. Публикуют, но не на тех форумах, которые уважают Законы государства.
4. Делятся между собой в личной переписке.#17
-

Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.535
- Симпатии:
- 4.969
Не могу сказать по остальные, но для района L в ссылке даны неверные значения осевых меридианов зон.
#18
-

Форумчанин
- Регистрация:
- 27 май 2009
- Сообщения:
- 62
- Симпатии:
- 3
- Адрес:
-
Юг России
Уважаемые, нет ли среди Вас тех, кто желает пообщаться со мной в личке на счёт ск63 р-он»T». Буду очень признателен!!!! ::write::
#19
-

Форумчанин
А можно поподробнее ? Где можно увидеть таблицу эту ?
#20
Страница 1 из 2
Поделиться этой страницей
сдвоенными по долготе, а севернее параллели 76о (до 88о) – счетверенными по долготе. На участках (на севере и юге) по широтам от 88о до 90о находятся полярные шапки, которые изображают в азимутальной проекции. Вид такой проекции представлен на рис. 2.2.
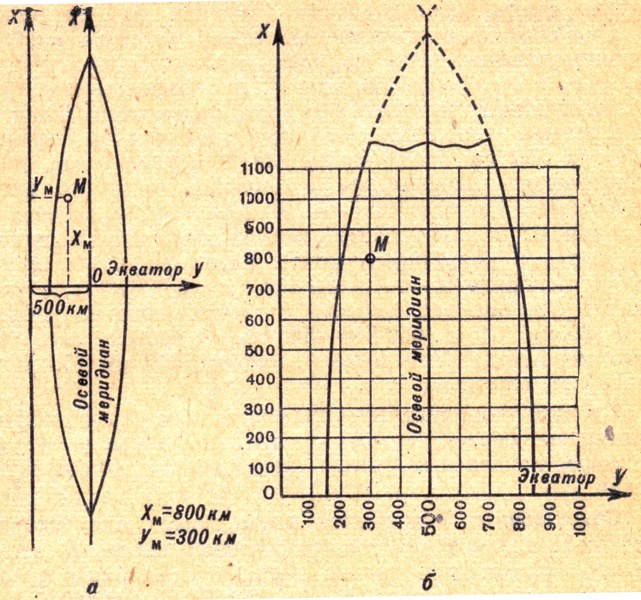
Как уже указывалось в § 10, поверхность земного эллипсоида изображают на плоскости в проекции Гаусса-Крюгера в пределах 6о (или 3о) зон. Проекции осевого меридиана зоны и экватора образуют на плоскости две взаимно перпендикулярные линии, которые и принимают в качестве осей х и у прямоугольных координат. Осью х является проекция осевого меридиана зоны, а осью у – проекция экватора (рис. 2.13). В каждой из зон образуется
| своя отдельная система прямоугольных координат. | ||
| Для территории России абсциссы х | ||
| всех точек положительные, а ординаты у | ||
| могут быть положительными и отрица- | ||
| тельными. Для удобства в работе ось х | ||
| вынесли за пределы зоны на запад на | ||
| 500 км, т.е. сделали ординаты всех точек | ||
| зоны положительными. | ||
| Таким образом, положение любой точ- | ||
| ки в зоне определяется координатой х (рас- | ||
| стоянием до точки от экватора) и коорди- | ||
| Рис. 2.13. Зональная система | натой у, определяемой расстоянием от вы- | |
| несенного на запад осевого меридиана (оси | ||
| прямоугольных координат | х) до точки при перемещении на восток. | |
| Координата у взаимосвязана с расстоянием y(L) от точки до осевого | ||
| меридиана зоны следующим соотношением: | ||
| y = 500 км + y(L) . | (2.8) |
При этом следует иметь ввиду, что значение y(L) может быть отрицательным, когда точка находится в западной от осевого меридиана части зоны (у < 500 км), и положительным, если точка находится в восточной части зоны (у > 500 км). Величины y(L) называют действительными значениями ординат в зоне, а значения у – преобразованными ординатами.
Поскольку системы прямоугольных координат подобны для каждой зоны, то необходимо ввести параметр для различения двух точек А и В, имеющих одинаковые координаты х и у(L), но находящихся в разных зонах. Для этого впереди координаты у приписывают номер зоны.
Пример 2.3. Точка находится на расстоянии 5237,635 км от экватора и на расстоянии 105,842 км к западу от осевого меридиана 7-й зоны. Записать прямоугольные координаты точки.
Решение. Координатой х будет указанное расстояние точки от экватора – 5237,635 км. Поскольку L = — 105,842 км (западная часть зоны), то, пользуясь формулой (2.8), получим у = 500,000 км – 105,842 км = 394,158 км (7-я зона). Следовательно:
30
х = 5 237,635 км; у = 7 394,158 км Для того, чтобы определить номер зоны по координате у, необходимо от запятой,
отделяющей целые километры, отсчитать влево три значащих цифры. Остаток будет номером зоны.
Пример 2.4. у = 16 636 835 м = 16 636, 835 км → 16-я зона.
y(L) = 636,835 км – 500,000 км = + 136,835 км (восточная часть зоны).
§ 13. Перевычисление координат из зоны в зону
Поскольку в каждой из зон существует своя отдельная система прямоугольных координат, то часто, при переходе из зоны в зону (при продвижении инженерных работ) возникает необходимость перевычисления координат, например, из зоны n в зону (n+1) или в зону (n-1).
Предположим, что некоторая точка А имеет геодезические координаты ВА (геодезическую широту) и LА (геодезическую долготу). Поскольку разность долгот граничных меридианов зоны равна 6о, то соответственно для каждой из зон можно получить долготы крайних меридианов: 1-я зона (0о – 6о), 2-я зона (6о – 12о), 3-я зона (12о – 18о) и т.д. Таким образом, по геодезической долготе точки А можно определить номер зоны, в которой эта точка находится. При этом долгота осевого меридиана зоны определится по формуле (2.7): Lо = (6оn – 3о), в которой n – номер зоны.
Для определения плоских прямоугольных координат х и у по геодезическим координатам В и L воспользуемся формулами, выведенными для референц-эллипсоида Красовского:
| x = | 6367558,4969(Bрад) − {ao − | [0,5 + (a4 + a6l2 )l 2 ]l2 N}sinB cosB ; | (2.9) |
| y(L) = [1+ (a3 + | a5l 2 )l 2 ]lN cosB . | (2.10) | |
| В формулах (2.9) и (2.10) приняты следующие обозначения: | |||
| l = ( L | — Lo )² / ρ² — разность долгот определяемой точки | и осевого | |
| меридиана зоны в радианной мере; |
r² = 206264,8062² — число секунд в одном радиане;
Bрад = B² / r² — широта точки, выраженная в радианной мере;
N = 6399698,902 — [21562,267 – (108,973 – 0,612 cos2B) cos2B] cos2B; N – один из главных радиусов кривизны референц-эллипсоида Красовского (радиус кривизны первого вертикала);
ао = 32140,404 — [135,3302 – (0,7092 – 0,0040 cos2B) cos2B ] cos2B; а3 = (0,3333333 + 0,001123 cos2B) cos2B – 0,1666667;
а4 = (0,25 + 0,00252 cos2B ) cos2B – 0,04166;
а5 = 0,0083 — [0,1667 — (0,1968 + 0,0040 cos2B) cos2B] cos2B; а6 = (0,166 cos2B – 0,084) cos2B.
При высокоточных геодезических работах значения широт и долгот вычисляют до 0,0001² , а значения координат х и у(L) — до 0,001 м.
По формуле (2.10) значение координаты у(L) получают относительно осевого меридиана зоны, т.е. оно может получиться со знаками «плюс» (для восточной части зоны) или «минус» (для западной части зоны). Для записи координаты у в зональной системе координат необходимо вычислить рассто-
31
яние до точки от осевого меридиана зоны, отнесенного на запад на 500 км, а впереди полученного значения приписать номер зоны. Например, получено значение у(L) = — 303678,774 м в 47 зоне. Тогда
у = 47 (500000,000 – 303678,774) = 47196321,226 м.
Пример вычисления плоских прямоугольных координат по геодезическим координатам приведен в табл. 2.3.
Зная прямоугольные координаты точек, можно вычислить геодезические координаты (обратный расчет). Такие вычисления выполняют для контроля вычисления координат. Т.е. при решении любых задач на перевычисление координат обратный расчет позволяет оценить правильность получаемых величин.
Формулы для вычисления геодезических координат по прямоугольным координатам имеют следующий вид:
| В = Вх — [1 — ( b4 – 0,12 z2) z2 ] z2 b2 r² ; | (2.11) |
| L = Lo + l ; | (2.12) |
| l = [ 1 – ( b3 — b5 z2) z2] z r² . | (2.13) |
В формулах (2.11) и (2.12):
Nx² = b² + {50221746 + [293622 + (2350 + 22cos2b)cos2b]cos2b}10-10sinbcosb r² ;
b² = [( х /6367558б4969)] r² ; z = у(L) / ( Nx сos Bx );
Nx = 6399698,902 — [21562,267 – (108,973 – 0,612 cos2Bx) cos2Bx] cos2Bx; b2 = (0,5 + 0,003369 cos2Bx ) sin Bx cos Bx ;
b3 = 0,333333 – ( 0,166667 – 0,001123 cos2Bx ) cos2 Bx ; b4 = 0,25 + (0,16161 + 0,00562 сos2Bx) cos2 Bx ;
b5 = 0,2 – (0,1667 – 0,0088 сos2Bx) cos2Bx .
Предварительно по значению у определяют номер зоны, в которой расположена определяемая точка, по номеру зоны определяют долготу Lo осевого меридиана и по расстоянию от точки до отнесенного на запад осевого меридиана находят расстояние у(L) от точки до осевого меридиана зоны (последнее может быть со знаком плюс или минус). Пример вычисления геодезических координат по прямоугольным приведен в табл. 2.3.
Преобразование прямоугольных координат Гаусса из зоны в зону предусматривает выполнение вычислений по тем и другим формулам.
Предположим, что в зоне 12 (на ее краю в восточной части) имеется точка А с прямоугольными координатами хА и уА. Необходимо найти ее координаты в зоне 13.
Алгоритм решения задачи следующий.
1.По формулам (2.11), (2.12) и (2.13) вычисляют геодезические координаты точки А ВА и LА (прямой расчет).
2.По полученным геодезическим координатам ВА и LА по формулам (2.9)
и(2.10) вычисляют прямоугольные координаты точки А в зоне 12 (обратный расчет) и убеждаются в совпадении их значений с исходными координатами.
Пример 2.5. Точка имеет геодезические координаты: широту В = 47о02’15,0543″ и долготу L = 65о01’38,2456″. Вычислить прямоугольные координаты точки с обратным расчетом .
32
| Таблица 2.3 | ||||
| №№ | Вычисление х и у | Вычисление B и L | ||
| п/п | Параметр | по В и L | Параметр | по x и y |
| 1 | B° | 47о02’15,0543″ | β рад | 0,818760380 |
| 2 | B» | 169335,0543″ | β» | 168881,4511″ |
| 3 | B»/ρ» | 0,820959510 | β° | 46о54’41,4512″ |
| 4 | Sin B | 0,731800091 | Sin β | 0,730299573 |
| 5 | Cos B | 0,681519352 | Cos β | 0,683127026 |
| 6 | Cos2 B | 0,464468627 | Cos2 β | 0,466662533 |
| 7 | lo | +2о01’38,2456″ | B х рад | 0,821272741 |
| 8 | l»/ ρ» | +0,035382893 | B х« | 169399,6627″ |
| 9 | N | 6389707,353 м | B х° | 47о03’19,6628″ |
| 10 | ао | 32077,69996 | Sin B х | 0,732013528 |
| 11 | а4 | 0,075000799 | Cos B х | 0,681290096 |
| 12 | а6 | -0,003204001 | Cos2 Bх | 0,464156195 |
| 13 | а3 | -0,011601574 | Nx | 6389714,058 м |
| 14 | а5 | -0,026270237 | Nx Cos B х | 4353248,903 м |
| 15 | l2 | 0,001251949 | z | +0,035394247 |
| 16 | N l2 | 7999,587730 м | z2 | 0,001252753 |
| 17 | Х | 5213504,617 м | B | 47о02’15,0542″ |
| 18 | y(L) | +154079,966 м | lо | +2о01’38,2456″ |
| 19 | y | 11654079,966 м | L | 65о01’38,2456″ |
Примечания:
1. Во второй части таблицы не приведены значения коэффициентов b.
2.Расхождения в значениях B, равное 0,0001″ можно считать допустимым, поскольку погрешность в определении координаты x в этом случае составляет немногим более 3 мм (1″ дуги меридиана примерно соответствует 33 м).
3.Используя полученные геодезические координаты ВА и LА, с учетом значения долготы осевого меридиана зоны 13, т.е. зоны, в которую производится перевычисление координат, по формулам (2.9) и (2.10) определяют прямоугольные координаты точки А в зоне 13 (прямой расчет).
4.Обратным расчетом, используя полученные координаты точки А в зоне 13, по формулам (2.11), (2.12) и (2.13), убеждаются в правильности вычислений, т.е. в совпадении значений геодезических координат, полученных в п.1.
Если нет необходимости в точном вычислении координат точек, например, для углов съемочных трапеций, при предварительной оценке прямоугольных координат точек местности при использовании геологических карт мелких масштабов и др., то пользуются упрощенными формулами, либо специальными таблицами.
33
Книга найдена на
http://www.geolink-group.com/tourclub/ — спасибо создателям
Вы можете заказать 2CD
с картами Юга России
Содержание книги
1.10.
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ НА КАРТАХ
Прямоугольные координаты
(плоские) — линейные величины: абсцисса Х и ордината
Y,
определяющие положение точек на плоскости (на карте) относительно двух
взаимно перпендикулярных осей Х и
Y
(рис. 14). Абсцисса Х и ордината
Y
точки А—расстояния от начала координат до оснований перпендикуляров,
опущенных из точки А на соответствующие оси, с указанием знака.
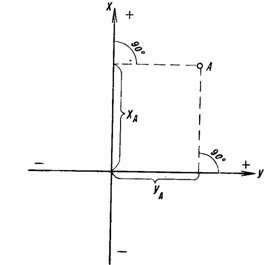
Рис. 14.
Прямоугольные координаты
В топографии и геодезии, а также на
топографических картах ориентирование производится по северу со счетом углов
по ходу часовой стрелки, поэтому для сохранения знаков тригонометрических
функций положение осей координат, принятое в математике, повернуто на 90°.
Прямоугольные координаты на
топографических картах СССР
применяются по координатным зонам. Координатные зоны — части земной
поверхности, ограниченные меридианами с долготой, кратной 6°. Первая зона
ограничена меридианами 0° и 6°, вторая—б» и 12°, третья—12° и 18° и т.д.
Счет зон идет от Гринвичского меридиана
с запада на восток. Территория СССР располагается в 29 зонах: от 4-й до 32-й
включительно. Протяженность каждой зоны с севера на юг порядка 20000 км.
Ширина зоны на экваторе около 670 км, на широте 40°— 510 км, т
широте 50°—430 км, на широте 60°—340 км.
Все топографические карты в пределах
данной зоны имеют общую систему прямоугольных координат. Началом координат в
каждой зоне служит точка пересечения среднего (осевого) меридиана зоны с
экватором (рис. 15), средний меридиан зоны соответствует
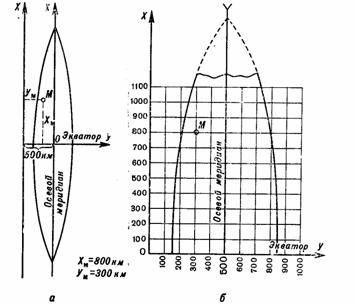
Рис. 15.
Система прямоугольных координат на топографических картах: а—одной зоны;
б—части зоны
оси абсцисс, а экватор — оси ординат.
При таком расположении координатных осей абсциссы точек, расположенных южнее
экватора, и ординаты точек, расположенных западнее среднего меридиана, будут
иметь отрицательные значения. Для удобства пользования координатами на
топографических картах принят условный счет ординат, исключающий
отрицательные значения ординат. Это достигнуто тем, что отсчет ординат идет
не от нуля, а от величины 500 км, Т. е. начало координат в каждой
зоне как бы перенесено на 500 км влево вдоль оси
Y.
Кроме того, для однозначного определения положение точки по прямоугольным
координатам на земном шаре к значению координаты
Y
слева приписывается номер зоны (однозначное или двузначное число).
Зависимость между условными
координатами и их действительными значениями выражается формулами:
X‘
= Х-, У =
У— 500 000,
где
X‘
и Y‘—действительные
значения ординат;
X,
Y
— условные значения ординат.
Например, если точка имеет координаты
Х =
5 650 450:
Y
= 3 620
840,
то это значит, что точка расположена в
третьей зоне на удалении 120 км 840 м от среднего меридиана
зоны (620840—500000) и к северу от экватора на удалении 5650 км 450
м.
Полные координаты
— прямоугольные координаты, записанные (названные) полностью, без каких-либо
сокращений. В примере, приведенном выше, даны полные координаты объекта:
Х
= 5 650 450;
Y
= 3620
840.
Сокращенные координаты
применяются для ускорения целеука-зания по топографической карте, в этом
случае указываются только десятки и единицы километров и метры. Например,
сокращенные координаты данного объекта будут:
Х = 50
450;
Y
= 20 840.
Сокращенные координаты нельзя применять
при целеуказании на стыке координатных зон и если район действий охватывает
пространство протяженностью более 100 км по широте или долготе.
Координатная (километровая) сетка—сетка
квадратов на топографических картах, образованная горизонтальными и
вертикальными линиями, проведенными параллельно осям прямоугольных координат
через определенные интервалы (табл.
5).
Эти линии называются километровыми. Координатная сетка предназначается для
определения координат объектов и нанесения на карту объек тов по их
координатам, для целеуказания, ориентирования карты, измерения дирекционных
углов и для приближенного определения расстояний и площадей.
Таблица 5 Координатные сетки на картах
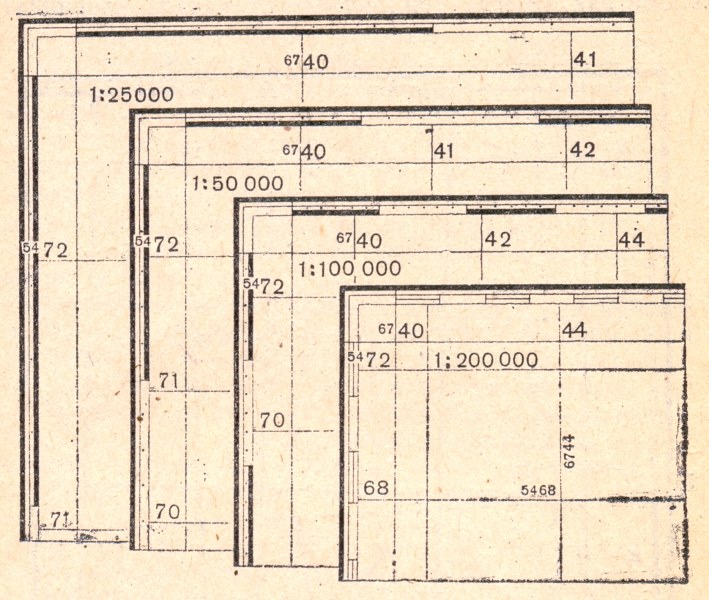
| Масштабы карт | Размеры сторон квадратов | Площади квадратов, кв. | |
| на карте, см | на местности, км | ||
| 1:25 000 | 4 |
| |
| 1:50 000 | 2 | 1 | 1 |
| 1:100 000 | 2 | 2 | 4 |
| 1:200 000 | 2 | 4 | 16 |
На карте масштаба 1:500 000
координатная сетка полностью не показывается; наносятся только выходы
километровых линий по сторонам рамки (через 2 см). При необходимости
по этим выходам координатная сетка может быть прочерчена на карте.
Километровые линии на картах
подписываются у их зарамочных выходов и у нескольких пересечений внутри
листа (рис. 16). Крайние на листе карты километровые линии подписываются
полностью, остальные—сокращенно, двумя цифрами (т. е. указываются только
десятки и единицы километров). Подписи у горизонтальных линий соответствуют
расстояниям от оси ординат (экватора) в километрах. Например, подпись 6082 в
правом верхнем углу показывает, что данная линия отстоит от экватора на
удалении 6082 км.
Подписи вертикальных линий обозначают
номер зоны (одна или две первых цифры) и расстояние в километрах (всегда три
цифры) от начала координат, условно перенесенного к западу от среднего
меридиана на 500 км. Например, подпись 4308 в левом нижнем углу
означает: 4 — номер зоны, 308 — расстояние от условного начала координат в
километрах.
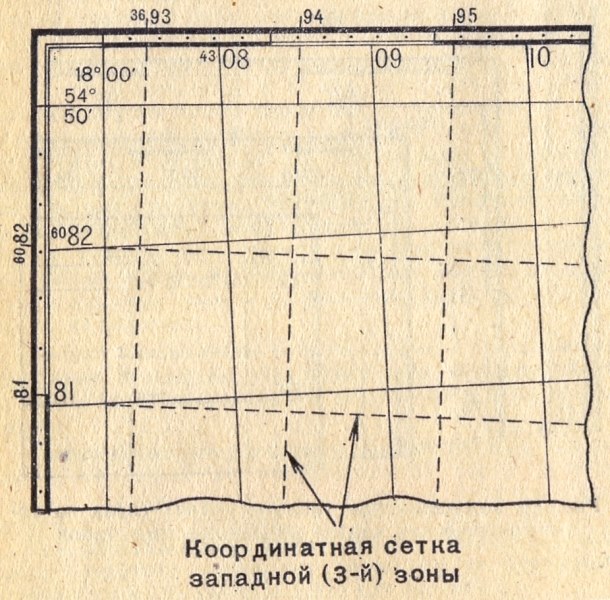
Дополнительная координатная
(километровая) сетка может быть нанесена на топографических картах масштаба
1:25 000, 1:50000, 1:100000 и 1:200000 по выходам километровых линий в
смежной западной или восточной зоне. Выходы километровых линий в виде
черточек с соответствующими подписями даются на картах, расположенных на
протяжении 2° к востоку и западу от граничных меридианов зоны.
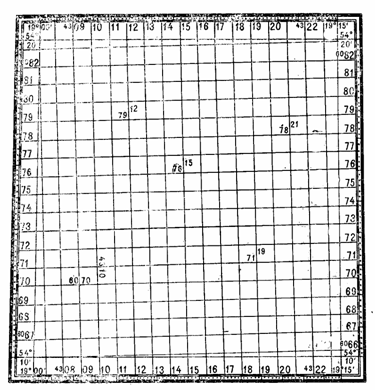
рис.
16.
Координатная (километровая) сетка на листе карты
Дополнительная координатная сетка
предназначается для преобразования координат одной зоны в систему координат
другой, соседней, зоны.
На рис. 17 черточки на внешней стороне
западной рамки с подписями 81,6082 и на северной стороне рамки с подписями
3693, 94, 95 и т.д. обозначают выходы километровых линий в системе координат
смежной (третьей) зоны. При необходимости дополнительная координатная сетка
прочерчивается на листе карты путем соединения одноименных черточек на
противоположных сторонах рамки. Вновь построенная сетка является
продолжением километровой сетки листа карты смежной зоны и должна полностью
совпадать (смыкаться) с ней при склейке карты.
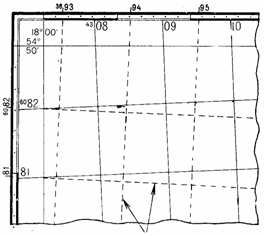
Координатная сетка
западной (3-й) зоны
Рис. 17. Дополнительная координатная
сетка
Вы
можете заказать 2CD с картами Юга России
Комментарии:
Сообщение от: Денчик
Спасибо за материал)
Сообщение от: Bitte
Таможенный импортер «ВЭД ЛАЙН», предлагающий. Действуя на внешнеторговом рынке грузоперевозок, мы настроили действенную цепочку поставок, позволяющую своим клиентам осуществлять перевозку «от двери до двери». Мы не только доставляем ваш груз на оптово розничные рынки России или любую точку России, наша компания обеспечивает простое таможенное оформление и подготавливают необходимый пакет документов. В индивидуальном запросе наши специалисты предложат самый эффективный вид транспорта и организуют маршрут с минимальными датами и тарифом перевозки. За каждой отгрузкою из Китая мы организовываем оптимальный маршрут что спасает наших покупателей и сроки в пути и деньги. Поручить поставку из КНР вы можете связавшись с нашей компанией. Вам необходимо будет сообщить параметры вашего товара: его вес, размер, объем и тип. Вы сообщаете точный адрес доставки в Российской Федерации. Мы оказываем самый эффективный способ комбинированной перевозки морским, железнодорожным или авто транспортом и строим короткий фрахт. На случай если вам нужна дешевая поставка, вам следует выбрать сквозной сервис.
Прямоугольные координаты
(плоские) — линейные величины (абсцисса X и ордината У), определяющие положение точки на плоскости (карте) относительно двух
взаимно перпендикулярных осей X и У. Абсцисса X и ордината У точки А — расстояния от начала
координат до оснований перпендикуляров, опущенных из точки А на соответствующие оси, с указанием знака.
В топографии и геодезии ориентирование производится по северу со счетом углов по ходу часовой стрелки. Поэтому для сохранения знаков тригонометрических
функций положение осей координат, принятое в математике, повернуто на 90° (за ось X принята вертикальная линия, за ось У —
горизонтальная).
Прямоугольные координаты (Гаусса) на топографических картах
применяются по координатным зонам, на которые делится поверхность Земли при изображении ее на картах в проекции Гаусса. Координатные зоны — части земной
поверхности, ограниченные меридианами с долготой, кратной 6°. Счет зон идет от Гринвичского меридиана с запада на восток. Первая зона ограничена
меридианами 0 и 6°, вторая — 6° и 12°, третья —12° и 18° и т.д. (например, территория СССР располагалась в 29 зонах: от 4-й до 32-й включительно).
Протяженность каждой зоны с севера на юг составляет примерно 20 000 км. Ширина зоны на экваторе равна примерно 670 км, на широте 40° — 510 км, на широте
50° — 430 км, на широте 60° — 340 км.
Все топографические карты в пределах одной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения
среднего (осевого) меридиана зоны с экватором (рис.2.1), средний меридиан зоны соответствует оси абсцисс (X), а экватор — оси
ординат (Y).
Рис. 2.1 Система прямоугольных координат на топографических картах:
а – одной зоны;
б – части зоны
При таком расположении координатных осей абсциссы точек, расположенных южнее экватора, и ординаты точек, расположенных западнее среднего меридиана, будут
иметь отрицательные значения. Для удобства пользования координатами на топографических картах принят условный счет ординат, исключающий отрицательные
значения координаты У. Это вызвано тем, что отсчет ординат идет не от нуля, а от величины 500 км, т.е. начало координат в каждой зоне как бы
перенесено на 500 км влево вдоль оси У.
Кроме того, для однозначного определения положения точки по прямоугольным координатам на земном шаре к значению координаты у слева приписывается
номер зоны (однозначное или двузначное число). Если, например, точка имеет координаты х = 5 650 450; у = 3 620 840, то это значит, что
она расположена в третьей зоне на удалении 120 км 840 м (620 840 — 500 000) к востоку от среднего меридиана зоны и на удалении 5 650 км 450 м к
северу от экватора.
Полные координаты
— прямоугольные координаты, указанные полностью, без каких-либо сокращений. В примере, приведенном выше, даны полные координаты точки.
Сокращенные координаты
применяются для ускорения целеуказания по топографической карте. В этом случае указывают только десятки и единицы километров и метры, например, х = 50 450; у = 20 840. Сокращенные координаты нельзя применять, если район действий охватывает пространство протяженностью более 100 км
по широте или долготе.
Координатная (километровая) сетка
(рис.2.2) — сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных
координат через определенные интервалы: на карте масштаба 1:25000 — через 4 см, на картах масштабов 1:50000, 1:100000 и 1:200000 — через 2 см. Эти линии
называются километровыми.
Рис. 2.2 Координатная (километровая) сетка на топографических картах различных масштабов
На карте масштаба 1:500000 координатная сетка полностью не показывается, наносятся только выходы километровых линий по сторонам рамки (через 2 см). При
необходимости по этим выходам координатная сетка может быть прочерчена на карте.
Координатная сетка используется для определения прямоугольных координат и нанесения на карту точек, объектов, целей по их координатам, для целеуказания и
отыскания на карте различных объектов (пунктов), для ориентирования карты на местности, измерения дирекционных углов, приближенного определения расстояний
и площадей.
Километровые линии на картах подписываются у их выходов за рамкой листа и в девяти местах внутри листа карты. Ближайшие к углам рамки километровые линии,
а также ближайшее к северо-западному углу пересечение линий подписываются полностью, остальные сокращенно, двумя цифрами (указываются только десятки и
единицы километров). Подписи у горизонтальных линий соответствуют расстояниям от оси ординат (от экватора) в километрах. Например, подпись 6082 в правом
верхнем углу (рис.2.3) показывает, что данная линия отстоит от экватора на удалении 6 082 км.
Подписи у вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно
перенесенного к западу от среднего меридиана на 500 км. Например, подпись 4308 в левом верхнем углу означает: 4 — номер зоны, 308 — расстояние от условного
начала координат в километрах.
Рис. 2.3 Дополнительная координатная сетка
Дополнительная координатная (километровая) сетка
предназначается для преобразования координат одной зоны в систему координат другой, соседней зоны. Она может быть нанесена на топографических картах
масштабов 1:25000, 1:50000, 1:100000 и 1:200000 по выходам километровых линий в смежной западной или восточной зоне. Выходы километровых линий в виде
черточек с соответствующими подписями даются на картах, расположенных на протяжении 2° к востоку и западу от граничных меридианов зоны.
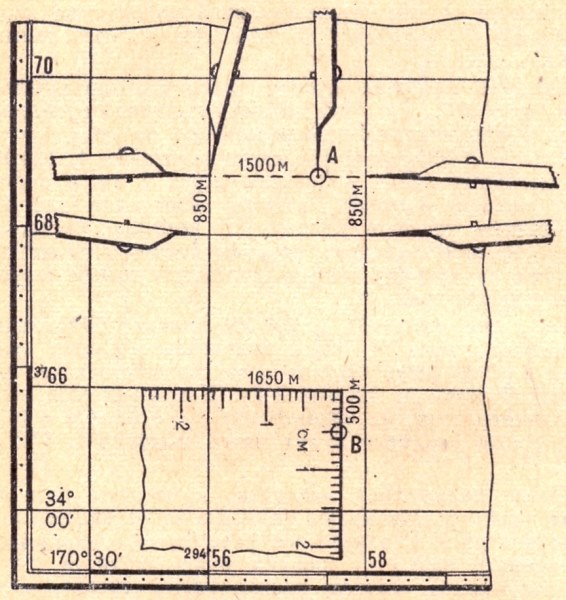
На рис.2.3 черточки на внешней стороне западной рамки с подписями 81 6082 и на северной стороне рамки с подписями 3693 94 95 обозначают выходы километровых
линий в системе координат смежной (третьей) зоны. При необходимости дополнительная координатная сетка прочерчивается на листе карты путем соединения
одноименных черточек на противоположных сторонах рамки. Вновь построенная сетка является продолжением километровой сетки листа карты смежной зоны и должна
полностью совпадать (смыкаться) с ней при склейке карты.
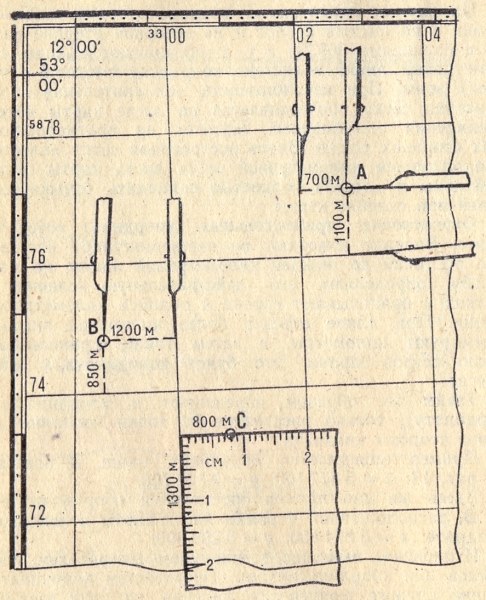
Определение прямоугольных координат точек по карте
. Вначале измеряют по перпендикуляру расстояние от точки до нижней километровой линии, по масштабу определяют его действительную величину в метрах и
приписывают справа к подписи километровой линии. При длине отрезка более километра вначале суммируют километры, а затем также приписывают число метров
справа. Это будет координата х (абсцисса). Таким же образом определяют и координату у (ординату), только расстояние от точки измеряют до
левой стороны квадрата.
Пример определения координат точки А показан на рис.2.4: х = 5 877 100; у = 3 302 700. Здесь же дан пример определения координат
точки В, расположенной у рамки листа карты в неполном квадрате: х = 5 874 850; у = 3 298 800.
Рис. 2.4 Определение прямоугольных координат точек по карте
Измерения выполняют циркулем-измерителем, линейкой или координатомером. Простейшим координатомером служит офицерская линейка, на двух взаимно
перпендикулярных краях которой имеются миллиметровые деления и надписи х и у.
При определении координат координатомер накладывают на квадрат, в котором располагается точка, и, совместив вертикальную шкалу с его левой стороной, а
горизонтальную — с точкой, как показано на рис.2.4, снимают отсчеты.
Отсчеты в миллиметрах (десятые миллиметра отсчитывают на глаз) в соответствии с масштабом карты преобразуют в действительные величины — километры и
метры, а затем величину, полученную по вертикальной шкале, суммируют (если она больше километра) с оцифровкой нижней стороны квадрата или приписывают к
ней справа (если величина меньше километра). Это будет координата х точки.
Таким же образом получают и координату у — величину, соответствующую отсчету по горизонтальной шкале, только суммирование производят с оцифровкой
левой стороны квадрата.
На рис.2.4 показан пример определения прямоугольных координат точки С: х = 5 873 300; у = 3 300 800.
Нанесение точек на карту по прямоугольным координатам. Прежде всего, по координатам в километрах и оцифровкам километровых линий находят на карте квадрат,
в котором должна быть расположена точка.
Квадрат местонахождения точки на карте масштаба 1:50000, где километровые линии проведены через 1 км, находят непосредственно по координатам объекта в
километрах. На карте масштаба 1:100000 километровые линии проведены через 2 км и подписаны четными числами, поэтому если одна или две координаты точки в.
километрах нечетные числа, то нужно находить квадрат, стороны которого подписаны числами на единицу меньше соответствующей координаты в километрах.
На карте масштаба 1:200000 километровые линии проведены через 4 км и подписаны числами, кратными 4. Они могут быть меньше соответствующей координаты
точки на 1, 2 или 3 км. Например, если даны координаты точки (в километрах) х = 6755 и у = 4613, то стороны квадрата будут иметь оцифровки 6752 и
4612.
После нахождения квадрата, в котором расположена точка, рассчитывают удаление ее от нижней стороны квадрата и полученное расстояние откладывают в
масштабе карты от нижних углов квадрата вверх. К полученным точкам прикладывают линейку и от левой стороны квадрата также в масштабе карты откладывают
расстояние, равное удалению объекта от этой стороны.
На рис.2.5 показан пример нанесения на карту точки А по координатам х = 3 768 850, у = 29 457 500.
Рис. 2.5 Нанесение точек на карту по прямоугольным координатам
При работе с координатомером вначале также находят квадрат, в котором расположена точка. На этот квадрат накладывают координатомер, совмещают его
вертикальную шкалу с западной стороной квадрата так, чтобы против нижней стороны квадрата был отсчет, соответствующий координате х. Затем, не
изменяя положения координатомера, находят на горизонтальной шкале отсчет, соответствующий координате у. Точка против отсчета покажет ее
местоположение, соответствующее данным координатам.
На рис.2.5 показан пример нанесения на карту точки В, расположенной в неполном квадрате, по координатам х = 3 765 500; у = 29 457 650.
В данном случае координатомер наложен так, что горизонтальная шкала его совмещена с северной стороной квадрата, а отсчет против западной его стороны
соответствует разности координаты у точки и оцифровки этой стороны (29 457 км 650 м — 29 456 км = 1 км 650 м). Отсчет, соответствующий разности
оцифровки северной стороны квадрата и координаты х (3766 км — 3765км 500 м), отложен по вертикальной шкале вниз. Местоположение точки В
будет против штриха у отсчета 500 м.
Напомним, что географические координаты (широта и долгота) – это угловые величины, определяющие
положение объектов на земной поверхности и на карте. При этом широта точки — это угол, составленный плоскостью экватора и нормалью к поверхности земного
эллипсоида, проходящей через данную точку. Счет широт ведется по дуге меридиана от экватора к полюсам от 0 до 90°; в северном полушарии широты называют
северными (положительными), в южном — южными (отрицательными).
Долгота точки — это двугранный угол между плоскостью Гринвичского меридиана и плоскостью меридиана данной точки. Счет долготы ведется по дуге экватора
или параллели в обе стороны от начального меридиана, от 0 до 180°. Долготу точек, расположенных к востоку от Гринвича до 180°, называют восточной
(положительной), к западу — западной (отрицательной).
Географическая (картографическая, градусная) сетка
— изображение на карте линий параллелей и меридианов; используется для определения географических (геодезических) координат точек (объектов) и
целеуказания. На топографических картах линии параллелей и меридианов являются внутренними рамками листов; их широта и долгота подписываются на углах
каждого листа. Географическая сетка полностью показывается лишь на топографических картах масштаба 1:500000 (параллели проведены через 30′, а меридианы —
через 20′) и 1:1000000 (параллели проведены через 1°, а меридианы — через 40′). Внутри каждого листа карты на линиях параллелей и меридианов подписаны их
широта и долгота, которые позволяют определять географические координаты на большой склейке карт.
На картах масштабов 1:25000, 1:50000, 1:100000 и 1:200000 стороны рамок разделены на отрезки, равные в градусной мере 1′. Минутные отрезки оттенены через
один и разделены точками (за исключением карты масштаба 1:200000) на части по 10″. Кроме того, внутри каждого листа карт масштабов 1:50000 и 1:100000
показывается пересечение средних параллели и меридиана и дается их оцифровка в градусах и минутах, а вдоль внутренней рамки даны выходы минутных делений
штрихами длиной 2—3 мм, по которым можно прочертить параллели и меридианы на карте, склеенной из нескольких листов.
Если территория, на которую создана карта, находится в западном полушарии, то в северо-западном углу рамки листа правее подписи долготы меридиана
помещается надпись «К западу от Гринвича».
Определение географических координат точки по карте производится по ближайшим к ней параллели и меридиану, широта и долгота которых известны. Для этого на
картах, масштабов 1:25000 — 1:200000 следует предварительно провести южнее точки параллель и западнее — меридиан, соединив линиями соответствующие штрихи
по сторонам рамки листа (рис.2.6). Затем от проведенных линий берут отрезки до определяемой точки (Аа1 Аа2), прикладывают
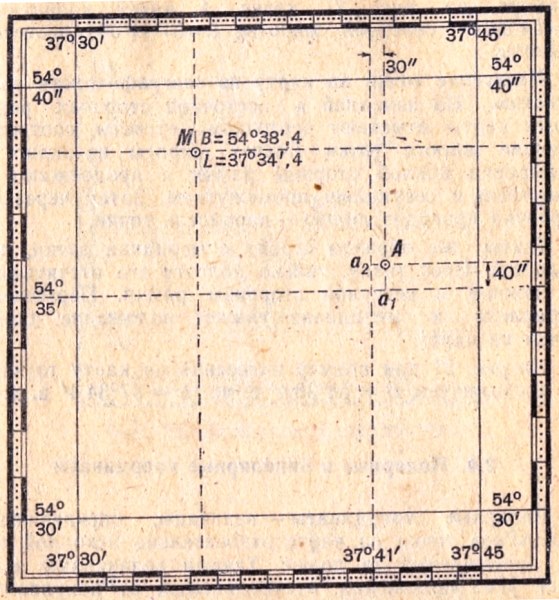
их к градусным шкалам на сторонах рамки и производят отсчеты. В примере на рис.1.2.6 точка А имеет координаты В = 54°35’40» северной широты, L = 37°41’30» восточной долготы.
Нанесение точки на карту по географическим координатам
. На западной и восточной сторонах рамки листа карты отмечают черточками отсчеты, соответствующие широте точки. Отсчет широты начинают от оцифровки южной
стороны рамки и продолжают по минутным и секундным промежуткам. Затем через эти черточки проводят линию — параллель точки.
Таким же образом строят и меридиан точки, проходящий через точку, только долготу его отсчитывают по южной и северной сторонам рамки. Пересечение параллели
и меридиана укажет положение данной точки на карте. На рис.2.6 дан пример нанесения на карту точки М по координатам В = 54°38,4′ с.ш., L = 37°34,4′ в.д.
Рис. 2.6 Определение географических координат по карте и нанесение точек на карту по географическим координатам
Как было указано выше, в силу особенностей формы, внутреннего строения и движения в пространстве земной эллипсоид имеет истинные (географические) и
магнитные полюса, не совпадающие друг с другом.
Северный и Южный географические полюсы — это точки, через которые проходит ось вращения земного шара, а Северный и Южный магнитные полюсы – это полюсы
гигантского магнита, которым, собственно, является Земля, причем Северный магнитный полюс (≈ 74°с.ш., 100°з.д.) и Южный магнитный полюс (≈ 69°ю.ш.,
144°в.д.) постепенно дрейфуют и, соответственно, не имеют постоянных координат. В этой связи важно понимать, что магнитная стрелка компаса указывает именно
на магнитный, а не на истинный (географический) полюс.
Таким образом, существуют истинный и магнитный полюсы, не совпадающие между собой, соответственно этому существуют истинный (географический) и магнитный меридианы. И от того и от другого можно отсчитывать направление
на нужный объект: в одном случае наблюдатель будет иметь дело с истинным азимутом, в другом — с магнитным.
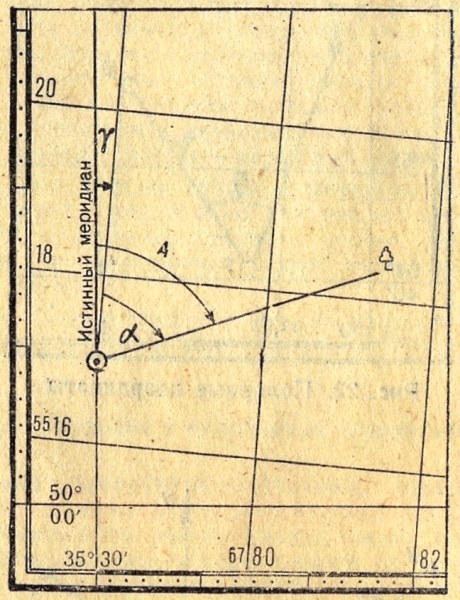
Рис. 2.7 Истинный азимут А, дирекционный угол α, и сближение меридианов γ
Истинный азимут
— это угол А (рис.2.7), измеряемый по ходу часовой стрелки от 0 до 360° между северным направлением истинного (географического)
меридиана и направлением на определяемый пункт.
Магнитный азимут
— это угол Ам, измеряемый по ходу часовой стрелки от 0 до 360° между заданным (выбранным) направлением и направлением
на Север на местности.
Обратный азимут
— азимут (истинный, магнитный) направления, противоположного определяемому (прямому). Он отличается от прямого на 180°, и его можно отсчитать по компасу
против указателя у прорези.
Понятно, что истинный и магнитный азимуты отличаются, как минимум, на ту же самую величину, на которую магнитный меридиан отличается от истинного. Эта
величина называется магнитным склонением. Другими словами, магнитное склонение – угол δ ( дельта) между истинным и магнитным меридианами.
На величину магнитного склонения оказывают влияние различные магнитные аномалии (залежи руд, подземные потоки и т.д.), суточные, годовые и вековые
колебания, а также временные возмущения под действием магнитных бурь. Величина магнитного склонения и его годовые изменения указаны на каждом листе
топографической карты. Суточное колебание магнитного склонения достигает 0,3° и при точных измерениях магнитного азимута учитывается по графику поправок,
составленному в зависимости от времени суток. На картах масштабов 1:500000 и 1:1000000 показываются районы магнитных аномалий, и в каждом из них
подписывается значение амплитуды колебания магнитного склонения. Если стрелка компаса отклоняется от истинного меридиана к востоку, магнитное склонение
называют восточным (положительным), если стрелка отклоняется к западу, склонение называют западным (отрицательным). Соответственно, восточное склонение
часто обозначают знаком «+», западное — знаком «—».
Дирекционный угол
— это угол α (альфа), измеряемый на карте по ходу часовой стрелки от 0 до 360° между северным направлением вертикальной
линии координатной сетки и направлением на определяемый пункт. Другими словами, дирекционный угол — это угол между заданным (выбранным) направлением и
направлением на Север на карте (рис.2.7). Дирекционные углы измеряются по карте, а также определяются по измеренным на местности
магнитным или истинным азимутам.
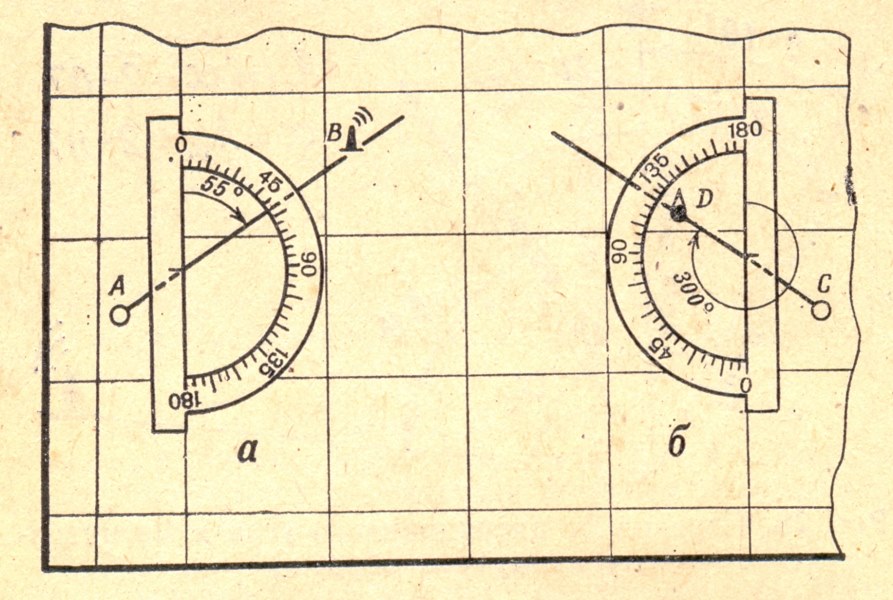
Рис. 2.8 Измерение дирекционного угла транспортиром
Измерение и построение дирекционных углов на карте производится с помощью транспортира (рис.2.8).
Чтобы измерить на карте дирекционный угол какого-нибудь направления, надо наложить на нее транспортир так, чтобы середина его линейки, отмеченная
штрихом, совпала с точкой пересечения определяемого направления с вертикальной километровой линией сетки, а край линейки (т.е. деления 0 и 180° на
транспортире) совместился с этой линией. Затем следует отсчитать по шкале транспортира угол по ходу часовой стрелки от северного направления километровой
линии до определяемого направления.
Для построения на карте в какой-либо точке дирекционного угла проводят через эту точку прямую, параллельную вертикальным линиям километровой сетки,
и от этой прямой строят заданный дирекционный угол.
Следует учитывать, что средняя ошибка измерения угла транспортиром, имеющимся на офицерской линейке, составляет 0,5°.
Значения истинного азимута и дирекционного угла отличаются друг от друга на величину сближения меридианов. Сближение меридианов —
угол ? (гамма) между северным направлением истинного меридиана данной точки и вертикальной линией координатной сетки
(рис.2.7). Сближение меридианов отсчитывается от северного направления истинного меридиана до северного направления вертикальной линии сетки. Для точек,
расположенных восточнее среднего меридиана зоны, величина сближения положительная, а для точек, расположенных западнее, — отрицательная. Величина
сближения меридианов на осевом меридиане зоны равна нулю и возрастает с удалением от среднего меридиана зоны и от экватора, при этом ее максимальное
значение не превышает 3°.
Сближение меридианов, указываемое на топографических картах, относится к средней (центральной) точке листа; величина ее в пределах листа карты масштаба
1:100000 на средних широтах у западной или восточной рамки может отличаться на 10-15′ от значения, подписанного на карте.
Переход от дирекционного угла к магнитному азимуту и обратно
может производиться различными способами: по формуле, с учетом годового изменения магнитного склонения, по графической схеме. Удобен переход через поправку
направления. Необходимые данные для этого имеются на каждом листе карты масштабов 1:25000—1:200000 в специальной текстовой справке и графической схеме,
помещаемых на полях листа в левом нижнем углу (рис.2.9).
Рис. 2.9 Данные о величине поправки направления
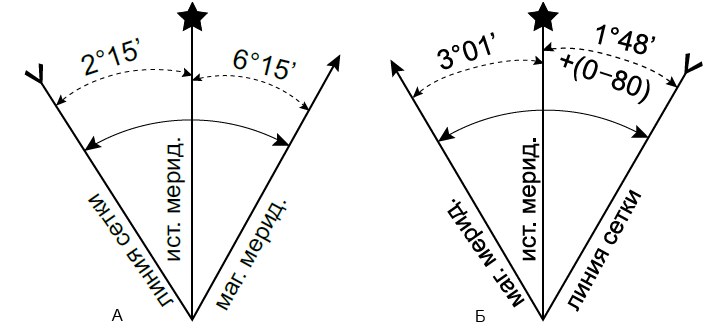
При этом в специальной текстовой справке ключевой фразой является: «Поправка в дирекционный угол при переходе к магнитному азимуту плюс (минус)…»,
также важен угол между «стрелочкой» и «вилочкой»:
- если «вилочка» слева, а «стрелочка» справа (рис.2.10-А), то склонение восточное и при переходе от дирекционного угла к азимуту
поправка (2°15′ + 6°15′ = 8°30′) от величины измеренного дирекционного угла отнимается (соответственно, при
переходе от азимута к дирекционному углу, поправка прибавляется); - если «вилочка» справа, а «стрелочка» слева (рис.2.10-Б), то склонение западное и при переходе от дирекционного угла к азимуту
поправка (3°01′ + 1°48′ = 4°49′) к величине измеренного дирекционного угла прибавляется (соответственно, при
переходе от азимута к дирекционному углу, поправка отнимается).
Рис. 2.10 Внесение поправки
Внимание!
Невнесение поправки в дирекционный угол или магнитный азимут, особенно при больших расстояниях и крупных масштабах карт, ведет к значительным ошибкам в
определении координат, промежуточных и конечных точек маршрута.
Местоположение интересующих нас точек на карте обычно определяют с помощью координат.
При определении координат точек местности по карте применяют географические, плоские прямоугольные и полярные координаты.
Географические координаты (рис. 21) представляют собой угловые величины (широту и долготу), которые определяют положение точки на земной поверхности относительно экватора и меридиана, принятого за начальный.

Географическая широта — это угол, образованный плоскостью экватора и отвесной линией в данной точке земной поверхности. В зависимости от расположения точки относительно экватора географическая широта может быть северной или южной. Очевидно, что широта точки, расположенной на экваторе, равна 0°, а на полюсах — 90°.
Географическая долгота — это угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку.
Для единообразия в определении долготы точек за начальный меридиан принято считать Гринвичский меридиан. В зависимости от расположения точки относительно начального меридиана до меридиана 180° она имеет восточную или западную долготу.
Линии, соединяющие одинаковые по широте точки земной поверхности, называют параллелями. Линии, соединяющие одинаковые по долготе точки земной поверхности, называют меридианами. Меридианы и параллели являются рамками листов топографических карт.
Географические координаты на карте определяют по рамкам листа (рис. 22), подписанным в углах, и залитым штрихам (минутным делениям).
Например, на нашем рисунке западная рамка листа карты (меридиан) имеет долготу 14° 00′, южная рамка (параллель) имеет широту 54°15′.
Географические координаты даются через одну минуту на рамках карт масштабом от 1:10 000 до 1 : 200 000 и через 5 минут на рамках карт масштабом 1 : 500 000 и 1 : 1 000 000.

1 Меридиан, проходящий через астрономическую обсерваторию Е Гринвиче (около Лондона).
2 С 1960 г. на рамках карт масштабов от 1 : 25 000 до 1 : 100 000 минутное деление дополнительно разбито на шесть равных частей по 10″.
Для определения географических координат точки на карте (например, точки Б на рис. 22) необходимо провести меридиан и параллель через концы ближайших к точке одноминутных делений рамки.
В нашем примере проведенный меридиан имеет долготу 14° 01′, а проведенная параллель имеет широту 54° 16′. Затем оценивают на глаз или измеряют доли минуты по долготе и широте до интересующей нас точки и добавляют их к основным отсчетам.
В результате широта точки Б равна 54° 16′, 3, долгота — 14° 01’, 4.
Географическими координатами обычно пользуются при определении положения точек, удаленных одна от другой на значительные расстояния.
Под плоскими прямоугольными координатами понимают линейные величины, характеризующие относительное положение точки на плоскости. Поясним сущность их на рис. 23.

Пусть на плоскости проведены две взаимно перпендикулярные линии, одна из которых проходит в вертикальном, а вторая (У) в горизонтальном направлении. Назовем эти линии осями координат, а точку их пересечения О — началом координат.
Тогда положение любой точки на плоскости в данной системе координат относительно начала координат будет определяться кратчайшими расстояниями до нее от осей координат. Эти расстояния в виде прямых линий, перпендикулярных к одной из координатных осей и параллельных другой, являются координатами точек (х и у). Ось Х-ов принято также называть осью абцисс, а ось У-ов — осыо ординат.
Из рис. 23 видно, что в зависимости от положения точки по отношению к осям координат ее абсцисса и ордината могут иметь положительные и отрицательные значения.
Поскольку земную поверхность, имеющую шарообразную форму, нельзя изобразить па плоскости без разрыва и искажений, ее условно разделили на 60 равных частей, ограниченных меридианами через 6° по долготе.
’ Счет их ведут от Гринвичского меридиана, который является западным для первой зоны.
Эти части называют координатными зонами, для каждой из которых в любом масштабе изготовляют свои отдельные карты, состоящие из многих листов.
В каждой такой зоне осями координат являются: осью ординат, то есть осью У-ов — экватор, осыо абцисс, то есть осью Х-ов — осевой меридиан зоны.
Пересечение осевого меридиана с экватором принято за начало координат. Таким образом, каждая зона имеет свои собственные оси и начало координат, то есть свою отдельную систему координат.
Эта система называется системой плоских прямоугольных координат.
Система плоских прямоугольных координат в каждой зоне имеет вполне определенное географическое положение, поэтому она непосредственно связана с системой географических координат и с системами прямоугольных координат всех остальных зон.
Для простоты определения координат на плоскость (карту) наносят сетку квадратов, линии которой параллельны осям координат. Такую сетку принято называть координатной сеткой.
Если на каждую координатную зону отдельно нанести координатную сетку со сторонами квадратов в масштабе карты, то такая сетка будет являться графическим выражением плоской прямоугольной системы координат.
Счет координат х ведется от экватора к полюсам. Значения координат х к северу от экватора положительные, а к югу — отрицательные.
Счет координат у ведется от осевого меридиана. Значения координат у к востоку осевого меридиана имеют знак плюс, к западу — знак минус.
Очевидно, что для территории СССР, расположенной в северном полушарии, значения всех координат х будут положительными, а значения координат у могут быть как положительными, так и отрицательными, в зависимости от расположения точки по отношению к осевому меридиану зоны.
Для удобства пользования координатами, чтобы иметь только один положительный знак, ордината точки пересечения осевого меридиана зоны и экватора в СССР принята равной 500 км, а не нулю. В связи с этим все координаты у, идущие на восток от осевого меридиана, будут больше 500 км, а идущие на запад — меньше 500 км.
На листах топографических карт, как отмечалось выше, нанесена километровая или координатная сетка. Около каждой линии записаны их координаты (рис. 22). Так, надпись 6015 означает, что все точки, расположенные на горизонтальной линии (линии У-ов), находятся от экватора на расстоянии 6015 км.
Надпись 3435 у вертикальной линии (линии Х-ов) показывает: 3 — номер зоны, а 435 — ординату линии в километрах, расположенную на западе от осевого меридиана зоны на 65 км (500 км — 435 км = 65 км).
Если бы данная вертикальная линия обозначалась трехзначной цифрой больше 500, то это означало бы, что линия находится на востоке от осевого меридиана.
Последующие линии километровой сетки обозначены лишь двузначными числами, чтобы не было повторений.
Найдем в прямоугольных координатах положение точки, обозначенной на карте отметкой 151,8. Для этого надо измерить по перпендикулярам расстояние от этой Отметки до горизонтальной и вертикальной линий и полученные значения сложить с координатами линий.
Расстояния можно измерять с помощью измерителя или линейки, а также с помощью координатной мерки или координатомера.
При определении координат точки используется координатная мерка или координатомер того масштаба карты, по которой определяется местоположение этой точки.
![]()
![]()
Для определения координат точек по карте лучше всего пользоваться измерителем и поперечным масштабом.
Для определения положения точек, кроме прямоугольных координат, широко применяют так называемые полярные координаты, особенно при ориентировании и целеуказании. Сущность полярных координат заключается в том, что положение точки характеризуется углом от какого-то направления, принятого за начальное, и дальностью от исходной точки до определяемой.
Вертикальные линии километровой сетки, как известно, в каждой координатной зоне параллельны своему осевому меридиану. Поэтому при склейке смежных листов двух соседних зон их километровые линии, располагаясь под углом одна к другой, не совпадают.
Как же быть в этом случае при определении координат точек карты с помощью километровой сетки?
На всех листах карт, располагающихся на к востоку от западной границы каждой зоны, сделаны метки (между внешней и минутной рамками), которые обозначают продолжение линий координатной сетки соседней западной зоны. Эти метки оцифрованы в соответствии с нумерацией километровых линий соседней зоны. Оцифровка помещается за внешней рамкой листа.
Когда приходится использовать листы карты на стыке двух зон, а требуется работать в единой системе координат, прежде всего необходимо решить (если это не указано старшим начальником), какую координатную зону следует применять.
В соответствии с этим на том листе карты, на котором имеются штрихи километровой сетки соседней зоны, нужно соединить эти штрихи друг с другом остро отточенным карандашом, построив таким образом километровую сетку западной зоны. В последующем на этом листе карты при определении координат точек пользуются лишь прочерченной координатной сеткой.
А когда район работ с картой переместится от стыка зон, переходят к работе в той зоне, в которой предстоит действовать дальше.
Связанные статьи:
1. Что такое местность?
2. Назначение и содержание топографических карт
3. Классификация топографических карт
4. Подготовка карты к работе
5. Измерительные приемы, применяемые при работе с картой
6.
Топографическое ориентирование по карте
7. Изучение местности по карте
8. Оценка маршрута движения, выбранного или назначенного по карте
9. Определение координат точек по карте
10. Целеуказание по карте
11. Топографическая привязка с помощью карты
12.
Хранение и сбережение карт
Решение задач по топографической карте. Определение номенклатуры листа карты. Определение координат точек на карте. Определение углов ориентирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
ПО КУРСУ «ГЕОДЕЗИЯ ч.1»
6. РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКОЙ КАРТЕ
6.I. ОПРЕДЕЛЕНИЕ НОМЕНКЛАТУРЫ ЛИСТА КАРТЫ
При решении ряда проектных и изыскательских задач возникает необходимость в поиске нужного листа карты заданного масштаба для определенного участка местности, т.е. в определении номенклатуры данного листа карты.
Определить номенклатуру листа карты можно по географическим координатам точек местности на данном участке.
При этом можно также использовать плоские прямоугольные координаты точек, так как имеются формулы и специальные таблицы для пересчета их в соответствующие географические координаты.
- ПРИМЕР.Определить номенклатуру листа карты масштаба 1: 10 000 по географическим координатам точки М:
- широта = 52048’37’’; долгота L = 100°I8′ 4I».
- Сначала необходимо определить номенклатуру листа карты масштаба
I: I 000 000, на котором расположена точка М c заданными координатами. Как известно, земная поверхность делится параллели-ми, проводимыми через 4°, на ряды, обозначаемые заглавными буквами латинского алфавита. Точка N c широтой 52°48’37 » находится в I4-м ряду от экватора, расположенном между параллелями 52о и 56°.
Этому ряду соответствует I4-я буква латинского алфавиты -N. Известно также, что земная поверхность делится меридианами, проводимыми через 6°, на 60 колонн. Колонны нумеруются арабскими цифра-ми с запада на восток, начиная c меридиана c долготой I80°.
Номера колонн отличаются от номеров соответствующих им 6-градусных зон проекции Гаyсса на 30 единиц. Точка М c долготой 100°18′ 4I» находится в 17-й зоне, расположенной между меридианами 96° и 102°. Этой зоне соответствует колонна c номером 47.
Номенклатура листа карты масштаба I: 1 000 000 слагается из буквы, обозначающей данный ряд, и номера колонны. Следовательно, номенклатура листа карты масштаба 1: 1 000 000, на котором расположена точка М, будетN-47.
Далее необходимо определить номенклатуру листа карты масштабы I: 100 000, на который попадает точкаM. Листы карты масштаба 1: 100 000 получают делением листа нарты масштаба 1: I 000 000 на 144 части (рис. 8).
Разобьем каждую сторону листаN-47 на 12 равных частой и соединим соответствующие точки отрезками параллелей и меридианов.Полученные листы карты масштаба 1: 100 000 нумеруются арабскими цифрами и имеют размеры: 20 ‘ — по широте и 30’- по долготе. Из рис.
8 видно, что точка M с заданными координатами попадает на лист карты масштаба I: 100 000 e номером 117. Номенклатура данного листа будет N-47-117.
Листы карты масштаба I: 50 000 получают делением листа карты масштабаI: 100 000 на 4 части и обозначают заглавными буквами русского алфавита (рис. 9). Номенклатура листа этой карты, на который попадает точна М,будет N- 47- 117.
B свою очередь, листы карты масштаба I: 25 000 получают делением листа карты масштаба I: 50 000 на 4 части и обозначают строчными буквами русского алфавита (рис. 9).
Точка M с заданными координатами попадает на лист карты масштаба I: 25 000, имеющий номенклатуру N-47-117 –Г-А.
Наконец, листы карты масштаба 1: 10 000 получают делением листа карты масштаба 1: 25 000 на 4 части и обозначают арабскими цифрами. Из рис. 9 видно, что точка М располагается на листе карты этого масштаба, имеющем номенклатуруN-47-117-Г-А-1.
Ответ к решению данной задачи помещают на чертеже.
6.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ ТОЧЕК НА КАРТЕ
Для каждой токи на топографической карте можно определить ее географические координаты (широту и долготу) и прямоугольные координаты Гаусса х, у.
Для определения этих координат используется градусная и километровая сетки карты. для определения географических координат точки Р проводят ближайшие к данной точке южную параллель и западный меридиан, соединив одноимённые минутные деления градусной рамки (рис. 10).
Определяют широту Во и долготу Lо точки Ао пересечения проведенных меридиана и параллели. Через заданную точку Р проводя тлинии, параллельные проведенным меридиану и параллели, и измеряют при помощи миллиметровой линейки расстояния В= А1Р и L= А2P, а также размеры минутных делений широты С и долготы на карты. Географические координаты точки Р определяют по формулам Cl
- — широта: Bp=Bo+*60’’
- — долгота: Lp=Lo+*60’’, измеряют до десятых долей миллиметра.
- Расстояния b,l,Cb,Cl измеряют до десятых долей миллиметра.
Для определения прямоугольных координат точки Р используют километровую сетку карты. С помощью оцифровки этой сетки на карте находят координаты Х ои Уо юго-западного угла квадрата сетки, в котором находится точка Р (рис. 11).
Затем из точки Р опускают перпендикуляры С1Л и C2Л на стороны этого квадрата. С точностью до десятых долей миллиметра измеряют длины этих перпендикуляров ∆Х и ∆У и с учетом масштаба карты определяют их фактические значения на местности.
Например, измеренное расстояние С1Р равно 12,8 мы, a масштаб карты 1: 10 000. Согласно масштабу, I мм на карте соответствует 10 м не местности, а значит,
- ∆Х= 12,8 х 10 м = 128 м.
- После определения значений ∆Х и ∆У находят прямоугольные координаты точки Р по формулам
- Xp=Xo+∆X
- Yp=Yo+∆Y
- Точность определения прямоугольных координат точки зависит от масштаба карты и может быть найдена по формуле
- t=0.1*M, мм,
- где М-знаменатель масштаба карты.

- Например, для карты масштаба I: 25 000 точность определения координат Х и У составляет t= 0,1 х 25 000 = 2500 мм = 2,5 м.
6.3. ОПРЕДЕЛЕНИЕ УГЛОВ ОРИЕНТИРОВАНИЯ ЛИНИЙ
К углам ориентирования линий относятся дирекционный угол, истинный и магнитный азимуты.
Для определения по карте истинного азимута некоторой линии ВС (рис.12) используют градусную рамку карты. Через начальную точку В этой линии проводят параллельно вертикальной линии градусной рамки лини истинного меридиана (пунктирная линияNS), а затем геодезическим транспортиром измеряют величину истинного азимута Авс.
Для определения пo карте дирекционного угла некоторой линии ДЕ (рис. I2) используют километровую сетку карты. Через начальную точку D проводят параллельно вертикальной линии километровой сетки (пунктирная линия KL). Проведенная линия будет параллельной оси абсцисс проекции Гаусса, т.
е, осевому меридиану данной зоны. Дирекционный угол αdeизмеряют геодезическим транспортом относительно проведенной линии KL.
Следует отметить, что и дирекционный угол и истинный азимуты отсчитываются,а следовательно, и измеряются по часовой стрелке относительно начального направления до ориентируемой линии.
Кроме непосредственного измерения дирекционного угла линии на карте с помощью транспортира, можно определить значение этого угла другим способом. Для этого определения прямоугольные координаты начальной и конечной точек линии (Хд,Уд,Хе,Уе). Дирекционный угол данной лини может быть найден по формуле
- При выполнении вычислений по данной формуле с помощью микрокалькулятора следует помнить, что уголt=arctg(∆y/∆x) является не дирекционном, а табличным углом. Значение дирекционного угла в этом случае необходимо определить с учетом знаков ∆Х и ∆У по известным формулам приведения:
-

- -угол α лежит в І четверти:∆Х>0; ∆Y>0; α=t;
- -угол α лежит во IIчетверти:∆Х0; α=180o-t;
- -угол α лежит в IIIчетверти:∆Х
Как определить прямоугольные координаты на топографической карте
Координаты являются методом обозначения точки на карте. В картографии используются различные координаты: плоские, прямоугольные, угловые, биполярные и полярные. В целях обозначения объектов недвижимого имущества на топографических картах применяются прямоугольные координаты. Ведь определение прямоугольных координат на топографических картах гораздо проще и точнее.
Понятие прямоугольных координат

Прямоугольные координаты представлены в виде точек пересечения предполагаемых линий по данным взаимно перпендикулярных осей на плоской поверхности. Обычно данные оси на плоскости условно обозначаются латинскими буквами x (абсцисса), y (ордината). Предполагаемые линии, пересечение которых является точкой местоположения, определяются по целым и дробным числовым показателям на указанных осях.
В классической науке такая система носит название декартовая система. Однако классическая система Декарта и применяемая в целях топографического обозначения объектов на карте несколько различаются между собой. Так, в системе расположение осей повернуто на 90 градусов по углу. Названа такая система в честь основателя – Гаусса.
Система Гаусса используется для разделения всей территории Земли на отдельные зоны. Внутри каждой из зон координат идёт обозначение своих числовых выражений предполагаемых линий определения точек. Важным моментом является установление точки отсчёта внутри зоны.
Обычно в качестве такой точки выступает место пересечения срединного меридиана в полосе с экватором планеты. Данная точка не имеет материальной величины, так что обозначается она в качестве нулевой отметки, а её значение всегда равно нулю.
В целом такая система имеет вид сетки с бесконечным количеством числовых значений. Там могут отображаться две группы числовых значений:
- Значения со знаком минус – для обозначения объектов, находящихся южнее и к западу нулевой отметки.
- Положительные числовые значения – для указания мест расположения точек восточнее и севернее центральной точки системы координат.
Однако это не полная характеристика значений, указываемых в прямоугольных координатах точек на топографических картах. К примеру, при обозначении точек расположения на топографических картах отрицательные значение не используются.
Координатные зоны по системе Гаусса по всей земной поверхности пронумерованы. При обозначении точек на отдельных зонах помимо координат внутри самой зоны указывается номер, который приурочен к указанному квадрату по системе Гаусса.
Данный номер указывается перед отрицательными значениями координат на оси ординат. На оси абсцисс номер зоны не указывается. Указание номера означает смещение нулевой отметки на 500 км в левую сторону. Это сделано, чтобы исключить наличие значений со знаком минус на карте.
Значения обозначаются в километрах и равны они промежутку от нулевой отметки на оси до соответствующего места на карте.
Значение при этом указывается двояко:
- Полные координаты – указывается промежуток с точностью до метра.
- Сокращённые координаты – обозначаются лишь километры до десятков и метры.
Однако в основном используются полные координаты, так как точное указание местоположения точки имеет большое значение в топографических целях. Сокращённые координаты допускается использовать лишь в случае, когда топографическая карта охватывает не более 10 тысяч квадратных километров, т. е. реальные длины осей не превышают ста километров.
При обозначении отрицательного значения на оси У указывается сначала ось, потом номер зоны по системе Гаусса и в конце промежуток от нулевой отметки до объекта на карте. Примерно, прямоугольные координаты точки на топографической карте выглядят следующим образом: х = 5 650 450; у = 3 620 840.
В подобном случае значение по оси Х толкуется прямо, а для установления отдалённости точки по ординате от нулевой отметки из указанного значения вычитается 500 километров. А это значит, что точка в указанном примере находится в 5 650 километрах и 450 метрах от экватора и 120 километрах и 840 метрах от срединного меридиана.
Определение точек на карте по координатной сетке
Координатную сеть иначе ещё называют километровой, так как на мелких картах величина квадратов сетки равняется километру. На подобных картах километровая сеть изображается в виде линий, прочерченных параллельно осями и имеющих определённый интервал между собой. Интервал устанавливается в зависимости от масштаба.
Так, при масштабе 1 : 25 000 значение интервала равняется 4 сантиметрам. При большем масштабе интервал не бывает меньше 2 сантиметров, невзирая на реальное расстояние между линиями. При масштабе больше чем 1 : 500 000 сетка прямо не изображается. Обозначаются лишь выходные метки по краям карты.
Координатная сеть является условной для отдельной зоны, и для сопоставления топографии соседних зон по краям карты оставляются отметки сетки, которые соответствуют выходам сетки соседней зоны.
При обозначении значений координат на топографических картах координатная сеть позволяет быстрее обозначить необходимую точку. Отсчет расстояния идёт от границ квадрата координатной сетки. Каждая из сторон отдельного квадрата сетки имеет заранее определенную реальную длину в километрах (1, 2 и т. д. километров).
Чтобы осуществить определение координат точек на картах, очень важно иметь ориентиры. Если изначальное координаты ясны и нужно лишь указать их на карте, то делается это следующим образом:
- Определяется квадрат на сетке по километру координат.
- При помощи линейки отсчитываются метровые величины внутри квадрата, сначала по параллельной линии к оси абсцисс, затем к оси ординат.
- Вдоль линий указываются метровые значения.
В целом процедура завершена. Однако на практике не всё так просто. Зачастую не имеется значения изначальных координат. В таких случаях важно иметь определенные ориентиры, без которых найти точку представляется невозможным. В качестве ориентира может послужить любая близлежащая точка с известными координатами. Достаточно выяснить реальное расстояние между известной точкой и искомым объектом.
Указать адрес точки на карте на 100 % точно невозможно, так что определяются примерные значения.
С другой стороны, современные технологии позволяют произвести точные измерения на месте с моментальным отображением результатов на электронной топографической карте. Для этого применяются методы лазерного измерения или радиолокации. В любом случае при практической необходимости выяснения местоположения того или иного объекта недвижимости правильным решением будет обратиться к специалистам.
В качестве специалистов могут выступать:
- инженеры государственной службы геодезии и картографии (кадастр);
- специалисты частных инженерных служб.
При этом частные инженерные службы в своём распоряжении имеют более высокотехнологичное, а значит и более точное оборудование, нежели государственные органы. Разумеется, услуги таких специалистов стоят не дёшево.
Соотношение прямоугольных координат с другими системами обозначения точек на карте
Помимо непосредственного использования прямоугольной системы или системы Гаусса часто возникает необходимость сопоставления данных в указанной системе и на обычной географической карте. В таких случаях используется несколько методов:
- Метод перевода значения из числового значения в стандартные значения (широты и долготы).
- Способ наложения значения расстояний по масштабу.
- Метод сопоставления географической карты с целой зоны Гаусса.
Практическое применение находит лишь первый метод, так как он признан официальным способом переложения координат объектов недвижимости из обычной топографической карты в географическую. Именно данный способ используют государственные службы и частные специалисты.
С другой стороны, это один из самых сложных способов, требующий специальных навыков и знаний. Кроме того необходимо наличие сведений о ключевых топографических точках.
Самым простым способом признаётся метод наложения расстояния. По сути, зная масштаб, вычислить координаты может даже школьник при помощи обычной линейки. Однако погрешность в таком случае может быть равна десяткам километров.
 Метод сопоставления карт применяется крайне редко. К примеру, такой способ может быть использован при корректировке генерального плана расширения населённых пунктов, определения границ регионов и государств.
Метод сопоставления карт применяется крайне редко. К примеру, такой способ может быть использован при корректировке генерального плана расширения населённых пунктов, определения границ регионов и государств.
Но данные методы позволяют не только решить частные проблемы, но и узнать координаты искомого объекта недвижимости. Такое стало возможным после предоставления открытого доступа к картам GPS. Постоянное спутниковое наблюдение за поверхностью земли позволило с точностью до метра определить местоположение практически любого объекта, не оснащенного радиопоглощающим покрытием.
Выяснить местоположение путем сопоставления данных с GPS и топографической карты может практически любой человек. Для этого необходимо:
- получить данные географических координат из системы GPS, выраженные в широте и долготе;
- по ним вычислить зону Гаусса (срединный меридиан в зоне);
- переложить точку соответственно зоне Гаусса.
Разумеется, задача не простая, но зато выполнимая. Другой вопрос – официальный статус такого вычисления.
Официальный статус определённых прямоугольных координат объектов недвижимости
Выявленные частным образом координаты никогда не будут иметь официального статуса. Ведь в целях топографии законодательством установлены специальные ГОСТы определения местоположения объектов недвижимости. Но при желании одним из вышеуказанных способов можно проверить соответствие официальных данных по тому или иному объекту недвижимости.
Очень редко, но всё же встречаются случаи, когда официальные данные в службе геодезистов не совсем точны. Никакого практического значения в повседневной жизни данный фактор может и не иметь. Однако он важен при определении так называемых «красных линий» на топографических картах. Это линии, по которым будут пролегать дороги и инженерные линии, и которые будут в будущем реквизированы.
Если по топографической карте данные объекта недвижимости указаны неверно, то его владелец может оказаться жертвой ошибочной реквизиции. Чтобы такого не случилось, при выявлении несоответствий фактических и официальных топографических координат необходимо сообщить об этом в уполномоченный орган (кадастр).
Если в удовлетворении ходатайства о проведении проверки и внесении изменений служба откажет, то можно добиться своего через суд. В таком случае будет назначена отдельная экспертиза с привлечением сторонних специалистов. В целом, процедура расходная и отнимает много времени, но рано или поздно владелец недвижимости может с таким столкнуться.
Плоские прямоугольные координаты, как определить плоские прямоугольные координаты по топографической карте
Линии параллелей и меридианов, которые служат рамкой для данного листа бумажнойтопографической карты, представляют собой кривые линии, хотя кривизна их в пределах одного листа практически и незаметна.
Но в пределах каждой зоны Гаусса имеются две линии, которые изображаются на карте прямыми линиями. Это осевой меридиан зоны и экватор.
Эти две линии приняты за оси плоских прямоугольных координат и определяют сами плоские прямоугольные координаты.
Линию осевого меридиана считают осью абсцисс и обозначают х, линию экватора — осью ординат и обозначают у. За начало координат принимают точку пересечения осевого меридиана с экватором. Таким ебразом, в каждой зонеГаусса имеется своя сетка плоских прямоугольных координат. Координаты х (абсциссы) отсчитываются к северу и югу от экватора, то есть от 0 (на экваторе) до 10 000 км (на полюсе).

К северу от экватора координата у считается положительной, к югу — отрицательной. Координаты ху (ординаты) отсчитываются от осевого меридиана вправо (к востоку) и влево (к западу). Чтобы не иметь дела с отрицательными значениями для этих координат, условились значение ординаты у для осевого меридиана принимать равным 500 км.
Тем самым ось х как бы переносится к западу на 500 км и все значения ординат в пределах данной зоны будут иметь всегда положительный знак. Кроме того, к значению ординаты у спереди всегда приписывается цифра, соответствующая номеру зоны Гаусса для того, чтобы избежать повторения координат, расположенных в разных зонах.
Как определить плоские прямоугольные координаты по топографической карте
Чтобы можно было определить плоские прямоугольные координаты точек в каждой зоне Гаусса на топографическихкартах наносится прямоугольная сетка координат, то есть проводятся линии, параллельные осевому меридиану и экватору.
Эти прямые линии, естественно, не будут совпадать с линиями, изображающими меридианы и параллели. За исключением осевого меридиана и экватора, параллельно которым они проводятся. Эту сетку координат называют километровой, так как ее линии проводятся через километр длямасштабов 1:10 000, 1:25 000, 1:50 000.

На каждом листе карты вдоль внутренней рамки даются значения координат километровой сетки от осевого меридиана данной зоны и от экватора. Значения полных координат подписываются только у крайних (верхней и нижней) линии сетки координат. У всех же промежуточных линий подписываются сокращенные обозначения, то есть только последние две цифры (десятки и единицы километров).
Например, нижняя линия километровой сетки на рисунке имеет обозначение 5042, а следующая над ней линия сетки обозначена только цифрой 43 км, а не 5043. Цифры километровой сетки под южной и над северной рамкой листа карты обозначают ординаты (у) этих линий. Крайние линии также обозначены полными координатами. Но в отличие от горизонтальных линий, первая цифра у ординат обозначает номер зоны.
Например, ордината у = 8384 км. Это значит, что лист данной карты расположен в восьмой шестиградусной зоне Гаусса, то есть ограниченной 42 и 48 меридианами восточной долготы, а точки, лежащие на линии у = 384, расположены слева от осевого меридиана на расстоянии 500-384=116 км.
С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любойточки на карте. С точностью до километра.
Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат.
Сначала обычно называется (записывается) значение координаты х — 5044, а затем у = 8384.
Указание какого-либо объекта на топографической карте с помощью плоских прямоугольных координат
Для указания какого-либообъекта на карте обычно говорят так: точка М находится в квадрате 50 448 384, то есть называют координаты ее подряд, не разделяя их, но чаще дают указания сокращенно, называют только две последующие цифры из плоских прямоугольных координат данной точки — квадрат 4484.
Называя этот квадрат на карте, мы указываем координаты левого нижнего его угла. То есть юго-западного угла квадрата, в котором расположена точка М.
Если необходимо указать более точное положение точки внутри этого квадрата, то дополнительно определяют ее расстояние от граничных линий этого квадрата.
Используя масштаб, переводят эти расстояния в метры и приписывают их к цифрам обозначенного квадрата.
Например, точка М имеет следующие координаты: х = 44 500 метров, а у = 84 500 метров. Это и будут сокращенные координаты для точки М, а полные плоские прямоугольные координаты для нее запишутся так: х = 5 044 500 м, у — 384 500 м.
Нанесение точек на карту по известным плоским прямоугольным координатам производится в обратной последовательности. Сначала отбрасываются три последние цифры в координатах и находятся линии километровой сетки. То есть квадрат, в котором расположена точка. Затем, с помощьюлинейки, масштаба и циркуля, наносятся точные координаты данной точки в этом квадрате.
Две сетки плоских прямоугольных координат на топографических картах
На некоторых топографических картах можно встретить две сетки плоских прямоугольных координат. Одна нанесена полностью так, как это было показано на рисунке выше.
Вторая обозначена только за рамкой данной карты.
В чем тут дело? Мы уже ранее установили, что вертикальные километровые линии параллельны осевому меридиану своей зоны, а осевые меридианы соседних зон между собой не параллельны.
Следовательно, при стыковке километровых сеток двух соседних зон линии одной из них располагаются под углом к линиям другой. Вследствие этого на стыке двух зон могут возникнуть затруднения вопределении координат, так как они будут относиться к разным осям координат.
Чтобы устранить это неудобство, в каждой шестиградусной зоне все листы карт, расположенные в пределах 2 градусов к востоку и 2 градусов к западу от границы зоны имеют помимо своей координатной сетки еще и дополнительную, являющуюся продолжением координатной сетки соседней зоны.
И для того чтобы не затемнять второй сеткой данные листы карты, ее обозначают лишь цифрами на внешней рамке листа. Цифры эти являются продолжением нумерации линий координатной сетки смежной зоны.
По материалам книги «Карта и компас мои друзья». Клименко А.И.
Как определить прямоугольные координаты точек на топографической карте?
Плоские прямоугольные координаты. При определении полных координат точки по оцифровке координатной линии, образующей южную сторону квадрата, в котором расположена точка, находят и записывают полное значение абсцисс х в километрах.
Как узнать прямоугольные координаты?
Прямоугольные координаты определяют с помощью координатной (километровой) сетки, представляющей собой сеть линий, параллельных экватору и осевому меридиану зоны.
Как определить географические и прямоугольные координаты точки на карте?
Прямоугольные координаты точки (х, у) по карте определяются с помощью километровой сетки. Абсциссы х, началом отсчета которых принимается линия экватора, подписаны у горизонтальных линий полностью только в углах рамки. В остальном указываются только две последние цифры, называемые сокращёнными координатами.
Что такое плоские прямоугольные координаты?
Прямоугольные координаты (плоские) — линейные величины: абсцисса Х и ордината Y, определяющие положение точек на плоскости (на карте) относительно двух взаимно перпендикулярных осей Х и Y (рис. 14).
Как на карте определить плоские прямоугольные координаты?
С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любой точки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат.
Как можно определить диаметр мяча?
Каковы размеры сетки квадратов прямоугольных координат на плане?
Сетку квадратов, в зависимости от масштаба плана, строят размерами 40 х 40 см или 50 х 50 см со стороной квадрата 10 см. … Контроль построения сетки квадратов выполняется проверкой диагоналей каждого квадрата одним раствором циркуля-измерителя, равным 141,4 мм. Разности диагоналей не должны быть более 0,2 мм.
Как определить широту и долготу на карте?
Важно: Географическая долгота измеряется от 0 до 180° . Чтобы определить географическую широту, нужно от заданной точки провести воображаемую прямую вдоль ближайшей параллели. Это и будет географическая широта. Она будет указана сбоку на карте.
Как определить географические координаты точки на карте?
Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна. Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом.
Какие координаты бывают?
Основные системы
- Декартовы координаты
- Полярные координаты
- Цилиндрические координаты
- Сферические координаты
- Декартовы и полярные
- Декартовы и цилиндрические
- Декартовы и сферические
- Цилиндрические и сферические
Как определить на карте координаты?
Как узнать координаты места