Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). Глава I Алгебраические дроби. Домашняя контрольная работа № 1 с ответами и решениями. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Домашняя контрольная работа № 1.
ДКР № 1 (транскрипт заданий)
1. При каких значениях переменной алгебраическая дробь (а — 8)/((а + 7)(а — 12)) равна нулю, а при каких не существует?
2. Сократите дробь (а^2 — ас + 2ab + b^2 — bс)/(ab — с^2 + ас + b^2)
3. Найдите значение выражения (а^2 — 4b^2 -5а + 10b)/((а + 2b)^2 — 25) при а = 1,9, b = 0,55.
4. Упростите выражение …
5. Упростите выражение …
6. Упростите выражение …
7. Найдите значение выражения … при x = — 3 3/4.
8. Упростите выражение …
9. Докажите, что значение выражения … не зависит от значений входящих в него переменных.
10. Решите задачу, выделяя три этапа математического моделирования.
Катер проходит 21 км по течению реки на 15 мин быстрее, чем то же расстояние против течения. Найдите собственную скорость катера, если скорость течения реки равна 1 км/ч.
ОТВЕТЫ на контрольную работу
Смотреть РЕШЕНИЯ заданий Варианта 1
Смотреть РЕШЕНИЯ заданий Варианта 2

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). Глава I Алгебраические дроби. Домашняя контрольная работа № 1 с ответами и решениями. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров: 16 824
ГДЗ(готовые домашние задания), решебник онлайн по алгебре за 7 класс автор Мордкович домашняя контрольная работа вариант 1 главы 1 — вариант решения домашней контрольной работы 1 главы 1
Глава 1. Домашняя контрольная работа:
1
2
Глава 2. Домашняя контрольная работа:
1
2
Глава 3. Домашняя контрольная работа:
1
2
Глава 4. Домашняя контрольная работа:
1
2
Глава 5. Домашняя контрольная работа:
1
2
Глава 6. Домашняя контрольная работа:
1
2
Глава 7. Домашняя контрольная работа:
1
2
Глава 8. Домашняя контрольная работа:
1
2
Глава 1. Математический язык. Математическая модель:
Глава 2. Линейная функция:
Глава 3. Системы двух линейных уравнений с двумя переменными:
Глава 4. Степень с натуральным показателем и ее свойства:
Глава 5. Одночлены. Арифметические операции над одночленами:
Глава 6. Многочлены. Арифметические операции над многочленами:
Глава 7. Разложение многочленов на множители:
Глава 8. Функция у = х^2:
Итоговое повторение:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). Домашняя контрольная работа № 1 с ответами и решениями (ГЛАВА 1. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ).
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Нажмите на этот спойлер, чтобы увидеть ЗАДАНИЯ
ДКР-1. Вариант 1
№ 1. Множество М состоит из всех двузначных чисел, которые при делении на 11 дают остаток 7. Задайте множество М, перечислив все его элементы.
Подсказка к решению: 18 : 11 = 1 (ост. 7), 29 : 11 = 2 (ост. 7), …
ОТВЕТ: М = (18; 29; 40; 51; 62; 73; 84; 95}.
№ 2. Приведите какое-нибудь словесное описание множества М = {1, 4, 9, 16, 25, …, 81}.
ОТВЕТ: Множество квадратов натуральных чисел, меньших 100.
№ 3. Для множеств А = [1; 5), В = [4; 6] и С = (–3; 2] найдите множество (А ∪ В) ∩ С.
Подсказка к решению: (A U B) = [1; 6] ∩ С = [1; 2].
ОТВЕТ: (A U B) ∩ С = [1; 2].
№ 4. Решите неравенство |2х + 4| ≤ 7.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
|2х + 4| ≤ 7 ⇒ –7 ≤ 2х + 4 ≤ 7
–11 ≤ 2х ≤ 3
–5,5 ≤ х ≤ 1,5.
№ 5. Найдите область определения выражения √[5x2 + 2х – 3].
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ

№ 6. Решите неравенство (x2 + 2,5x – 18)/(1,5x – 6) > 1.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
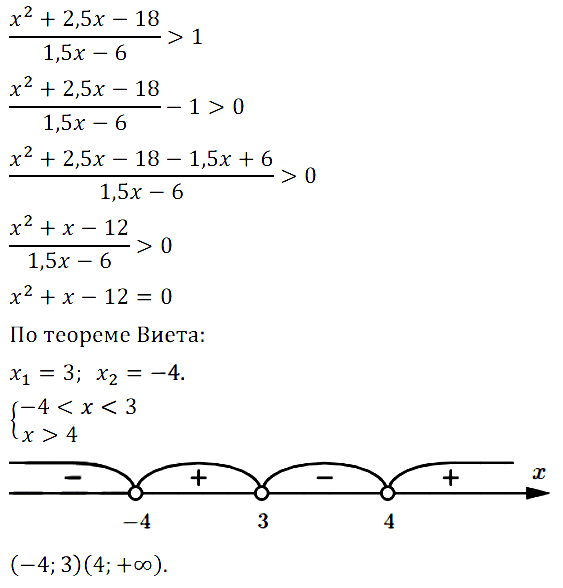
№ 7. Дано выражение у = f(х), где f(x) = ((3х – 1)2(2х + 3)(5 – х))/(х(х – 1)). Найдите значения переменной, при которых f(x) ≥ 0.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
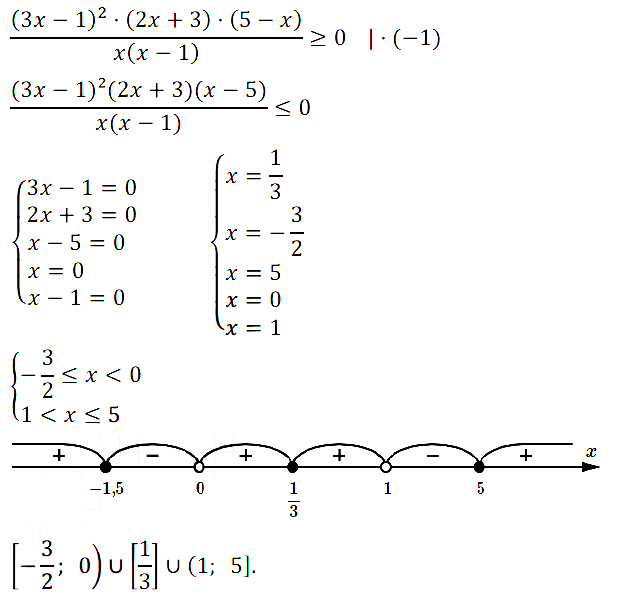
№ 8. Решите систему неравенств
{ 2x2 + 5х – 7 > 0; (3х – 4)/(2x + 6) ≤ 1.
Нажмите на этот спойлер, чтобы увидеть ЗАДАНИЯ
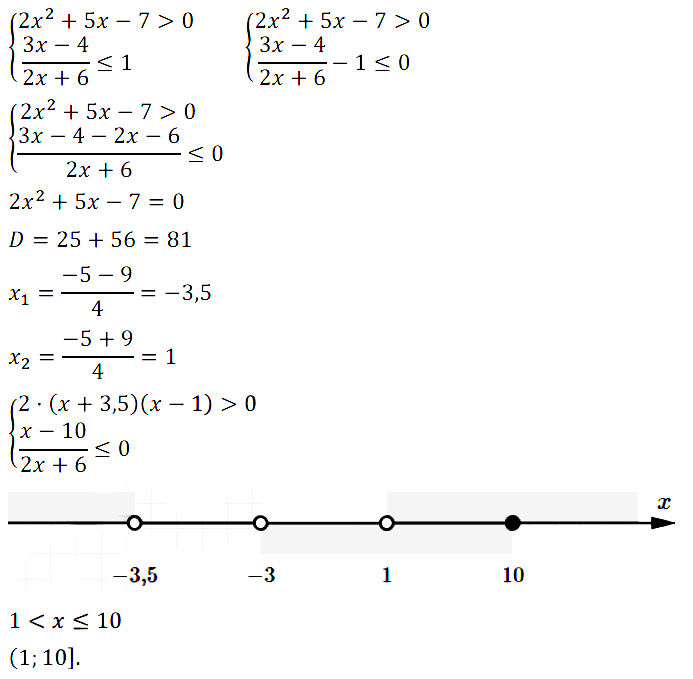
№ 9. Найдите длину отрезка, служащего решением двойного неравенства
–3 ≤ (5 + 3x)/4 ≤ –1. Укажите середину отрезка.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
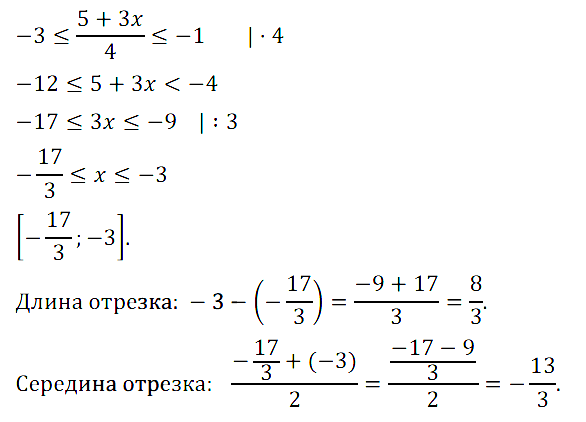
№ 10. Найдите все целые числа, удовлетворяющие системе неравенств
{ (2х – 11)/4 + (19 – 2x)/2 < 2x;
{ (2х + 15)/9 > (x – 1)/5 + x/3.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
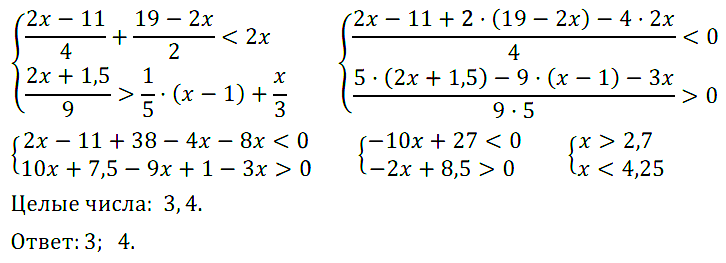
ДКР-1. Вариант 2
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ

№ 1. Множество М состоит из всех двузначных чисел, которые можно записать в виде n2 + 10, где n — натуральное число. Задайте множество М, перечислив все его элементы.
Подсказка к решению: 12 + 10 = 11, 22 + 10 = 14, …
ОТВЕТ: М = {11; 14; 19; 26; 35; 46; 59; 74; 91}.
№ 2. Приведите какое–нибудь словесное описание множества М = {10, 19, 28, 37, 46, …, 91}.
ОТВЕТ: Множество двузначных чисел, больше либо равных 10, с шагом плюс 9.
№ 3. Для множеств А = [1; 4), В = [2; 5] и С = (3; 7] найдите множество (А ∪ В) ∩ С.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
А = [1; 4); В = [2; 5]; С = (3; 7].
{А ∩ В) U С = [2; 4) ∩ С = [2; 7].
№ 4. Решите неравенство |4 – 3х| ≥ 6.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
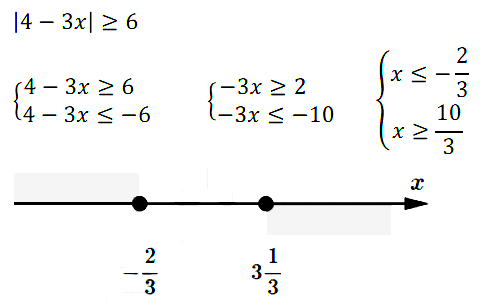
№ 5. Найдите область определения выражения √[8х – 15x2 – 1].
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
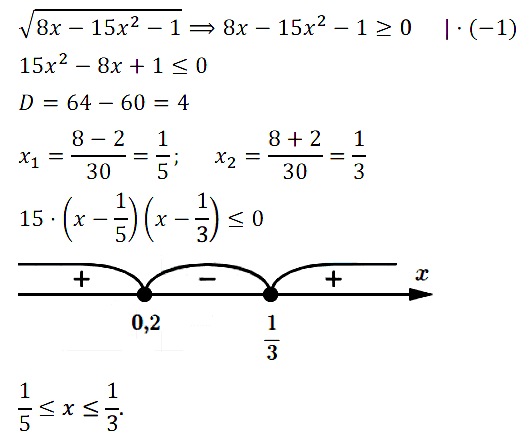
№ 6. Решите неравенство (x2 – 4,5х – 3)/(5 – 2,5х) ≤ 1.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
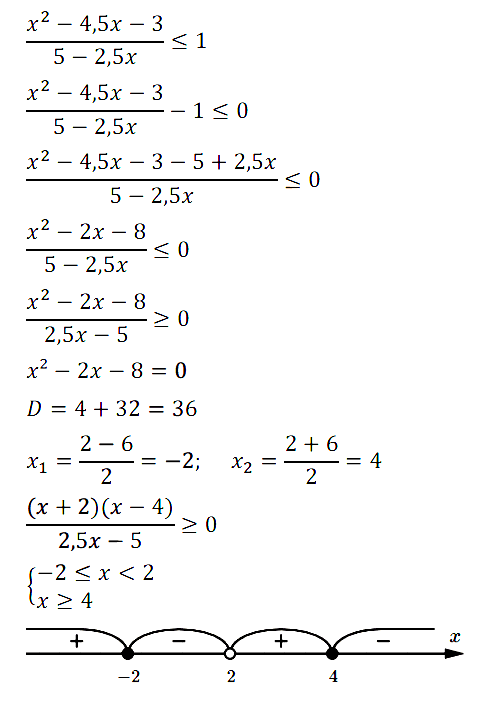
№ 7. Дано выражение у = f(x), где f(x) = ((2х – 3)2(3x + 1)(x – 3))/(x(2 – х)). Найдите значения переменной, при которых f(x) ≤ 0.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
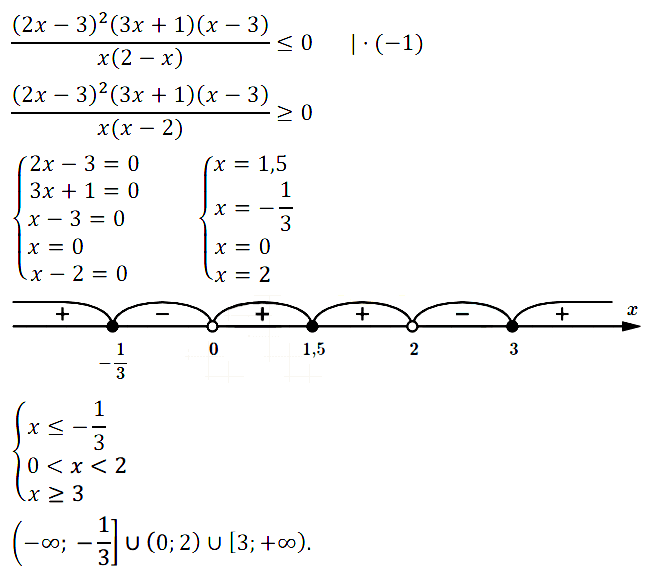
№ 8. Решите систему неравенств
{ 3x2 – 7х – 10 ≤ 0,
{ (2х – 1)/(2 – 3х) > 3.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
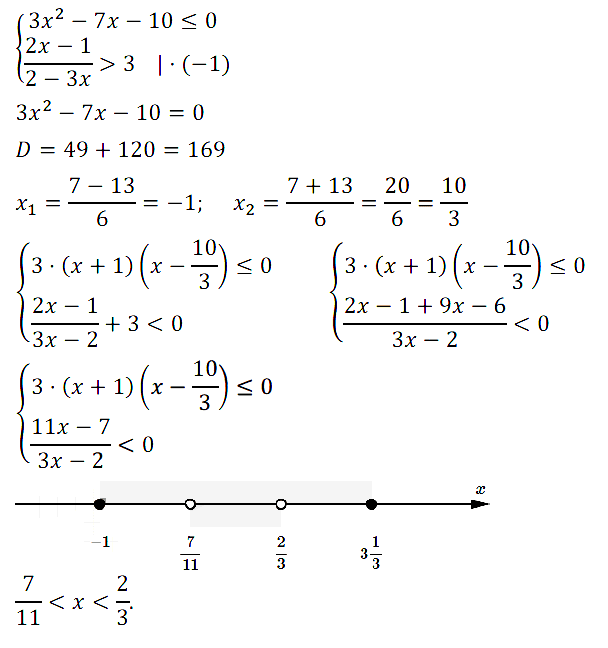
№ 9. Найдите длину отрезка, служащего решением двойного неравенства
2 ≤ (4x – 7)/5 ≤ 4. Укажите середину отрезка.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
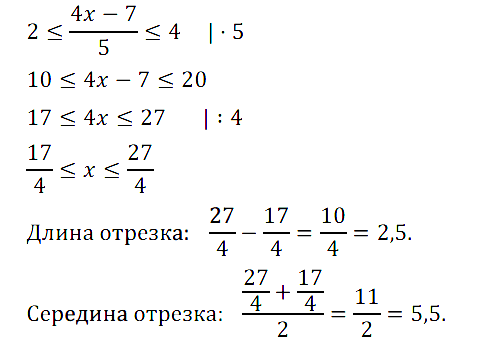
№ 10. Найдите все целые числа, удовлетворяющие системе неравенств
{ (х – 1)/2 – (2х + 3)/3 + x/6 < 2 – (х + 5)/2,
{ 1 – (х + 5)/8 + (4 – x)/2 < 3x – (x + 1)/4.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
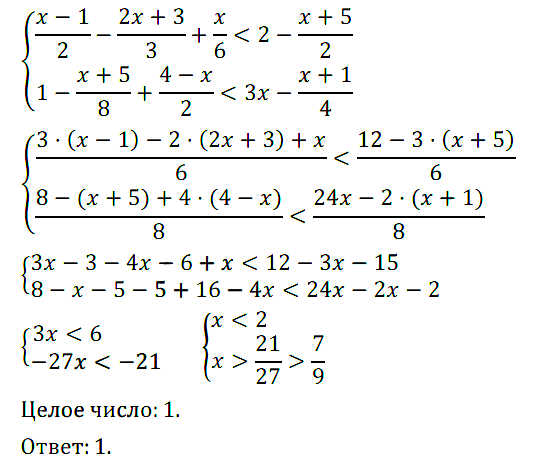
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 1. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ. Домашняя контрольная работа № 1 с ответами и решениями
Мордкович Алгебра 8 ДКР-1
Мордкович Алгебра 8 ДКР-1 — РЕШЕНИЯ и ОТВЕТЫ на домашнюю контрольную работу № 1 «Алгебраические дроби» из учебного пособия: «Алгебра 8 класс в 2 частях. Часть 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др. — М.: Мнемозина, 2014». Представленные ниже 2 варианта контрольной работы по алгебре 8 класса и ответы на нее ориентированы на задачник «Алгебра 8 класс» авторов А.Г. Мордкович и др.
Ответы на контрольную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Домашняя контрольная работа № 1
Типовые задания в ДКР № 1: 1) при каких значениях переменной алгебраическая дробь равна нулю, а при каких не существует? 2) Сократите дробь. 3) Найдите значение выражения. 4-6) Упростите выражение. 7) Найдите значение выражения.  Упростите выражения. 9) Докажите, что значение выражения … не зависит от значения входящих в него переменных. 10) Решите задачу, выделяя три этапа математического моделирования.
Упростите выражения. 9) Докажите, что значение выражения … не зависит от значения входящих в него переменных. 10) Решите задачу, выделяя три этапа математического моделирования.
Контрольная работа № 1. Вариант 2

Ответы на домашнюю контрольную № 1
«Алгебраические дроби»
Смотреть Решения и Ответы на Вариант № 1
Смотреть Решения и Ответы на Вариант № 2
Вы смотрели «Мордкович Алгебра 8 ДКР-1» — ГДЗ на контрольную работу № 1 «Алгебраические дроби» из учебного пособия: «Алгебра 8 класс в 2 частях. Часть 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др. — М.: Мнемозина, 2014». Представленные ниже 2 варианта контрольной работы по алгебре 8 класса и ответы на нее ориентированы на задачник «Алгебра 8 класс» авторов А.Г. Мордкович и др.
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Мордкович и др.)
Ученикам, которые хотят разобраться в дисциплине более тщательно, поучаствовать в конкурсе или олимпиаде, будет полезно применять решебник по алгебре за 7 класс в качестве вспомогательного, дополнительного материала. С этой целью семиклассникам стоит выработать схему занятий с учетом базового уровня и задач. Когда еще пригодятся ГДЗ за 7 класс? Решебники – это прекрасное решение в случае отсутствия на уроке из-за болезни, поездок на спортивные сборы или творческие конкурсы, а также для родителей и даже учителей, которым нужно быстро проверить задания.
Готовые ответы для учебника Мордкович, Александрова, Мишустина, Тульчинская
Уже в 9 классе придется сдавать экзамен по алгебре и именно на старте изучения дисциплины стоит основательно разбирать каждую тему, чтобы потом в быстром темпе нагонять пропущенный материал.
Дабы не пришлось часами просиживать над упражнениями, а удалось быстро изучить базовые алгоритмы решений даже самых сложных уравнений, выбирайте ГДЗ по алгебре за 7 класс, Мордковича. С наличием такого сборника подсказок родителям не придется тратить свое время и нервы на длительные разъяснения и проверку материала.
Семиклассникам со всеми трудностями при обучении поможет справиться уникальный решебник. Задания с разной сложностью собраны в учебнике от авторского коллектива Мордкович, Александрова, Мишустина, Тульчинская. В нем имеются задачи особой сложности, которые кажутся невыполнимыми.
Готовые решения для седьмого класса
ГДЗ по алгебре не только упростит обучение, но и поможет заинтересовать учеников предметом, ведь, если долго пытаться решить то, что не понимаешь, это утомляет и интерес теряется. Именно комплекс курса и решебника мотивирует разобраться даже в самых сложных темах, изучать числовые и алгебраические выражения, линейные функции, их графики и системы линейных уравнений.
Домашние задания с сервисом «Решалка» – это просто, быстро и эффективно. Можно воспользоваться с любого доступного гаджета. Не упустить ни единой темы и получать хорошие отметки Вы сможете с нашими онлайн-решебниками. Ждем Вас.
Авторы:
Изд-во:Мнемозина 2019-2020-2021
Вид УМК:задачник
Часть:1, 2
Топовые ГДЗ по другим предметам
Подробные решения по алгебре за 7 класс авторы Мордкович, Александрова, Мишустина
Иногда школьники, желающие разобраться в сути предмета глубоко и, например, поучаствовать в предметных конкурсах и олимпиадах, применяют онлайн справочник в качестве вспомогательного, дополнительного сборника. В этом случае семиклассники будут заниматься по ним на основе специальной схемы, учитывающей их базовый уровень, задачи и цели.
Кому еще будут полезны ГДЗ по алгебре за 7 класс Мордкович?
Помимо непосредственно учеников, в том числе – находящихся на домашней и семейной форме обучения, часто отсутствующих на уроках по болезни, из-за посещения спортивных сборов и творческих конкурсов, решебник по алгебре для 7 класса Мордкович регулярно используют:
- родители семиклассников, чтобы проконтролировать процедуру выполнения своими детьми домашних заданий, оценить уровень их знаний перед контрольными и проверочными по дисциплине;
- сами школьные учителя-предметники, чтобы проверить уровень знаний учеников, быстро осуществить контроль выполнения заданий – домашних и классных. Помощники в виде справочных материалов существенно сокращают время, необходимое на проверку тетрадей, высвобождая его на другие, не менее важные дела;
- репетиторы и руководители предметных кружков и курсов — для составления интересных заданий своим ученикам, а также для отслеживания порядка грамотной записи условия, вопроса и решения к каждому номеру в соответствии с действующими образовательными стандартами.
Удобные и практичные готовые решения по алгебре за 7 класс (авторы Мордкович А. Г, Александрова Л. А. и Мишустина Т. Н.) имеют множество преимуществ. Среди основных, отмечаемых пользователями таких материалов:
- их доступность в постоянном режиме – 24 часа в день, ежедневно;
- грамотно организованный поиск, позволяющий найти нужное решение не только по фамилии автора пособия и названию учебного материала, но и по темам, параграфам, страницам;
- возможность сэкономить семейный бюджет, отказавшись или значительно снизив расходы на репетиторов и курсы по дисциплине.








